Метод главных компонентов

Метод главных компонентов используется при рассмотрении некоторого множества случайных значений показателей Y_i, i = 1, 2, 3, ..., k в целях определения общих для них факторов (компонентов), от которых все они зависят. Степень зависимости i-го показателя от j-го компонента отражается величиной а_ij, называемой нагрузкой i-го показателя на j-й компонент.

Результатом анализа является модель главных компонентов, в которой каждый показатель представлен суммой произведений компонентов и их нагрузок:

,

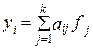где f_j - центрированные, нормированные и некоррелированные компоненты (случайные величины f₁ и f₂называются некоррелированными, если коэффициент их корреляции равен нулю; случайная величина называется центрированной, если ее математическое ожидание равно нулю; центрированная случайная величина называется нормированной, если ее дисперсия равна единице). Модель главных компонентов показывает, что и в какой степени определяет исследуемые показатели, а также объясняет связи между ними (см. [6.21; 6.28]).

Факторный анализ

Факторный анализ по своей сути совпадает с методом главных компонентов, однако позволяет представить показатели через меньшее количество факторов (компонентов), поэтому используется при исследовании сложных систем управления, с большим числом показателей и сложными взаимосвязями между ними (см. [6.44]).

Предполагается, что за множеством показателей системы стоит небольшое число независимых скрытых параметров, называемых факторами. Они определяют значения показателей и взаимосвязь между ними. Степень взаимосвязи между фактором и показателем описывается факторной нагрузкой, количественное значение которой равно коэффициенту корреляции между ними. Если фактор связан со всеми показателями, то он называется генеральным, если с некоторой группой, то групповым, и наконец, если существует связь только с одним показателем, то фактор называется специфическим.

Следовательно, показатели, имеющие высокую нагрузку на общий фактор, обладают общим свойством, которому можно дать название, исходя из физического смысла данной группы показателей. Процедура факторного анализа состоит в переходе от высокоразмерного пространства, выраженного матрицей {у_ij},(i = 1, 2, 3, ..., k, j = 1, 2, 3, ..., n) значений i-х показателей в j-x экспериментах (наблюдениях), к низкоразмерному факторному пространству {г_ij}, (i = 1, 2, 3, ..., k; j = 1, 2, 3, ..., т; т < п, т = т(п)), описываемых для i-х показателей.