Приборы для ориентирования на местности

При ориентировании на местности для измерения магнитных азимутов и магнитных румбов пользуются буссолями (рис.5, а) и компасами (рис. 5, 6).

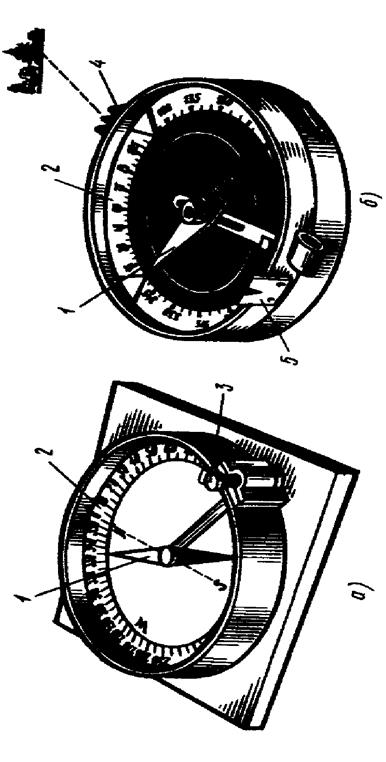
Главные части буссоли или компаса — магнитная стрелка 1, вращающаяся на острие шпиля, и кольцо 2 с угловыми делениями. Северный конец стрелки делают темно-синим или вороненым. В за­висимости от того, как подписаны деления, различают азимуталь­ное и румбическое кольца. В азимутальном кольце деления подпи­сывают против направления движения часовой стрелки от 0 до 360°, в румбическом — на концах нулевого диаметра ставят нули, пер­пендикулярного ему диаметра — 90°. В нерабочем состоянии стрел­ка приподнята на шпиле и прижата к защитному стеклу арретиром 3.

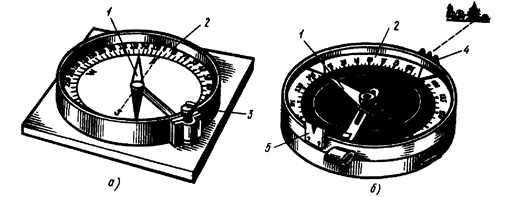Рис.5. Приборы для ориентирования по магнитным меридианам:

а — буссоль, б — компас; 1 — стрелка, 2 — кольцо, 3 — арретир, 4,5 — диоптры

Буссоли бывают штативные, устанавливаемые при измерени­ях на штатив; ручные, теодолитные, устанавливаемые на угломер­ные приборы — теодолиты; настольные, укладываемые на карту или план при их ориентировании. Настольная буссоль(рис.5, а) называется ориентир-буссолью.

Штативные, ручные буссоли и компасы имеют приспособление для визирования — наведения на точку линии, азимут которой измеряется. Простейшие виды таких приспособлений — диоптры: глазной 5 и предметный 4. В буссолях линия, соединяющая середи­ны диоптров, постоянно совпадает с нулевым диаметром кольца; в компасах диоптры крепятся на вращающейся крышке.

Принцип измерения азимута линии буссолью заключается в том, что нулевой диаметр буссоли совмещают с направлением этой линии, а по северному концу магнитной стрелки отсчитывают зна­чение азимута или румба. Например, на рис. 2.5, а такой отсчет равен 335°05'.

В компасе с подвижными диоптрами совмещают северный конец стрелки с нулем кольца, а линию диоптров — с направлением опре­деляемой линии и по указателю предметного диоптра отсчитывают значение азимута данной линии.

Для определения истинного азимута применяют гиротеодолит, сочетающий в себе гироскоп как датчик направления географичес­кого меридиана и измеритель углов — теодолит. Гироскоп пред­ставляет собой вращающееся устройство, подобное волчку, главная ось которого под действием суточного вращения Земли и силы тяжести всегда занимает положение, параллельное оси вращения Земли, т. е. в плоскости географического меридиана.

4. Прямая и обратная геодезические задачи

В системе плоских прямоугольных координат многие геоде­зические расчеты основаны на формулах решения прямой и об­ратной геодезических задач.

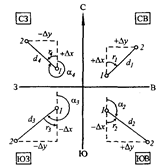
В прямой геодезической задаче известны горизонтальное проложение d прямого отрезка 1—2 (рис. 6), его дирекционный угол α, координаты х₁ и у₁ начальной точки 1. Требуется вычис­лить координаты х₂, у₂, точки 2.

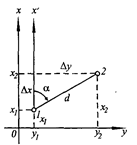Рис. 6. Прямая и обратная геодезические задачи Рис. 7. Знаки приращений координат, дирекционные углы и румбы

в различных четвертях

Сначала вычисляются приращения координат:

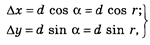(1)

а затем искомые координаты:

х₂ = х₁ + Δх

у₂ = у_{1 +} Δу (2)

Знак приращения координат Δх и Δу зависит от направления отрезка 1—2 (рис.7) и соответствует знаку cos α и sin α. При вычислениях с использованием румба r значениям Δх и Δу при­писывают знак "плюс" или "минус".

Пример 1. Вычислить координаты точки 2 х₂ и у₂ , если дли­на линии 1—2 d_1-2 = 100,00 м, дирекционный угол α_1-2 = 125° 20', координаты точки 1 х₁= 500,00 м, у₁ = 1000,00 м.

Решение. Для вычисления используют румбы или дирекционные углы. Найдем вначале румб r_1-2 = ЮВ : (180° — α_1-2) = ЮВ : 54° 40', а затем Δx = 100,00 · cos 54° 40' = 57,83 м;

Δy = 100,00 · sin 54° 40' = 81,58 м. Определив знак Δx и Δу, по формуле 2 вычислим x₂ и у₂ :

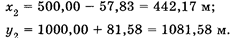
В обратной геодезической задаче по известным координатам х₁ и y₁, x₂ и y₂ конечных точек отрезка прямой 1—2 (см. рис.6) вычисляют горизонтальное проложение d, румб r_1-2 и дирекци­онный угол α_1-2.

Вначале вычисляют тангенс румба:

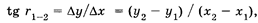(3)

а затем численное значение румба: r = arc tg (Δу/Δx).

По знакам разностей у₂ — у₁ и x₂ — х₁ определяют название четверти румба (см. рис.7) и вычисляют дирекционный угол α (см. табл.1). Длину отрезка 1—2 находят по следующим фор­мулам:

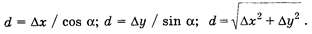(4)

Пример 2. Вычислить длину d_1-2 и дирекционный угол α_1-2 линии 1—2, если известны координаты точек 1 и 2:

х₁ = 200,00 м; у₁ = 400,00 м, х₂ = 286,34 м и y₂ = 349,54 м.

Решение. По формуле (3) рассчитаем

tg r_1-2 = (349,54 - 400,00) / (286,34 - 200,00) = -50,46/+86,34 = - 0,58443, а также

arc tg (Δу/Δx)= - 30,30° = - 30° 18,1'. По знакам +Δх_1-2 (северное направление), - Δу_1-2 (западное направле­ние) найдем r_1-2 = СЗ : 30° 18,1', а дирекционный угол α_1-2= 360° - r_1-2 = 329° 41,9'.

По формулам (4) вычислим d_1-2 = 86,34 / cos 329° 41,9' = 100,00 м;

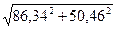d_1-2 = - 50,46 /sin 329° 41,9' = - 50,46 /(- 0,50458) = 100,00 м;

d_1-2 = = 100,00 м.