ДЕФОРМАЦИИ ОБОЛОЧЕК

ОБОЛОЧКИ. ИХ КЛАССИФИКАЦИЯ.

5.1. Основные понятия теории оболочек. Виды оболочек.

Оболочкой называется тонкостенная пространственная конструкция, тело которой образовано при движении короткого прямолинейного отрезка, средняя точка которого остаётся на гладкой поверхности, а направление - перпендикулярным к поверхности (рис. 5.1).

Длина отрезка характеризует толщину 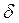оболочки. Если длина сохраняется постоянной, то оболочка обладает постоянной толщиной; в противном случае – переменной.

Поверхность, на которой располагаются средние точки прямой, называется срединной поверхностью оболочки.

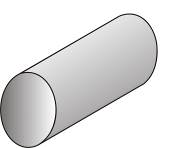
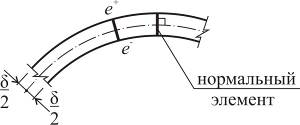
Рис. 5.1

Поверхности, очерчиваемые концами элемента, остаются гладкими.

Контур оболочки или боковую грань можно определить как след скольжения нормали по замкнутой линии на срединной поверхности. Оболочки могут иметь не один, а два и более контура (оболочки с отверстиями). Оболочка может и не иметь контура вовсе, например замкнутая сферическая оболочка в виде полого шара или в форме тора. Оболочка по контуру обычно подкрепляется различными конструктивными элементами в виде балок, арок, ферм, сплошных дисков (диафрагм). На рис. 5.2 показано несколько примеров таких оболочек, в частности пологие оболочки с бортовыми элементами в виде арок и ферм и ребристая цилиндрическая оболочка, подкреплённая стрингерами.

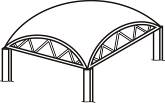
Рис. 5.2

Многообразие форм оболочек, состоящее в различии толщин и габаритных размеров, влечёт за собой возможность упрощения (схематизации) действительной работы тонкостенной конструкции. Эта идеализация формулируется в форме гипотез, аналогичных по природе гипотезам теории расчёта стержней или пластин. По существу, формулировка гипотез для оболочек отличается от предпосылок для пластин лишь употреблением термина «поверхность оболочки» вместо «плоскость пластинки» на соответствующих местах (см. раздел 1 п. 1.2 и п. 5.5). Введение гипотез существенно упрощает расчёт оболочек по сравнению со строгой теорией. Например, если в теории оболочек при выводе уравнений состояния пренебрегают всеми слагаемыми, имеющими порядок 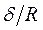по сравнению с единицей ( 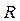- радиус кривизны срединной поверхности), то оболочки относятся к категории тонких. Количественно это отношение составляет:

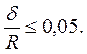(5.1)

Оболочки с указанным ограничением широко применяются в строительстве. Раздел строительной механики, в котором они изучаются, известен как техническая или геометрически линейная теория расчёта оболочек.

Помимо тонких оболочек в литературе рассматриваются также толстые оболочки и оболочки средней толщины.

По форме срединной поверхности оболочки могут быть Ццилиндрическими, коническими и т. п. Материалом оболочек может служить дерево, металл, железобетон, их сочетание.

Оболочки применяются в промышленном и гражданском строительстве – в качестве несущих конструкций покрытий и перекрытий, козырьков над входами зданий, трибунами стадионов и пр.; в тоннелестроении, в частности – в метро; в судо – и самолётостроении – корпуса судов, доков, фюзеляжи и крылья самолётов; в машиностроении – кузова автомобилей, цистерны для перевозки жидкостей, бункера и т . п. (рис. 5.3,а).

Во многих случаях оболочки подкрепляют рёбрами в одном или двух направлениях (шпангоуты и стрингеры). Оболочки могут иметь отверстия, люки, или, наоборот, утолщения в некоторой области (рис. 5.3,б).

а б

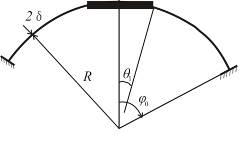
Рис. 5.3

5.2. Формы описания поверхностей оболочек

Срединная поверхность оболочки может быть задана уравнением:

как в явном 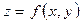, (5.2)

так и в неявном виде

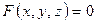, (5.3)

где 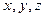- координаты срединной поверхности оболочки, 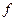, 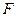- непрерывные функции переменных .

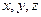Примерами подобного способа описания поверхности служат уравнения параболоида и сферы (рис. 5.4,а, б):

,

.

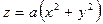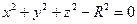а б

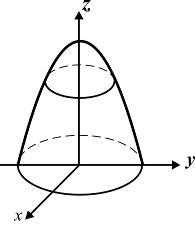
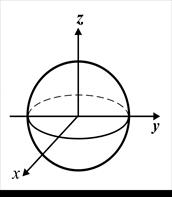
Рис. 5.4

Уравнение поверхности может быть задано и в параметрической форме:

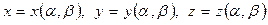, (5.4,а)

где 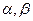- параметры срединной поверхности оболочки (рис. 5.5); очевидно, в векторном виде оно записывается немного короче, а именно:

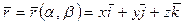. (5.4,б)

В качестве параметров 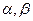могут быть приняты криволинейные координаты сетки координат, нанесённой на срединной поверхности оболочки.

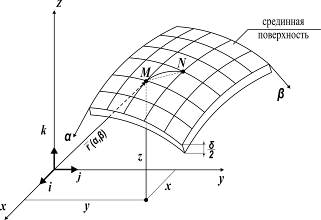
Рис. 5.5

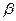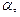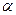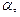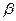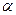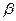Фиксируя на поверхности значение одной из координат, например , и изменяя можно провести линию . Аналогично, если оставить постоянным значение а менять , то нетрудно провести другую линию. Линии семейств и образуют координатную сетьна поверхности.

Любая точка на поверхности характеризуется координатами принятой сетки. Если в точке М восстановить нормаль к поверхности, то плоскость, содержащая нормаль, называется нормальной (рис. 5.6,б).

В общем случае система криволинейных координат выбирается произвольно. Единственное ограничение – координатные линии не должны касаться друг друга в рассматриваемой области поверхности; это означает, что 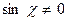, где 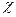- угол между линиями 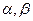. Для упрощения записи основных уравнений теории оболочек следует пользоваться ортогональными криволинейными координатами, для которых нормали, проведённые в соседних с М точках 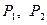, пересекают нормаль в самой точке М. Отрезки 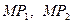являются радиусами кривизн 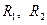соответствующих координатных линий; величины, обратные к ним, называются кривизнами

линий 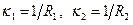. Доказано, что среди множества координатных сетей существует такая сеть, для которой кривизны одной группы координатных линий принимают минимальное, а другой – максимальное значение; координатные линии с указанным свойством называются линиями главных кривизн. Произведение главных кривизн называется гауссовой кривизной поверхности оболочки .

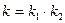В зависимости от величины и знака гауссовой кривизны оболочки делятся на три класса. К первому относятся оболочки с нулевой кривизной (оболочки, у которых кривизна в направлении одной из координат равна нулю). К этому классу принадлежат цилиндрические и конические оболочки (рис. 5.6,а). Второй класс образуют оболочки двоякой кривизны. Среди них следует различать выпуклые оболочки ( 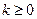) (рис. 5.4, рис. 5.6,б) и вогнуто-выпуклые ( 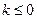) (рис. 5.6,в). Особый класс составляют призматические оболочки – складки (рис. 5.6,г).

а б

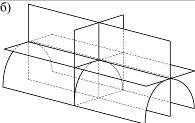
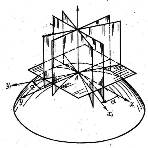
в г

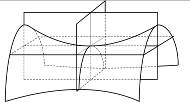
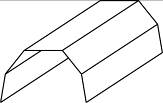
Рис. 5.6

5.3. Геометрические характеристики срединной поверхности.

Условия Кодацци - Гаусса

Для описания геометрии поверхности следует обратиться к бесконечно малому элементу, выделенному на поверхности оболочки двумя координатными линиями 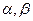у точки М (см. рис. 5.5). Пусть другая точка N находится на бесконечно малом расстоянии 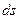от точки М. Этот бесконечно малый отрезок МN называется линейным элементом. Несмотря на такое название, его следует изображать в виде кривой линии, т. к. поверхность оболочки, на которой показана линия, криволинейная (рис. 5.7,а).

а б

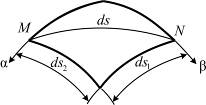
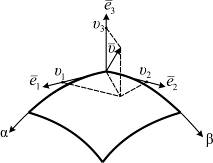
Рис. 5.7

Квадрат длины этого элемента в ортогональных криволинейных координатах равен:

,

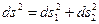где 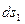, 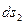- длины линейных элементов, взятых вдоль координатных линий, которые можно выразить через приращения криволинейных координат 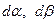с помощью коэффициентов А и В,

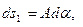
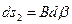. (5.5)

Тогда выражение для квадрата линейного элемента принимает вид

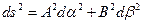. (5.6)

Величины 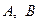называются коэффициентами или параметрами Ламэ.

Линейный элемент поверхности можно представить как приращение радиуса – вектора 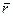при переходе из точки М в точку N

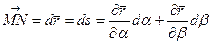. (5.7)

Векторы 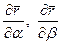, характеризующие «скорость роста» радиуса – вектора 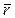в каждой точке поверхности, направлены вдоль касательных к соответствующим координатным линиям 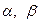. Квадрат длины линейного элемента согласно (5.7) равен:*

.

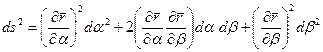Если линии 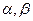ортогональны, то второе слагаемое последнего выражения равно нулю; и тогда

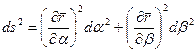. (5.8)

Сравнивая (5.6) и (5.8), можно заключить, что параметры Ламэ равны производным радиуса – вектора 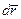по криволинейным координатам:

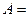
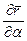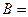
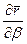, . (5.9)

На основе (5.4,б) они могут быть выражены через декартовы координаты:

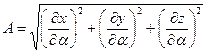, (5.10,а)

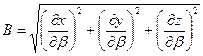. (5.10,б)

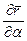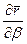Отсюда следует, что величины А и В равны модулям векторов производных и . С позиций кинематики А и В – «модули скоростей изменения» радиуса – вектора 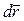произвольной точки поверхности оболочки по направлениям криволинейных координат .

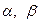В дальнейшем при выводе условий совместности деформаций понадобятся т. н. условия Кодацци, которые связывают параметры Ламэ с главными радиусами кривизны, а именно:

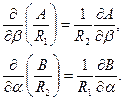(5.11,а)

Для доказательства данных соотношений, обеспечивающих сплошность (непрерывность) поверхности оболочки, необходимо обратиться к определениям единичных векторов нормированного координатного базиса, т. е. к ортам (рис. 5.7):

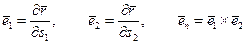
и подставить в них (5.5). В результате подстановки единичные орты в направлениях координатных линий находятся по формулам:

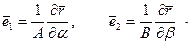
Любой вектор, в частности вектор перемещений точки срединной поверхности оболочки 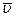, может быть представлен в этом координатном базисе разложением

,

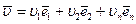где 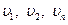- проекции вектора перемещений на орты (рис. 5.7,б).

Производная вектора 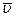вычисляется как производная сложной функции, т. е.

.

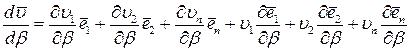Производные единичных орт находят по формулам:

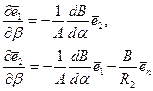
и т. п.*

Условия Кодацци выводятся непосредственно из очевидного равенства

. (*)

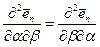Раскрывая его с помощью определений производных орта :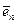

,

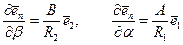приходят к новому равенству

.

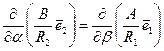Выполнив теперь дифференцирование произведений, стоящих в скобках,

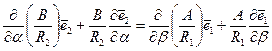
и подставив сюда известные формулы для производных орт:

,

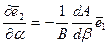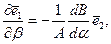
после группировки слагаемых, нетрудно установить соотношение

= ,

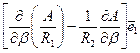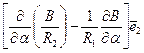которое можно переписать в форме уравнения

.

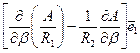
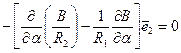Выражения в квадратных скобках полученного уравнения можно считать проекциями некоторого нулевого вектора, представленного своим разложением по ортам. В таком случае проекции вектора равны нулю. Поэтому множители перед ортами 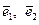равны нулю. Следовательно, должны выполняться следующие равенства:

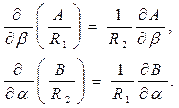(5.11)

Это и есть условия Кодацци.

Помимо условий Кодацци, являющихся следствием равенства (*), при регулярности* формы поверхности должны соблюдаться ещё два равенства аналогичного вида

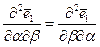и .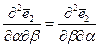

Раскрывая первое из этих равенств с помощью известных определений производных орта 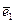, приходят к более подробной записи равенства

.

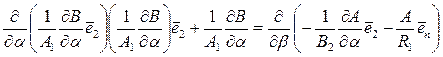Выполнив здесь дифференцирование, равенство можно представить в форме уравнения

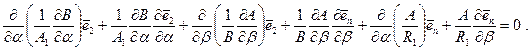
С учётом определений производных ортов после группировки слагаемых векторное уравнение принимает вид

. (**)

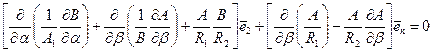Отсюда следует, что проекции некоего вектора на орты равны нулю, а это приводит к скалярному равенству

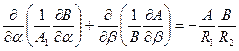. (5.12)

известному в геометрии как условие Гаусса.

Вторая проекция (множитель, стоящий перед 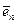в уравнении (**)), очевидно, является условием Кодацци.

Равенство 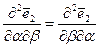не даёт ничего нового; оно может быть использовано для проверки полученных ранее условий Кодацци – Гаусса. Таким образом, при существовании (регулярности) срединной поверхности должны удовлетворяться условия Кодацци – Гаусса для четырёх функций .

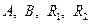5.4 Параметры Ламэ для поверхности оболочки вращения

Чтобы уточнить представление о параметрах Ламэ, в этом подразделе приводится их вычисление для поверхности оболочки вращения. Срединная поверхность оболочки вращения, как известно, образуется путём вращения произвольной кривой вокруг какой – либо оси, например оси Оz (рис. 5.8,а).

а б

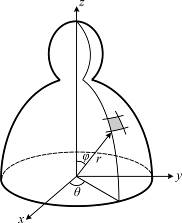
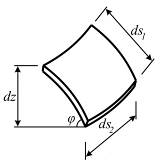
Рис. 5.8

В цилиндрической системе координат поверхность оболочки вращения описывается тремя уравнениями:

.

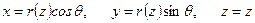Если из оболочки вырезать элемент, ограниченный двумя параллельными плоскостями, перпендикулярными оси вращения, и двумя меридиональными плоскостями с углом 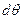, проходящими через ту же ось (рис. 5.8,б), то длина элемента вдоль окружности определяется по формуле

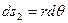. (5.12,а)

А длина в другом направлении

,

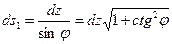где 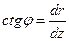. Следовательно,

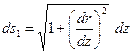. (5.12,б)

Очевидно, положение нормали в любой точке поверхности определяется направляющими косинусами:

, .

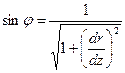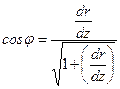Квадрат линейного элемента поверхности оболочки с учётом определений (5.12) равен:

.

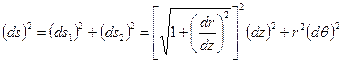Таким образом, величины коэффициентов Ламэ оболочки вращения согласно (5.6) равны:

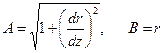. (5.13)

Если поверхность оболочки вращения рассматривается в другой системе координат, например в сферической, то параметры Ламэ принимают иные выражения. В частности, на основе уравнения поверхности оболочки вращения в сферической системе координат

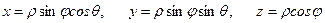
коэффициенты Ламэ имеют вид:

,

.

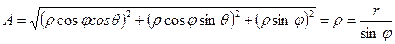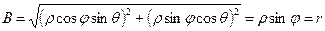5.5. Основные гипотезы технической теории расчёта оболочек

В технической теории расчёта оболочек, как и пластин, приняты те же гипотезы о распределении напряжений и деформаций.

I. Статическая гипотеза – нормальные напряжения, возникающие при деформировании вследствие взаимного нажатия горизонтальных слоёв оболочки друг на друга, на площадках, параллельных срединной поверхности, принимаются нулевыми .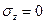

Это означает, что бесконечно тонкий слой оболочки находится в условиях плоского напряжённого состояния. К тому же и касательные напряжения 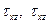относятся к второстепенным. Они также принимаются равными нулю.

II. Кинематическая гипотеза – прямая, перпендикулярная срединной поверхности в начальном положении, остаётся перпендикулярной к поверхности и в деформированном состоянии (гипотеза прямых нормалей Кирхгофа) (рис. 5.9). Эта гипотеза, по существу, вытекает из первого предположения. Действительно, из условия отсутствия касательных напряжений 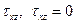(в условиях плоского напряжённого состояния) следует, что .

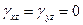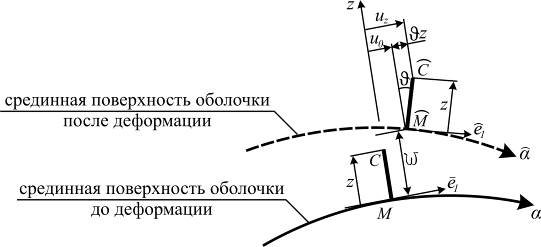
Рис. 5.9

Поскольку нормальные напряжения 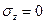, то деформации срединной поверхности, согласно физическим соотношениям теории упругости, находят по формулам [4]:

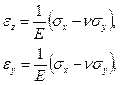(5.14)

,

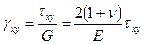где 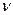- коэффициент Пуассона.

Отсюда определяется обратная зависимость напряжений от деформаций:

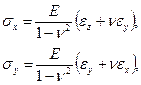(5.15)

.

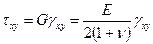На основании первой гипотезы

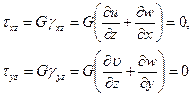
можно видеть, что

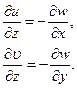
Интегрируя последние соотношения с учётом граничных условий на срединной поверхности оболочк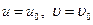и ( при 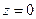), легко установить характер изменения перемещений точки С, взятой на некотором удалении 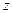от поверхности (см. рис. 5.9), а именно:

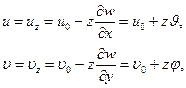(5.16)

где 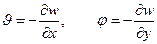- углы наклона нормали СМ с осями триэдра, расположенными в касательной плоскости.

В следующем подразделе приводится иной вывод формул для перемещений произвольной точки оболочки, исходя из рассмотрения геометрической картины деформирования (рис. 5.10).

5.6 Определение перемещений оболочек

Уравнение срединной поверхности оболочки в начальном состоянии записывается в виде

.

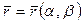В деформированном состоянии положение произвольной точки М срединной поверхности можно определить через радиус – вектор

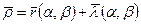, (5.17)

где

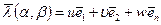(5.18)

- вектор перемещений точки оболочки, представленный компонентами 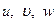по направлениям осей триэдра 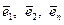(см. рис. 5.10).

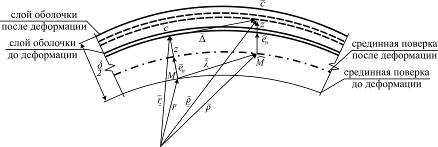
Рис. 5.10

Пусть 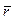обозначает радиус – вектор точки С, отстоящей от срединной поверхности на расстоянии z . Очевидно,

.

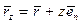Согласно гипотезе Кирхгоффа – Лява

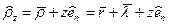
где 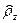- радиус – вектор той же точки после деформирования (точки 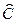), 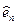- единичный вектор нормали к деформированной поверхности, связанный с двумя другими ортами известным соотношением *.

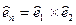Принимая во внимание последние зависимости, вектор перемещения 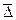любой точки оболочки при деформировании можно выразить через перемещение её проекции на срединную поверхность в следующем виде:

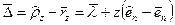. (5.19)

Чтобы перейти к координатной форме записи рассматриваемого вектора перемещений, следует выполнить несложные преобразования. Сначала, пользуясь определением единичного вектора

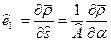, (5.20)

который направлен по касательный к координатной линии 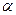на деформированной срединной поверхности, и зависимостями (5.17) и (5.18), легко установить, что

.

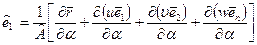Здесь

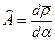(5.21)

- коэффициент Ламэ деформированной срединной поверхности, квадрат которого, согласно определению (5.9), равен скалярному произведению производной

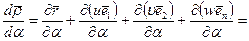
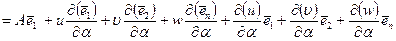
на саму себя. Принимая во внимание правила вычисления производных единичных векторов, в частности**

,

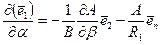выражение для производной можно записать в следующем виде:

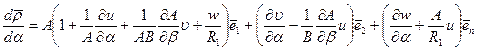. (5.21)

Составив скалярное произведение 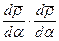и пренебрегая в нём величинами второго порядка малости, находят

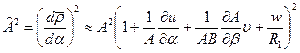. (5.22)

При выводе данной формулы принято во внимание свойство ортогональности единичных векторов .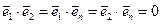

С помощью выражений (5.21), (5.22) единичный орт 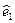на деформированной срединной поверхности (см. 5.20) можно выразить через тот же орт в начальном состоянии

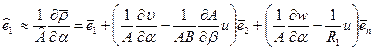. (5.23,а)

Аналогично находится и орт другого направления, т.е.

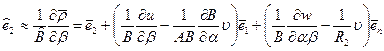. (5.23,б)

Умножая векторно один орт на другой и пренебрегая членами второго порядка малости, вычисляют орт нормали в деформированном состоянии срединной поверхности

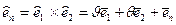. (5.24)

Здесь введены обозначения величин

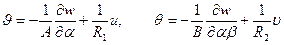, (5.25)

смысл которых выяснится немного позже. При деформировании оболочки вектор перемещения любой точки, удалённой от срединной поверхности на отрезок z, теперь, согласно (5.19) и (5.24), можно определить с помощью величин 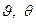в виде

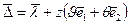. (5.26)

Проектируя полученное векторное равенство на оси триэдра, выводят формулы для определения перемещений любой точки оболочки в скалярной форме:

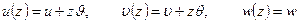. (5.27)

Отсюда вытекает, что величины 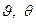являются проекциями орта нормали 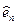на оси 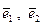. В силу малости перемещений эти проекции равны углам 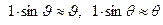, на которые поворачивается нормаль 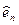вокруг осе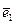й и 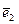. Следовательно, величины 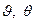есть не что иное, как углы поворота нормали к срединной поверхности по направлениям координатных линий поверхности оболочки.

Из сравнения формул (5.27) с аналогичными выражениями для перемещений пластин:

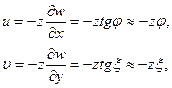
где 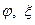- углы наклона нормали к срединной поверхности пластинки с осями координат (см. раздел 1), следует, что, в отличие от пластин, перемещения в оболочках, естественно, зависят от формы поверхности оболочки.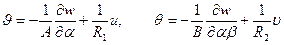

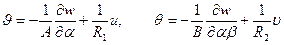
5.7 Деформации оболочек

Длины линейных элементов, взятых вдоль координатных линий, на начальной поверхности оболочки равны:

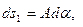
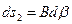, (5.28,а)

где 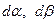- приращения криволинейных координат (рис. 5.11).

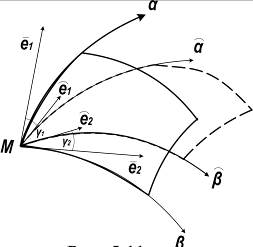
Рис. 5.11

После деформирования линейные элементы удлиняются

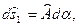
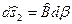. (5.28,б)

Здесь 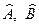- коэффициенты Ламэ (5.21) на деформированной срединной поверхности.

Относительное удлинение в направлении координатной линии 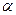обозначается

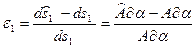. (5.29)

Согласно определению длины элемента в направлении линии 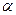до и после деформирования (5.28), его деформация в этом направлении с учётом равенства (5.22) выражается через перемещения по формуле

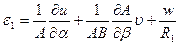. (5.30,а)

Очевидно, квадрат коэффициента Ламэ (5.22) на деформированной срединной поверхности теперь можно представить в виде

,

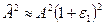откуда вытекает зависимость между коэффициентами Ламэ в начальном и деформированном состоянии оболочки

.

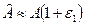Аналогично определяется деформация линейного элемента оболочки вдоль линии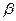

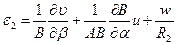(5.30,б)

и соответствующий параметр Ламэ

.

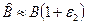Сдвиг элемента срединной поверхности оболочки, по определению, равен сумме углов 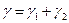(рис. 5.11).

Так как углы 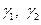малы, то 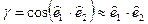. Подставив сюда выражения (5.23) для единичных векторов для деформированного положения оболочки, находят деформации сдвига

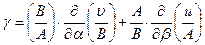. (5. 31)

Теперь можно перейти к выводу формул для кривизны элемента слоя оболочки, расположенного параллельно срединной поверхности и удалённого от неё на одинаковом расстоянии z*. Если, в частности, рассматривать нормальное сечение оболочки плоскостью, проведённой через касательную к координатной линии 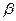, то можно увидеть, что кривая линия 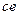, являющаяся сечением слоя, подобна кривой 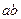, взятой на срединной поверхности (рис. 5.12).

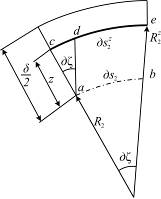
Рис. 5.13

Очевидно, радиусы кривизн эквидистантного слоя вдоль координатных линий отличаются от соответствующих радиусов срединной поверхности на отрезок z

. (5.32)

Второе равенство аналогично первому и относится к радиусу кривизны слоя в направлении линии .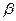

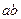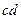Очевидно, отрезкам и координатной линии 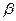, расположенным между двумя нормалями к срединной поверхности, соответствует одинаковое приращение координаты 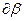; следовательно, длина линейного элемента равна

.

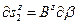Аналогично, и для линейного элемента линии другого направления (по линии 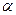) - 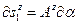. Здесь 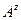, 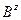- параметры Ламэ эквидистантного слоя оболочки.

Длины линейных элементов можно выразить и через радиусы кривизн, составив равенства:

,

где - центральные углы дуг элементов. После подстановки углов в выражения для длин приходят к новым определениям длин элементов: .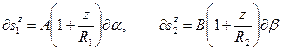

Сравнивая полученные выражения длин с их первоначальными определениями, выводят зависимость между параметрами Ламэ на срединной поверхности и в эквидистантном слое оболочки:

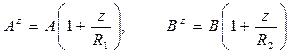. (5. 33)

Чтобы ввести понятие и определить величину кривизны оболочки при деформировании, необходимо обратиться к рассмотрению деформаций эквидистантного слоя по направлениям координатных линий. Их значения можно определить на основе формул, аналогичных (5.30) (для удлинений срединной поверхности). В частности, для деформации слоя вдоль линии 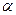можно составить формулу

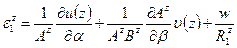, (5.34)

используя выражения для перемещений согласно (5.30) и параметры Ламэ - (5.33) для эквидистантного слоя. Выполнив необходимые операции по подстановке и дифференцированию, после группировки слагаемых с учётом условий Кодацци (5.11) выводят формулу для удлинения элемента слоя вдоль координатной линии 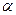, содержащую параметр деформаций срединного слоя:

.

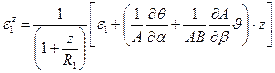Обозначив величину, стоящую в круглых скобках этой формулы, через

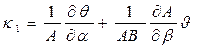(5.35а)

деформацию элемента можно представить более компактно

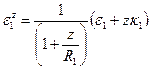(5.36,а)

и к тому же в виде, похожем на известную из курса сопротивления материалов запись деформации слоя изначально криволинейной балки. Отсюда вытекает, что величина 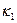определяет кривизну слоя оболочки, отстоящего на расстоянии 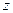от срединной поверхности, в направлении линии .

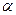Аналогично определяется деформация слоя и вдоль координатной линии :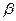

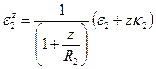, (5.36,б)

где кривизна 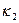вычисляется по формуле

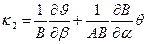. (5.35,б)

Подобным образом находят также деформации сдвига элемента эквидистантного слоя, выраженные через перемещения срединной поверхности (рис. 5.11):

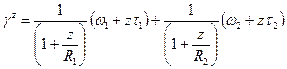. (5.37)

Для сокращения записи здесь введены новые параметры, характеризующие сдвиг элемента, а именно[1]:

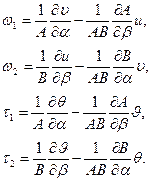(5.38)

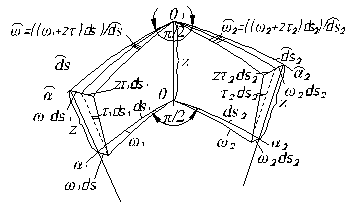
Рис. 5.14

Если воспользоваться определением деформаций сдвига срединной поверхности согласно (5.31), то с помощью параметров 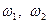их можно выразить более кратко, а именно:

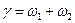, (5.39)

тем самым раскрыв геометрический смысл величин 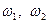, которые, очевидно, являются углами сдвига 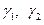элемента, взятого на срединной поверхности.

Составив суммы 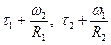, легко убедиться в их тождестве и потому обозначить их одним и тем же символом, например буквой

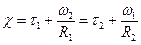. (5.40)

Этот параметр можно использовать для определения деформации параллельного слоя согласно (5.37) в следующей форме:

.

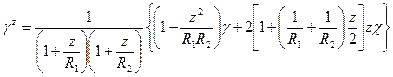Пренебрегая здесь членами порядка 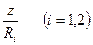по сравнению с единицей, легко установить, что деформации сдвига параллельного слоя равны:

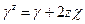. (5.41)

В соответствии с определением (5.40), величина 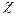при использовании выражений для 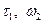по (5.38) может быть выражена через углы :

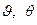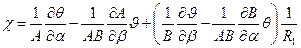. (5.42)

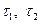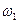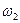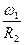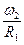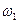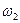Каков же смысл этой величины? Анализ структуры формулы (5.40) говорит о том, что каждое служит добавкой к значениям углов и , отнесённым к радиусам кривизн координатных линий другого направления, т. е. к величинам , , соответственно. Сами же углы и , согласно (5.39), являются углами сдвига взаимно перпендикулярных кромок элемента срединной поверхности (рис. 5.14). Отнесённые к радиусам кривизны, они, с позиций геометрии, очевидно, не что иное как кривизны. Следовательно, величины 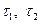тоже характеризуют кривизны. Тщательный анализ формулы (5.42) показывает, что величина 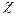характеризует деформацию кручения элемента срединной поверхности оболочки. Схема деформаций сдвига элементарного объёма оболочки может быть проиллюстрирована на примере деформаций куба (рис. 5.15,а).

а б

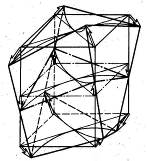
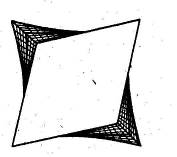
Рис. 5.15

Очевидно, каждая из сумм 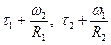, т. е. величина 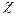, определяет относительный крутильный поворот противоположных кромок элемента. При этом две угловые точки контура срединной плоскости, расположенные по концам одной из диагоналей квадрата, опускаются, а две другие – поднимаются. Сама срединная плоскость искривляется. Вследствие того, что вертикальные ребра куба как нормальные элементы должны оставаться нормальными к искривленной срединной плоскости, неизбежен их поворот: два противоположных по диагонали ребра поворачиваются, сближаясь верхними концами, а два других – нижними. В результате этого по мере удаления от срединной плоскости происходит рост сдвига параллельных слоёв; в срединном же слое сдвиг отсутствует.

Общее представление о характере деформирования куба даёт картина, изображённая на рис. 5.15,б [11].

5.7. Условия геометрической совместности

деформаций оболочек

Параметры деформаций в каждой точке срединной поверхности, определяемые шестью формулами, являются функциями трёх независимых аргументов - перемещений оболочк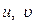и и :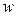

· ,

· ,

· ,

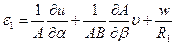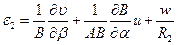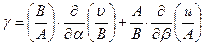(5.43)

· ,

· ,

· .

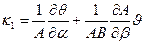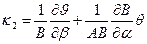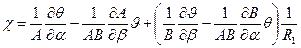Первые три компоненты деформаций ( 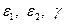) называются тангенциальными или мембранными. Они характеризуют степень растяжения (сжатия) и сдвига срединной поверхности оболочки. Параметры 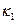, , 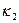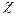называются параметрами изгибной деформации срединной поверхности. С их помощью можно установить деформации растяжения и сдвиги, которые возникают в эквидистантном слое.

Так как поверхность оболочки при деформировании сохраняется сплошной (разрывы или складки срединной поверхности недопустимы), то функци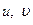и и 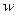должны быть непрерывными. Этого нельзя утверждать относительно деформаций 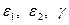и кривизн 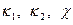. Однако параметры деформаций 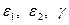, , 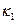, 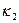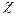должны удовлетворять определённым зависимостям, обеспечивающим сплошность (непрерывность) срединной поверхности. Указанные зависимости, как и в теории упругости, называются условиями совместности деформаций; их три. Они могут быть получены путём исключения перемещени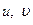й и 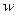из выражений для деформаций (5.43). Ниже они приводятся:

·

·

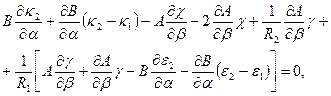
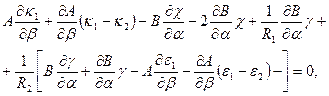
(5.44)

·

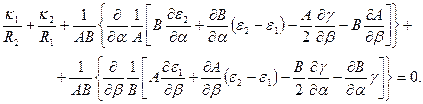
При выполнении расчётов оболочек пользуются линейным (5.41), а не гиперболическим (5.37) законом изменения деформаций сдвига элемента по толщине оболочки, поскольку, как и в теории расчёта кривых стержней, при малых отношениях 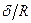различие в законах незначительно. Это справедливо и в отношении деформаций растяжения (сжатия).

5.8 Правила дифференцирования единичных ортов

При выводе формул настоящего раздела были использованы правила дифференцирования единичных ортов. Ниже дано обоснование этих правил. Как известно, в любой точке срединной поверхности оболочки можно показать тройку ортогональных единичных векторов 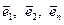, два из которых - 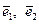направлены по касательным к координатным линиям 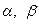, а третий 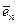- по нормали к поверхности (см. рис. 5.7,б). Вместе они образуют вектор .

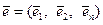Производные единичных векторов, составляющие вектор

,

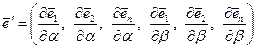как и сами векторы 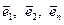, также являются векторными величинами. На этом основании они могут быть разложены по ортам триэдра 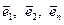. Такое разложение можно представить в матричном виде

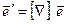. (5. 45)

с использованием дифференциального оператора в форме матрицы

,

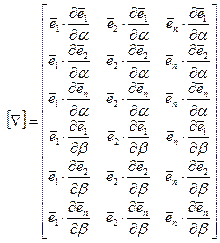если любой элемент данной матрицы считать проекцией, определяемой скалярным произведением.

Задача заключается в выводе формул, связывающих производные ортов с параметрами Ламэ и кривизнами поверхности оболочки. С этой целью следует вспомнить определение орт как производных векторной функции скалярного аргумента:

.

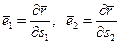В соответствии с правилом дифференцирования сложной функции 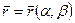можно написать:

,

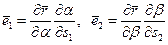где, как известно, 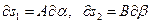. Воспользовавшись последними равенствами, находят:

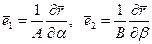. (5.46)

Вектор нормали, очевидно, определяется векторным произведением

.

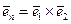Т. к. вектор производной 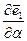ортогонален орту 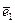, а 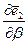- вектору 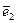, то в соответствии со скалярным произведением векторов

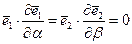. (5.47)

По той же причине справедливо и равенство

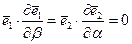. (5.48)

Несложное геометрическое построение (рис. 5.17) позволяет установить модуль вектора

.

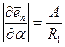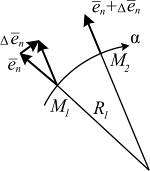
Рис. 5.17

А поскольку векторы 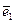и 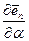коллинеарны, то

.

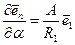Следовательно,

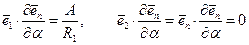. (5.49)

Аналогично выводятся и равенства:

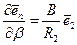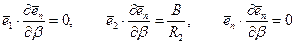, . (5.50)

Производные 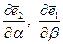находятся из условия

.

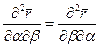Действительно, если принять во внимание определение векторов по (5.46), то это равенство принимает вид

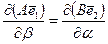. (5.51)

На основе полученного равенства путём раскрытия производных в одной части с сохранением другой приходят к двум соотношениям:

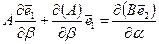, (5.52)

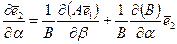. (5.53)

Из первого легко найти

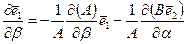, (5.54)

а из второго –

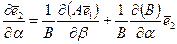. (5.55)

Без труда находится произведение

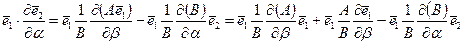. (5.56)

Последнее слагаемое в этом выражении равно нулю, поскольку орты 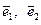ортогональны; по той же причине равно нулю и второе слагаемое, но теперь речь идёт о векторах .

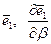Скалярное произведение 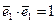, поэтому согласно (5.56)

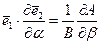. (5.57)

Аналогично устанавливается

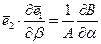. (5.58)

В силу ортогональности векторов 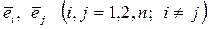справедливы равенства

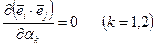
или

.

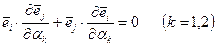Отсюда следует, что

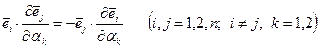. (5.59)

Используя равенство (5.59) в сочетании с (5.49), (5.50), (5.58), (5.59), можно получить последние шесть из восемнадцати проекций, входящих в матрицу . В итоге становится известной вся структура оператора дифференцирования , а именно:

.

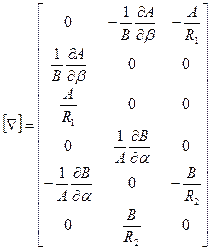* В геометрии поверхностей правая часть данного выражения называется первой квадратичной формой поверхности, а величины 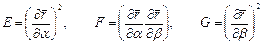- коэффициентами первой квадратичной формы.

* Правила дифференцирования ортов изложены в п. 5.8.

* Поверхность называется регулярной, если в каждой её точке можно провести касательную плоскость.

* В этой и других формулах параграфа значок дуги « 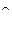» над каким-либо символом указывает на принадлежность вектора или иного параметра к деформированному состоянию оболочки.

** См. матрицу (5.60) в подразделе 5.8.

* Данные слои или поверхности оболочки называются эквидистантными. Всем параметрам, относящимся к этому слою, приписывается верхний индекс .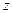

[1] На рис. 5.13 крышки над символами 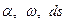относятся к параметрам деформаций слоя оболочки, отстоящего от срединной поверхности на расстоянии z.