Несимметричная нагрузка

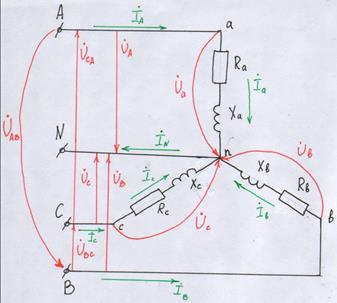
Обозначим на этой схеме линейные и фазные напряжения.

Кроме параметров схемы задано направление сети – линейное U_Л

1. Определим фазные напряжения. Если сопротивление фазы нагрузки подключено к генератору 4-мя проводами: линейными и нейтральным, то генератор принудительно задаёт на нагрузку свои симметричные фазные напряжения. U_A=U_B=U_C=U_Фе^jφ

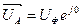
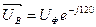
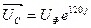
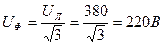
1. Для каждой фазы нагрузки строим треугольник сопротивлений и определяем полное сопротивление фазы и угол сдвига между напряжением и током.

Для А:

X_a Z_a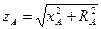

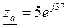
R_a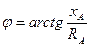

Для В: R_B=z_B z_B=R_B=10 φ_B=0, тогда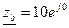

Для С:

Z_C -X_C φ_c= -90, тогда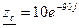

1. По закону Ома для каждой фазы находим фазные токи.

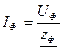
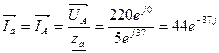
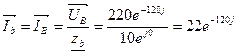
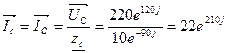
1. Определим линейные токи по формуле I_Ф=I_Л: I_a=I_A, I_b=I_B, I_c=I_C
2. Определим активную и реактивную мощность в каждой фазе. P_Ф=I_Ф²R_Ф
3. Определим активную и реактивную мощности всей трехфазной нагрузки:

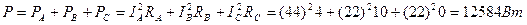
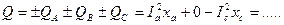
Где + - означает индуктивную нагрузку

- - означает ёмкостную нагрузку

7. Определяем ток нейтрального провода по первому закону Кирхгофа. 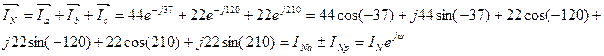8. Построим векторную диаграмму на комплексной плоскости и суммируем векторы.

Выводы:

1. Итак, соединение нагрузки звездой с нейтральным проводом всегда гарантирует равные фазные напряжения, не зависимо от сопротивлений фаз.

2. Для несимметричной нагрузки ток нейтрального провода не равен нулю а значит нейтральный провод необходим.

II. Соединение трёхфазной нагрузки звездой без нейтрального провода (симметричная нагрузка).

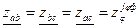
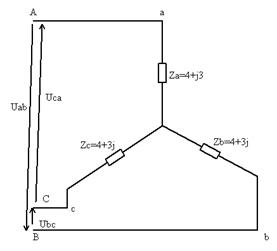
1. В данной схеме генератор задаёт на нагрузку только симметричную систему линейных напряжений U_AB и U_BC.

Так как нагрузка симметричная, то приложенные линейные напряжения распределяются поровну между прилегающими фазами. В результате Ua=U_b=U_c= 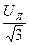а значит, что звезда без нейтрального провода пригодна для включения симметричной нагрузки.

Последовательность расчета смотрите для симметричной нагрузки, включённой по схеме «звезда с нейтральным проводом».

Соединение трёхфазной нагрузки звездой без нейтрального провода (несимметричная нагрузка).

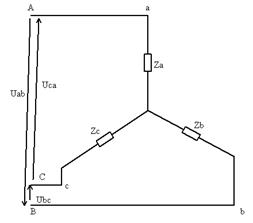
При несимметричной нагрузки, включённой по схеме «звезда без нейтрального провода», линейные напряжения генератора распределяются между прилегающими фазами, пропорционально их сопротивлениям, то есть на большем сопротивлении большее фазное напряжение, а на меньшем меньшее.

Требование обеспечения схемой равных фазных напряжений нарушается. Вывод: несимметричную нагрузку нельзя включать по схеме «звезда без нейтрального провода»

III. Симметричная нагрузка, включённая по схеме «треугольник»

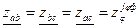
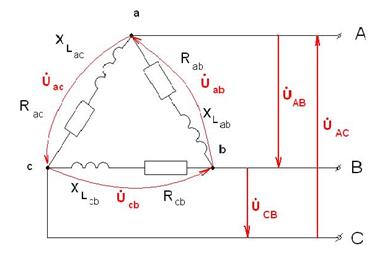
Для схемы треугольник U_Л=U_Ф U_AB=U_ab, U_BC=U_bc, U_AC=U_ac

1. Определим фазные напряжения.
2. Найдём фазные сопротивления, построив треугольник фазных сопротивлений.

X_Ф Z_Ф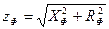

R_Ф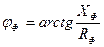

1. Определим фазные токи по закону Ома
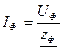
2. Определим активную и реактивную мощность всей трёхфазной нагрузки.

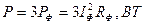
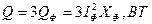
1. Линейные токи определяем графически по векторной диаграмме по первому закону Кирхгофа.

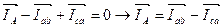остальные аналогично.

1. Строим равнолучевую звезду фазных и линейных напряжений.

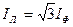
Вывод: схема треугольник гарантирует равные фазные напряжения при любой нагрузке и симметричной и несимметричной. Только для симметричной нагрузки 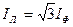а для несимметричной нагрузки определяется уравнениями первого закона Кирхгофа для точек a, b, c.