КРУГОВЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ

Цилиндрические оболочки применяются в различных областях строительства и машиностроения (покрытия промышленных предприятий, вокзалов, рынков, полые сваи фундаментов, трубы газопроводов, резервуары для воды, нефти и других жидкостей, корпуса ракет, тоннели метро и пр.). В разрезе они могут иметь круговое, эллиптическое и иное очертание (рис. 8.1).

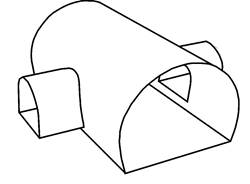
Рис. 8.1

8.1. Уравнения напряжённо - деформированного состояния цилиндрических оболочек

Срединная поверхность цилиндрической оболочки формируется путём вращения образующей (прямой) вокруг оси (рис. 8.2).

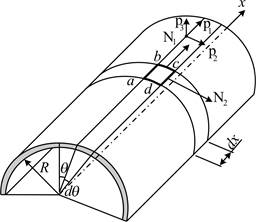
Рис. 8.2

Параметры Ламе для круговой цилиндрической оболочки находят по формулам (5.13):

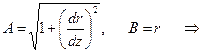
. (8.1)

Очевидно, главными радиусами кривизн срединной поверхности являются величины , где - радиус оболочки.

Уравнения равновесия оболочки могут быть выведены из общих условий равновесия оболочек (6.4), полученных в разделе 6 учебного пособия, если принять в них значения параметров Ламе по формуле (8.1). В цилиндрической системе координат уравнения записываются в следующем виде:

,

,

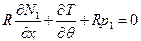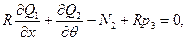(8.2,а)

,

.

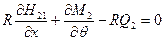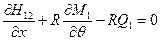На рис. 8.3 показан элемент оболочки, находящийся в равновесии под действием внутренних усилий, присутствующих в данных уравнениях.

Рис. 8.3

Система пяти уравнений легко сводится к эквивалентной системе трёх уравнений, для чего достаточно из четвёртого и пятого условий выразить величины поперечных усилий:

,

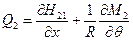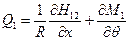
и подставить их во второе и третье условия (8.2,а). В итоге преобразований приходят к более обозримой системе:

,

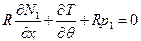, (8.2,б)

.

Деформации элемента срединной поверхности можно установить на основе общих геометрических зависимостей, выведенных в п. 5.7 лекции № 5:

,

,

,

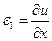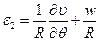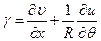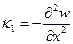, (8.3)

,

,

,

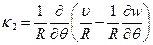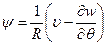где 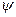- угол поворота касательной к поперечному сечению оболочки при деформации; формула для 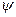получена на основе второй формулы (5.25), приведенной в лекции № 5.

Физические соотношения могут быть получены из общих формул (6.10) лекции № 6 в результате подстановки выражений указанных выше деформаций:

,

,

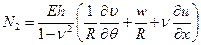, (8.4)

,

.

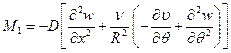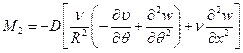Если воспользоваться данными выражениями и подставить их в условия равновесия (8.2,б), то последние могут быть представлены в перемещениях:

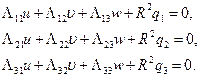(8.5)

Здесь ; ; ;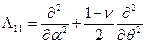

, ,

,

, ,

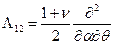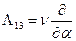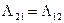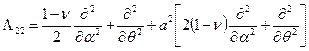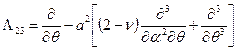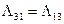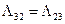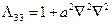
- дифференциальные операторы, в которых постоянные величины 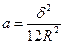и 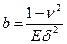характеризуют геометрические и физические параметры оболочки; 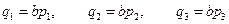- параметры внешней нагрузки.

Интегрирование полученной системы трёх дифференциальных уравнений (8.5) при некоторых допущениях возможно выполнить в аналитической форме. В п. 10.2 лекции № 10 рассматривается расчёт оболочек по т. н. полумоментной теории В. З. Власова, в которой пренебрегают влиянием изгибающих моментов в направлении оси х. В лекции № 11 выводится разрешающее уравнение общей (моментной) теории цилиндрических оболочек, в котором учитывается взаимовлияние всех без исключения внутренних силовых факторов. Небольшие упрощения, обусловленные структурой уравнения, позволяют найти решения ряда практических задач по расчёту коротких оболочек в аналитическом виде.

При действии симметричных нагрузок также возможно найти аналитическое решение системы уравнений, которые сводятся к одному, но более высокого порядка (см. п. 8.2).

8.2 Осесимметричное нагружение оболочки

Примером данного нагружения является гидростатическое действие жидкости на стенки вертикального резервуара (рис. 8.4,а).

а б

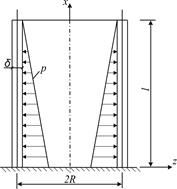
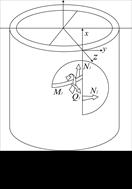
Рис. 8.4

Вследствие симметрии внешней нагрузки все усилия будут постоянны по окружности; при этом сдвигающие силы 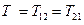и поперечная сила , а также крутящие моменты Н будут равны нулю. Оставшиеся усилия, показанные на рис. 8.4,б, в сочетании с нагрузкой 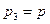образуют равновесную систему:

(8.2,в)

Она получена из условий равновесия элемента оболочки в виде сумм проекций на оси 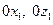и условия в виде .

Остальные уравнения равновесия удовлетворяются тождественно.

Выполнив дифференцирование последнего условия системы (8.2,в) и приняв во внимание предыдущее, легко установить, что

.

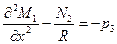С учётом физических соотношений

,

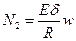, (8.6)

вытекающих их общих зависимостей (8.4) для цилиндрической оболочки, после небольших преобразований можно вывести уравнение деформированного состояния оболочки при осесимметричном нагружении в виде

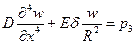. (8.7)

8.3 НДС вертикальной цилиндрической оболочки при гидростатическом нагружении

Решение линейного неоднородного дифференциального уравнения четвёртого порядка (8.7) при действии осесимметричной гидростатической нагрузки, которая распределена по линейному закону

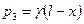(8.8)

может быть осуществлено различными методами, в том числе и численными.

В этом параграфе рассматривается аналитический способ интегрирования данного уравнения. В лекции № 9 приводится процедура численного решения рассматриваемой задачи с помощью ПЭВМ.

Следует заметить, что уравнение вида (8.7) встречается в сопротивлении материалов при изучении поведения балок на упругом основании. Аналитическое решение неоднородного дифференциального уравнения состоит из двух частей:

А) интеграла 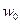однородного дифференциального уравнения вида

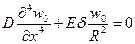, (8.9)

которое для удобства интегрирования приводится к стандартному виду

,

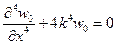где

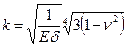
- физико - геометрический параметр оболочки.

Решение однородного уравнения ищется в виде

.

В соответствии с ходом интегрирования составляется характеристическое уравнение

.

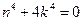Корни этого уравнения равны:

.

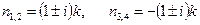Этим корням отвечают следующие линейно независимые функции:

,

являющиеся решениями однородного являющиеся решениями однородного уравнения уравнения. Их совокупность, может быть представлена как одна функция

, (8.10)

удовлетворяющая уравнению и содержащая к тому же произвольные постоянные 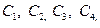. График данной функции, представлен двумя парами асимптотически убывающих кривых, показанных на рис. 8.5. Скорость приближения к нулю может быть оценена с помощью отношения амплитуд

,

взятых через отрезок, равный полуволне синусоиды 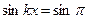, т.е. через 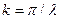. Следовательно, функция состоит из двух частей: первой с коэффициентом 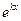, быстро убывающей по мере удаления от края 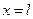и второй, убывающей от противоположного конца с коэффициентом .

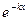Рис. 8.5

На этом основании при постановке граничных условий достаточно длинной оболочки можно ограничиться составлением двух независимых уравнений для определения двух постоянных 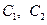, вместо системы четырёх – в общем случае, когда влиянием краёв друг на друга пренебречь нельзя (см. ниже примеры расчёта).

Б) вторая половина решения, соответствующая правой части уравнения (8.7) при 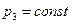, имеет вид 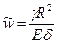. Убедиться в этом не представляет труда. Даже когда нагрузка меняется линейно - 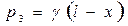, как в рассматриваемом случае гидростатического давления, легко убедиться, что решение ненамного сложнее, а именно,

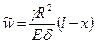. (8.11)

Прочем, частное решение может быть представлено в общем случае полиномом степени не выше третьей.

Таким образом, общий интеграл неоднородного дифференциального уравнения (7.7) имеет вид

.

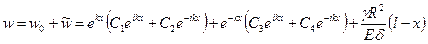Изгибающие моменты в соответствии с полученным решением равны

. (8.12,а)

На этом основании поперечные силы находятся по формуле

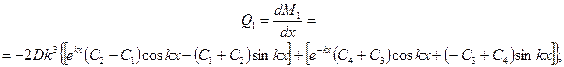продольные усилия в окружном направлении согласно

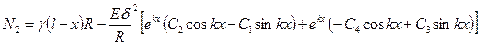. (8.12,б)

Произвольные постоянные 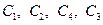находят их четырёх граничных условий, причём на каждом крае цилиндра ставят по два условия. В рассматриваемом случае постоянные 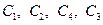определяются из следующих условий:

(8.13)

На основе данных условий с помощью выражений для перемещения (8.9) и усилий 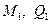можно составить четыре уравнения, из которых находятся постоянные интегрирования. В частности, из краевого условия

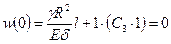
легко найти 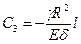, а условие

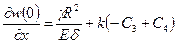
приводит к постоянной

.

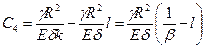Аналогично, два оставшихся условия позволяют установить .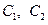

В итоге оказывается, что прогибы оболочки изменяются по высоте резервуара по закону

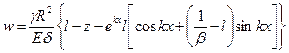. (8.14)

На основании данного решения изгибающие моменты и продольные усилия в окружном направлении следует вычислять по формулам:

, (8.15)

. (8.16)

Всплеск величины изгибающего момента вблизи опоры характеризует т. н. краевой эффект, возникающий в оболочках при наличии заделки в основании.

8.4 Анализ напряжений в оболочке при гидростатическом нагружении

Распределение внутренних усилий в оболочке находят по формулам (8.15) - (8.16). Наибольшие значения нормальных напряжений в продольном и окружном направлениях:

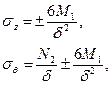(8.17)

возникают на внутренней и наружной поверхностях оболочки. В свою очередь, максимальная величина изгибающего момента в сечении стенки резервуара вблизи днища равна

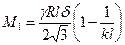, (8.18,а)

а растягивающего усилия -

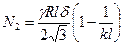. (8.18,б)

Графики распределения усилий 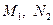по высоте оболочки, геометрические размеры которой указаны на рис. 8.6, получены при следующих механических характеристиках материала оболочки (железобетона): 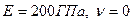.* Объёмный вес воды в резервуаре .

.

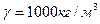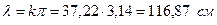Пунктиром на рисунке показан график изменения усилия 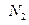в случае отсутствия защемления оболочки в основании. При этом моменты 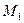вообще не возникают. Отсюда следует вывод о том, что в заделке у опоры давление воды воспринимается за счёт появления моментов и поперечных сил.

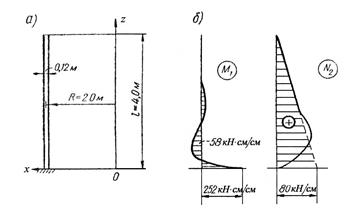
Рис. 8.6

Для коротких резервуаров, когда их высота соизмерима с длиной полуволны 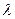, влиянием краёв друг на друга пренебрегать нельзя. Тогда постоянные находят из четырёх уравнений.

В лекции № 9, посвящённой численному методу анализа НДС оболочки,

дополнительно дана оценка влияния изменения по высоте толщины оболочки на прогибы и усилия при различных внешних нагрузках.

8.5 Примеры расчёта цилиндрических оболочек

Пример 1. Расчёт цилиндрической части корпуса батискафа

при всестороннем равномерном внешнем давлении

В рассматриваемом случае внешнего всестороннего давления на цилиндрическую оболочку корпуса батискафа, включая и крышки на торцах, вследствие круговой симметрии тела оболочки и приложенной нагрузки относительно оси цилиндра (рис. 8.7) напряжённо – деформированное состояние оболочки, как и при действии гидростатического давления, характеризуется отсутствием поперечных сил и крутящих моментов в окружном направлении.

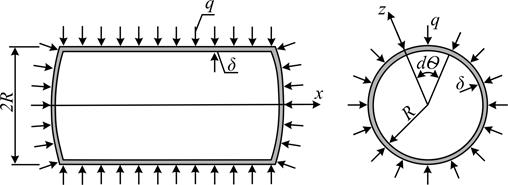
Рис. 8.7

Поскольку внешнее давление q нормально к срединной поверхности оболочки, то и сдвигающие усилия равны нулю. Таким образом, Очевидно, что продольные силы 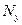и изгибающие моменты 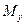в окружном направлении постоянны (рис. 8.8).

Для остальных внутренних усилий должны быть сохранены условия равновесия (8.2,a), т. е.

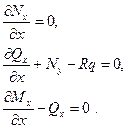(8.2,г)

В данной записи прежние цифровые индексы в обозначениях усилий заменены на буквенные и в дальнейшем приняты следующие обозначения:

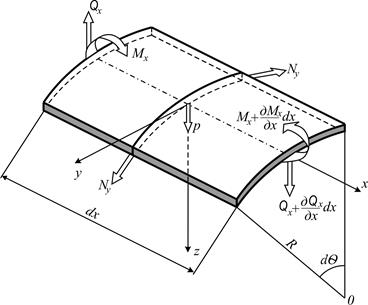
Рис. 8.8

Очевидно, что и продольные силы 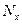также постоянны. Это вытекает из первого из приведенных условий. Кроме того, из третьего условия следует, что поперечные силы 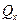и изгибающие моменты 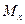в направлении образующей цилиндра связаны между собой той же дифференциальной зависимостью, что и аналогичные усилия в технической теории расчёта балок.

НДС рассматриваемой цилиндрической оболочки корпуса батискафа также можно описать одним дифференциальным уравнением четвёртого порядка, если систему (8.2,г), как и прежде, представить в перемещениях (через прогибы 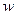оболочки); при этом уравнение усложняется по сравнению с (8.7).

Для вывода уравнения состояния, в первую очередь, необходимо определить величину силы 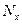в продольном направлении. Она постоянна и легко находится из условия равновесия одной из частей оболочки в виде на ось цилиндра

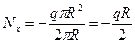. (8.19)

Знак «минус» здесь соответствует деформациям сжатия.

Воспользовавшись физическими уравнениями теории оболочек для нормальных усилий:

,

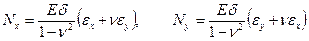и знанием модуля величины 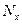согласно (8.19), легко установить связь между деформациями оболочки в основных направлениях.

Очевидно, из определения усилия 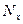нетрудно вывести формулу для деформаций оболочки в направлении образующей

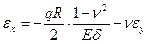. (8.20)

Деформацию оболочки в окружном направлении вследствие симметрии деформирования можно выразить через прогибы

. (8.21)

Учитывая это, теперь и величина нормальной силы в окружном направлении также может быть выражена через прогибы

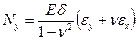= . (8.22)

Два последних условия равновесия системы (8.5), как известно, сводятся к одному к дифференциальному уравнению

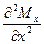
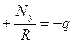. (8.23)

Если выразить изгибающие моменты 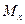через прогибы, то на основе данного уравнения с привлечением (8.22) можно вывести уравнение равновесия оболочки в перемещениях.

В общем случае в соответствии с физическими уравнениями теории оболочек моменты находятся по формулам:

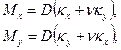(8.24)

где 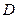- цилиндрическая жёсткость оболочки. Очевидно, при симметричном нагружении кривизна 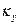оболочки в окружном направлении равняется нулю, поскольку прогибы в произвольном сечении х = с одинаковы

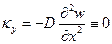. (8.25)

С учётом этого*

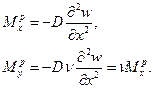(8.26)

Полная величина изгибающего момента 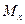при наличии нормальных сил 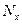в сечении оболочки находится по формуле

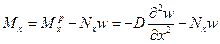. (8.27)

Дважды продифференцировав это выражение и подставив результат в (8.6), после группировки слагаемых, выводят разрешающее уравнение цилиндрической оболочки в перемещениях

. (8.28)

Полученное уравнение можно рассматривать как обобщение уравнения (8.7).

Интегрирование уравнения (8.28) можно выполнить различными способами, в том числе и численно, заменив непрерывные производные соответствующими дискретными выражениями, известными из работ автора по строительной механике [5]. Трудоёмкость решения существенно снижается, если пренебрегают влиянием нормальных усилий 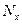, т. е. опускают в уравнении второе слагаемое

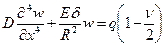. (8.29,а)

Поделив на и введя обозначение для множителя во втором слагаемом , уравнение записывают в виде, удобном для последующего интегрирования

. (8.29,б)

Сравнительные расчёты оболочек согласно (8.28) и (8.29,б) показывают, что влияние 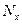на НДС оболочки действительно невелико**.

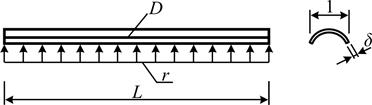
Замечание. Уравнение (8.29,б), как и уравнение (8.7), по форме ничем не отличается от уравнения балки постоянного сечения на упругом основании [4]). Несложно установить параметры модели (мнимой) «балки», соответствующие исходным физико-механическим характеристикам цилиндрической оболочки. Для этого необходимо выделить из оболочки двумя сечениями вдоль образующей полоску с расчётной шириной, равной единице, в окружном направлении; длина полоски определяется длиной самой оболочки (рис. 8.8,а).

Реакция основания «балки», заключённая в параметре

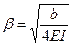
приведенного однородного уравнения балки

равна 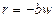( 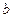- коэффициент постели основания балки).

Из условия равновесия полоски единичной ширины ( 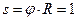) на ось 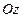вытекает (рис. 8.9,б), что

(*)

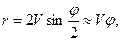где 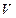- сжимающая сила, равная ( - толщина оболочки).

а

б

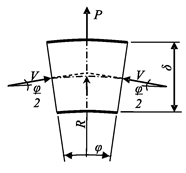
Рис. 8.9

С учётом данного определения V из равенства (*) вытекает, что

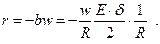
Отсюда находят некий «коэффициент постели оболочки»

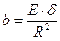
и соответствующий ему параметр - коэффициент затухания перемещений оболочки

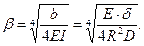
Очевидно, что при расчёте оболочки согласно (8.12) должна быть выполнена замена жесткости балки на изгиб 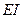на цилиндрическую жесткость оболочки .

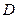Таким образом, для интегрирования уравнения оболочки могут быть использованы известные методики аналитического и численного расчёта балок на упругом основании [9]).

Пример 2. Расчёт на опоясывающую нагрузку

Указанная нагрузка представляет собой постоянное сосредоточенное силовое воздействие Р, распределённое по внешнему контуру в сечении х = с и приложенное по нормали к поверхности оболочки (рис. 8.10).

Рис. 8.10

Очевидно, при таком воздействии деформации оболочки будут симметричными и локальными.

Начало системы координат совмещается с любой точкой оболочки, взятой на поверхности в месте приложения силы в сечении х = 0. Положительное направление оси 0х может быть принято в любую сторону; ось 0z направляют перпендикулярно к оси цилиндра, а направление оси 0у принимают так, чтобы образовать правую систему координат.

Граничными условиями рассматриваемой задачи при решении уравнения (8.28) оболочки служат:

1. при , т. к. касательная в этом сечении не имеет наклона,

2. и 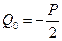, поскольку поперечная сила в сечении, очевидно, терпит разрыв на величину Р ( – погонная поперечная сила).

Положительные направления усили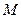й и 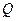сохраняются прежними (рис. 8.11).

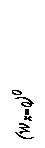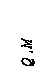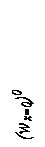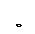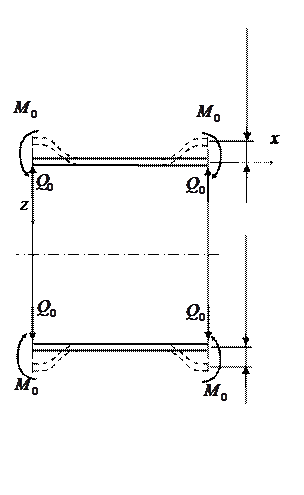Рис. 8.11

Воспользовавшись первым граничным условием, с помощью формулы

(**)

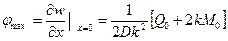легко найти связь между моментами и поперечными силами, приложенными в сечении х=0

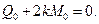
С учётом второго граничного условия величина момента равна:

. (8.30)

Выражение (**) для угла наклона нормали является вторым интегралом уравнения (8.12). Угол наклона находится путём решения вспомогательной задачи по анализу НДС длинной оболочки, подвергнутой действию усилий 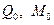, приложенных к её торцу (рис. 8.12).

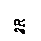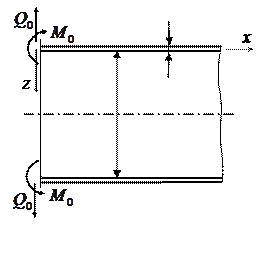Рис. 8.12

Несложно проверить выражение (**), выполнив интегрирование однородного дифференциального уравнения (8.12)

,

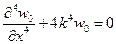где

- физико - геометрический параметр оболочки. Первый интеграл уравнения имеет вид (см. раздел 8 или [4]):

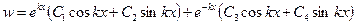. (8.31)

Для определения постоянных следует использовать следующие граничные условия:

1. На значительном удалении от торца оболочки, где приложены усилия 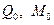, её прогибы столь малы, что при 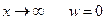. Это означает, что 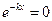при . Поэтому в решении остаётся только второе слагаемое

, (8.32)

2. Естественно, при и 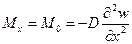. Эти условия используются для определения постоянных .

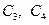После вычисления производных

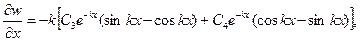(8.33,а)

(8.33,б)

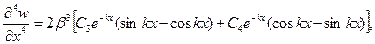(8.33,в)

легко определить постоянные 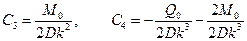. Подставив их в решение (8.32), находят прогибы оболочки

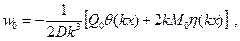(8.34)

где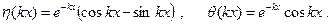

Теперь можно найти в явном виде как распределение усилий по длине оболочки

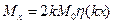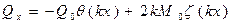, , (8.35)

где 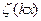= 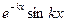, так и прогибов

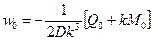. (8.36)

Максимальная величина прогиба в месте приложения силы составляет

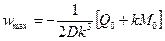, (8.37,а)

а угла наклона нормали к поверхности -

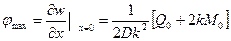. (8.37,б)

Таким образом, формула (**) достоверна.

Возвращаясь к решению основной задачи, теперь на основе формулы (8.31) можно установить распределение прогибов вдоль оси оболочки в зависимости от силы Р , приняв во внимание (8.30)

.

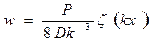Характер графика изменения прогибов оболочки по мере удаления от места приложения опоясывающей нагрузки показан на рис 8.13.

Рис. 8.13

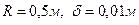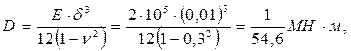
Из него видно, что перемещения оболочки очень быстро «затухают»; в частности, для оболочки с размерами при значениях , 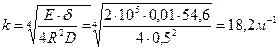на расстоянии 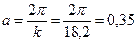м, составляющем около трети диаметра оболочки, их можно полагать нулевыми.

Очевидно, если длина оболочки 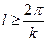, то нагрузка, приложенная на одном конце, не оказывает никакого влияния на другом; такие цилиндрические оболочки относятся к длинным.

Обладая данным решением, несложно установить усилия и прогибы оболочки, подверженной действию опоясывающей нагрузки, непрерывно распределённой вдоль образующей на конечном отрезке заданной длины.

Пример 3. Расчёт цилиндрических оболочек, усиленных шпангоутами

При расчёте оболочки, подкреплённой кольцами (шпангоутами) (рис. 8.14,а), используется те же формулы, что и при расчёте оболочки, нагруженной внутренним давлением.

а б

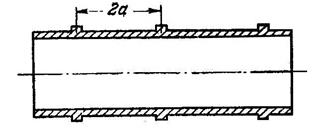
Рис. 8.14

Ключом, открывающим путь к решению рассматриваемой задачи, является условие совместности деформаций оболочки в сечении, где находится кольцо, в виде равенства прогибов, полученных ранее при расчётах оболочки на воздействие кольцевых моментов 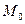и поперечных сил , в одном случае, и на внутреннее давление - в другом.

Условие совместности деформаций оболочки записывается в виде

,

если считать кольцо жёстким, или

,

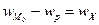когда кольцо деформируемо. Прогиб 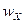обусловлен силой взаимодействия Х, возникающей между кольцом и оболочкой (рис. 8.15).

Рис. 8.15

Обращаясь к первому случаю, следует приравнять друг другу прогибы, определяемые формулой (8.36) и решением уравнения (8.29,б)

. (8.38)

Величина поперечной силы в месте сопряжения оболочки с кольцом равна

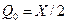. (8.39)

Значение изгибающего момента в том же сечении также можно выразить через силу взаимодействия Х, воспользовавшись условием отсутствия наклона касательной к поверхности оболочки в рассматриваемом сечении

.

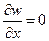Приравняв выражение углов наклона (8.37,б) нулю, т. е.

,

находят соотношение

.

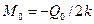С учётом определения (8.39) оно принимает вид . Подставив полученные значения 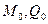в формулу (8.38)

находят величину силы взаимодействия

.

Из определения коэффициента затухания перемещений оболочки следует, что

,

и силу теперь можно выразить намного короче, а именно,

.

Тогда и погонная поперечная сила и изгибающий момент в месте сопряжения кольца с оболочкой записываются более компактно:

.

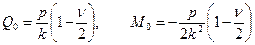Если кольцопри нагружении деформируется, то в условии совместности деформаций необходимо предварительно найти прогибы кольца, вызываемые силой Х. При их вычислении исходят из определения напряжений в кольце согласно

.

где А - площадь поперечного сечения кольца, 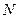- усилие в нём. Прогибы кольца равны

.

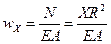В рассматриваемом случае условие совместности деформаций имеет вид

.

Отсюда следует, что

.

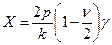Коэффициент характеризует уменьшение силы взаимодействия Х при наличии упругой податливости подкрепляющего кольца оболочки. При уменьшении толщины оболочки и увеличении площади сечения кольца, его величина приближается к единице.

Усилия в оболочке по мере удаления от кольца снижаются. Их распределение находят по формулам (8.35).

Пример. Найти изгибающие моменты в оболочке радиусом 30 см с толщиной стенки 1 см. Длина оболочки равна . Модуль упругости стали 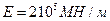, коэффициент Пуассона . Цилиндрическая жёсткость оболочки равна

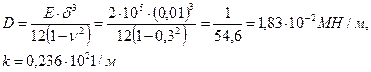
Граничное значение длины, при превышении которой оболочка относится к длинным находится по формуле (см. рис. 8.13)

.

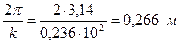Рассчитываемая оболочка относится к длинным, поскольку .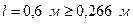

При наличии жёсткого кольца величина силы взаимодействия равна

.

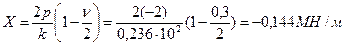Поперечная сила, соответствующая этой силе

= .

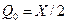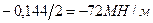Изгибающий момент в месте сопряжения кольца с оболочкой равен

.

Ординаты эпюры моментов по длине оболочки вычисляют по формуле (8.35)

.

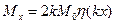Первая нулевая точка эпюры находится в сечении

.

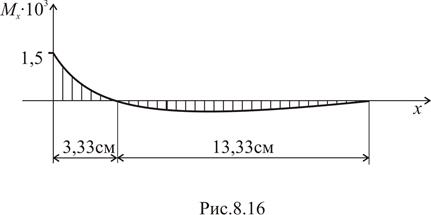
Вблизи второй нулевой точки на расстоянии 3,33+13,33=16,66 см. от кольца моменты практически исчезают.

8.6 Обзор теорий расчёта цилиндрических оболочек при других видах нагружения и закрепления кромок

Состояние цилиндрической оболочки, как видно из изложенного выше, зависит от её размеров, точнее, от отношения длины оболочки к диаметру. Очевидно, также, что состояние длинной трубы, по которой (медленно) течёт жидкость, при наличии опор на концах, подобно поведению балки на двух опорах. Конечно, в этих условиях расчёт оболочки по безмоментной теории будет заведомо противоречив. В длинной оболочке можно пренебречь величиной изгибающего момента 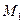в направлении образующей, и связанной с ним поперечной силой .

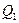Как же количественно находится граница, разделяющая цилиндрические оболочки по характеру напряжённо-деформированного состояния? Ответ на данный вопрос можно найти путём исследования НДС оболочек на основе общих уравнений теории оболочек путём введения предпосылок о значимости (или пренебрежении) тех или иных усилий на состояние оболочки в конкретных условиях работы. Сравнивая результаты теоретических расчётов при принятых гипотезах с экспериментальными данными можно строить методику расчётов оболочек с определёнными геометрическими параметрами и характером нагружения.

Как показали исследования, цилиндрические оболочки делятся на длинные, если отношение длины к радиусу 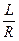больше 4. При относятся к средним, а при 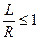- к коротким.

* В теории расчёта железобетонных оболочек при выводе общих соотношений коэффициент Пуассона 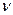обычно принимают равным нулю.

* Значок р над моментом М указывает на внешнее воздействие, которым оно вызвано.

** В лекции № 9 для решения данных уравнений использована эффективная процедура численного интегрирования.