Спонтанное и вынужденное излучение в квантовой системе

Чрезвычайно важный шаг по пути к созданию лазера был сделан А. Эйнштейном в 1916г. В своей работе "К квантовой теории излучения" Эйнштейн рассмотрел взаимодействие атомов с равновесным тепловым излучением с точки зрения гипотезы световых квантов. Он ввел понятия спонтанного и вынужденного излучений в квантовой системе и на этой основе нашел удивительно простой вывод формулы Планка.

Рассмотрим пару энергетических уровней атомов вещества, находящегося в равновесии с тепловым излучением при температуре Т.

Пусть нижний энергетический уровень имеет номер 1, верхний - номер 2. (рис.4). Обозначим число атомов, находящихся в состоянии с энергией e₁ через N₁, а число атомов с энергией e₂ через N₂. В состоянии теплового равновесия заселенности уровней N₁ и N₂ подчиняются распределению Больцмана:

N_i = const exp(e_i/kT). (1)

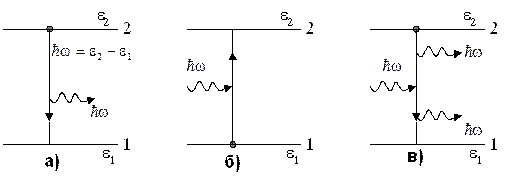
Рис.4. Схематическое представление трех процессов: а) спонтанное излучение;

б) поглощение; в) вынужденное излучение.

Данная пара уровней взаимодействует с излучением, частота которого подчиняется условию Бора:

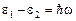. (2)

Следуя Эйнштейну, предположим, что возможны следующие типы радиационных процессов:

1. Спонтанное излучение (рис.4а). Квант света испускаемого при самопроизвольном переходе атома из состояния "2" в состояние "1". Вероятность этого процесса пропорциональна числу атомов на верхнем энергетическом уровне, поэтому можно записать

P₂₁^спонт=A₂₁N₂, (3)

где А₂₁ - коэффициент Эйнштейна.

2. Вынужденное поглощение (рис.4б). Атом поглощает квант света и переходит из состояния "1" в состояние "2". Вероятность этого процесса, индуцируемого излучением, пропорциональна спектральной плотности U(w, T) излучения на частоте w, а также числу атомов на нижнем энергетическом уровне. Следовательно, можно записать

P₁₂^вын=В₁₂N₁U(w, T), (4)

Коэффициент пропорциональности В₁₂ в этой формуле также называется коэффициентом Эйнштейна.

3. Вынужденное излучение (рис.4в). Переход атома из состояния "2" в состояние "1" происходит под действием резонансного кванта света и сопровождается излучением точно такого же кванта. Вероятность данного процесса есть

P₂₁^вын=B₂₁N₂U(w, Т), (5)

где В₂₁ - коэффициент Эйнштейна.

В состоянии равновесия переходы, сопровождающиеся испусканием и поглощением квантов света, должны, очевидно, уравновешивать друг друга. Это возможно, если вероятности перечисленных выше радиационных процессов удовлетворяют условию:

P₂₁^спонт + P₂₁^вын = P₁₂^вын. (6)

Подставив (3) - (5) в (6), получим уравнение

A₂₁N₂ + В₁₂N₁U(w, T) = B₂₁N₂U(w, Т). (7)

Принимая во внимание (1) и (2), из (7) находим следующее выражение для спектральной плотности равновесного теплового излучения:

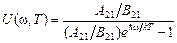. (8)

Отношения коэффициентов Эйнштейна можно найти из рассмотрения предельных случаев. В самом деле, пусть температура термостата стремится к бесконечности

Т → ∞. (9)

Тогда спектральная плотность теплового излучения будет не ограничено возрастать

U(w, T) → ∞, а населенности уровней будут выравниваться: N₁ → N₂.

В этих условиях из формулы (7) следует, что

В₁₂ = B₂₁. (10)

Теперь рассмотрим низкочастотный предел:

w → 0. (11)

В этом случае 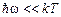, квантовая структура излучения не проявляется, и для спектральной плотности теплового излучения справедлива классическая формула Рэлея-Джинса

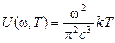. (12)

С другой стороны, при условии (11) из (10) следует, что

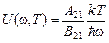. (13)

Сравнивая формулы (12) и (13), находим

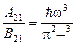. (14)

Наконец, подставив (10) и (14) в (8), получим

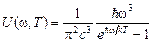. (15)

Итак, вывод формулы Планка завершен. Простота и ясность этого вывода убедительно свидетельствует в пользу гипотезы световых квантов, а также предположения Эйнштейна о существовании в квантовой системе трех типов радиационных процессов: спонтанного излучения, вынужденного поглощения и вынужденного излучения света. Весьма плодотворной сказалась также идея Эйнштейна вероятностного описания процессов испускания и поглощения световых квантов атомами.