Качество измерений и метрология

Качество измерений определяется их точностью. Точность измерений характеризуется их погрешностью. Абсолютной погрешностью измерений называют разность между найденным на опыте и истинным значением физической величины. Обозначая погрешность измерения величины х символом Dх, найдем

Dх = х_изм - х_ист . (14)

Относительная погрешность измерений равна отношению абсолютной погрешности к значению измеряемой величины:

d_х = (15)

Качество измерений обычно определяется именно относительной, а не абсолютной погрешностью. Одна и та же погрешность в 1 мм при измерении длины комнаты не играет роли, при измерении длины стола может уже быть существенна, а при определении диаметра болта совершенно недопустима. Это происходит потому, что относительная погрешность измерений в первом случае составляет » 2×10^-4, во втором »10^-3, а в третьем может составлять десятки процентов и более.

Вместо того, чтобы говорить об абсолютной и относительной погрешности измерений, часто говорят об их абсолютной и относительной ошибке. Здесь нет никакого различия. Однако цель измерений всегда состоит в том, чтобы узнать не известное заранее значение физической величины и найти если не ее истинное значение, то хотя бы значение, достаточно мало от него отличающееся. Поэтому формулы (14) и (15), определяющие величину погрешностей, для практики непригодны. При практических измерениях погрешности не вычисляются, а оцениваются. При оценках (которые редко удается провести с точностью лучше 20 - 30%) учитываются условия проведения эксперимента, точность методики, качество приборов и ряд других факторов.

Случайные и систематические погрешности измерений

Говоря о погрешностях измерений, следует, прежде всего, упомянуть о грубых погрешностях (промахах), возникающих вследствие недосмотра оператора или неисправности аппаратуры. Такие ошибки происходят, если, например, экспериментатор неправильно прочтет номер деления на шкале, если в электрической цепи произойдет замыкание и вследствие других подобных причин. Грубых ошибок следует избегать. Если установлено, что они произошли, соответствующие измерения нужно отбрасывать.

Не связанные с грубыми ошибками погрешности измерений бывают - случайные и систематические.

Погрешности измерений выявляют путем сравнения результатов, полученных при нескольких опытах, поставленных в одинаковых условиях. Два-три измерения следует производить всегда. Если результаты совпали, то на этом следует остановиться. Если же они расходятся, нужно попытаться понять причину расхождения. Часто она связана с тем, что прибор неисправен, ненадежно закреплен или плохо смазан, что электрические контакты не пропаяны или недостаточно зажаты. В этом случае, прежде всего, нужно попытаться исправить аппаратуру. Если устранить причину не удается, нужно произвести несколько измерений и записать все полученные результаты. Ниже будет рассказано о том, как следует поступать с полученными числами.

Многократно повторяя одни и те же измерения, можно заметить, что довольно часто их результаты не в точности равны друг другу, а «пляшут» вокруг некоторого среднего. Погрешности, меняющие величину и знак от опыта и опыту, называют случайными.

Случайные погрешности могут быть связаны с трением (из-за которого приборная стрелка вместо того чтобы останавливаться в правильном положении, «застревает» вблизи него), с люфтами в механических приспособлениях, с тряской, которую в городских условиях трудно исключить, с несовершенством объекта измерений (например, при измерении диаметра проволоки, которая из-за случайных причин, возникающих при изготовлении, имеет не вполне круглое сечение) или с физическими особенностями самой измеряемой величины.

Систематические погрешности сохраняют свою величину (и знак!) во время эксперимента. Они могут быть связаны с ошибками приборов (неправильная шкала, неравномерно растягивающаяся пружина, неравномерный шаг микрометрического винта, не равные плечи весов) и с самой постановкой опыта (определение скорости поезда по проходимому им расстоянию на участке, где движение происходит с небольшим ускорением, которое ускользнуло от внимания оператора, влияние трения и т. д.). В результате систематических погрешностей, разбросанные из-за случайных ошибок результаты опыта колеблются не вокруг истинного, а вокруг некоторого смещенного значения.

Рис. 1 поясняет различие между случайными и систематическими погрешностями. В ситуации, изображенной на рис. 1, а, систематическая погрешность пренебрежимо мала. Измеренные значения отличаются от истинного вследствие случайных ошибок опыта. На рис. 1, б изображены результаты опыта при наличии как случайных, так и систематических погрешностей.

Систематические погрешности опыта могут быть изучены и скомпенсированы, путем внесения поправок в результаты измерений. Неравноплечность весов можно учесть, меняя местами грузы на чашках весов. Неточность шкал электроизмерительных приборов можно установить, сравнивая их показания с показаниями более точных приборов, и т. д.

Различие между случайными и систематическими погрешностями не является абсолютным. Оно связано с постановкой измерительного эксперимента. Например, производя измерения тока несколькими разными амперметрами систематическую ошибку, связанную с неточностью шкалы, мы превращаем в случайную, величина (и знак!) которой зависит от того, какой поставлен амперметр в данном опыте и т.д. Однако, во всяком данном опыте - при заданной его постановке - различие между систематическими и случайными погрешностями всегда можно и нужно устанавливать с полной определенностью.

Случайные погрешности.

Случайные величины, к которым относятся случайные погрешности, изучаются в теории вероятностей и в математической статистике.

Рассмотрим для примера данные, полученные при измерениях массы тела на весах, у которых имеется область застоя из-за трения призмы на подушке. Пусть масса тела близка к 48 мг, результат измерений удается отсчитать по шкале с точностью до 0,1 мг. Имеем в миллиграммах: 48,0; 47,9; 47,5; 48,2; 48,4; 47,8; 48,6; 48,3; 47,8; 48,1; 48,2. Вместо одного нужного нам результата мы получили одиннадцать. Что делать с полученными цифрами? Как найти действительное значение массы тела и как оценить погрешность полученного результата? Этот вопрос подробно изучается в математической статистике. Рассмотрим соответствующие правила без вывода.

В качестве наилучшего значения для измеренной величины обычно принимают среднее арифметическое из всех полученных результатов:

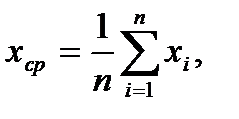(16)

в нашем случае получим

Этому результату следует приписать погрешность, определяемую формулой

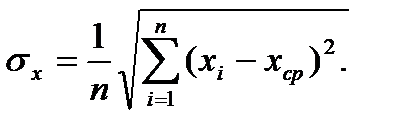(17)

В нашем случае

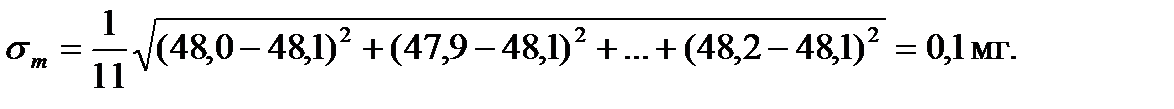
Результат опыта записывается в виде

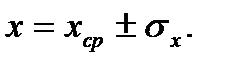(18)

В нашем случае m = (48,1 ± 0,1) мг.

Рассмотрим формулы (16) и (17). Прежде всего, попытаемся понять, как зависит результат расчета от числа измерений.

Формула (16) показывает, что х_ср слабо зависит от числа измерений. Все слагаемые, входящие в числитель, приблизительно равны друг другу. Их сумма пропорциональна числу слагаемых. После деления на знаменатель получается величина, мало зависящая от числа измерений, Так, конечно, и должно быть. Среднее измеренное значение - при правильной методике опыта - всегда лежит вблизи истинного значения и в разных независимых сериях измерений испытывает вокруг него небольшие случайные колебания.

Погрешность опыта, определяемая формулой (17), с увеличением числа измерений n уменьшается как Ön:

(19)

(Число членов суммы в (17) растет как n, числитель (17) поэтому увеличивается как Ön, а все выражение уменьшается как Ön.)

Этот результат является очень важным. По мере увеличения числа опытов ошибки в сторону преувеличения и преуменьшения результата все лучше компенсируют друг друга, и среднее значение приближается к истинному. В нашем примере одиночные отсчёты отличаются от среднего на несколько десятых, а погрешность результата, полученного при усреднении всех измерений, составляет всего одну десятую.

Корень из n определяет среднеквадратичную погрешность одного измерения. При обсуждении смысла величины s следует помнить, что истинную величину погрешности невозможно узнать до тех пор, пока из каких-либо других опытов (или соображений) не удастся определить искомую величину с существенно лучшей точностью.

Как уже отмечалось, погрешность результата не столько определяют, сколько оценивают. Оценка (17) подобрана так, что при проведении многочисленных серий измерений погрешность в 2/3 случаев оказывается меньше s_х, а в 1/3 случаев больше, чем s_х .

Иначе говоря, если провести не одну серию из 11 взвешиваний, а десять таких серий, то можно ожидать, что в шести или семи из них усредненный результат будет отличаться от истинной массы тела меньше чем на 0,1 мг, а в остальных случаях больше чем на 0,1 мг.

Погрешность, определенную с достоверностью 2/3, обычно называют стандартной (или среднеквадратичной) погрешностью измерений, а её квадрат - дисперсией. Можно показать, что, как правило, погрешность опыта только в 5% случаев превосходит ±2s и почти всегда оказывается меньше ±3s.

На первый взгляд из сказанного можно сделать вывод, что, беспредельно увеличивая число измерений, можно даже с самой примитивной аппаратурой получить очень хорошие результаты. Это, конечно, не так. С увеличением числа измерений уменьшается только случайная погрешность опытов. Методические погрешности и погрешности, связанные с несовершенством приборов (например, с неправильностью их шкалы), при увеличении числа опытов ведут себя скорее наоборот и в лучшем случае не меняются.

В приведенном выше примере результат взвешивания округлялся до десятых долей миллиграмма. Это делалось потому, что сотых долей отсчитать было нельзя. Ошибка отсчета составляла при этом около 0,1 мг. Поэтому погрешность результата, ни при каком числе опытов не может быть сделана меньше.

Число опытов в нашем случае было выбрано разумно. Из приведенных в таблице цифр ясно, что при однократном измерении можно ошибиться на несколько десятых. Среди цифр встречаются результаты, отличающиеся на 0,3 и даже на 0,5 от среднего. После усреднения по 11 измерениям погрешность существенно уменьшилась. Но если окажется нужным узнать массу тела с лучшей точностью, то недостаточно просто увеличить число измерений. Придется взять более точные весы, позволяющие производить измерения не до десятых, а, скажем, до сотых долей миллиграмма.

Необходимо заметить, что формула (17) позволяет хорошо оценивать величину стандартной погрешности только в тех случаях, когда число опытов оказывается не меньше 4 ¸ 5. При меньшем числе опытов лучше применять другие, более сложные оценки. Однако надежность всех этих оценок при малом числе измерений оказывается невысокой.

Систематические погрешности

Оценку систематических погрешностей экспериментатор производит, анализируя особенности методики, паспортную точность приборов и производя контрольные опыты.

Отметим различие в правилах определения погрешностей и в определении класса точности.

Погрешности принято характеризовать среднеквадратичными ошибками. При многочисленных измерениях реальная ошибка опытов только в 2/3 случаев меньше среднеквадратичной, а в 1/3 случаев превосходит её.

Класс точности определяет максимально возможное значение погрешности. Приборы, которые могут давать, хотя бы иногда, бо^¢льшие погрешности, должны быть отнесены к другому классу.

Такое различие в определениях неудобно. В научных публикациях принято приводить именно среднеквадратичную ошибку, а вовсе не максимальную. Строгих формул для перевода одних погрешностей в другие не существует, поэтому можно пользоваться следующим простым правилом: чтобы оценить среднеквадратичную погрешность измерений приборами, следует погрешность, определяемую классом точности прибора, разделить на два.

Как уже отмечалось, класс приборов определяет максимальную погрешность, величина которой не меняется при переходе от начала к концу шкалы. Относительная ошибка при этом резко меняется, поэтому приборы обеспечивают хорошую точность при отклонении на всю шкалу и не дают её при измерениях в начале шкалы. Отсюда следует рекомендация: выбирать прибор (или шкалу многошкального прибора) так, чтобы стрелка прибора при измерениях заходила за середину шкалы.

Говоря о систематических погрешностях измерений в механике, следует сказать несколько слов об ошибке отсчета «на глаз». Большинство приборов не имеет нониусных шкал. При этом доли деления отсчитываются на глаз. Эта ошибка составляет 1 - 2 десятых доли деления. При отсчётах следует следить за тем, чтобы луч зрения был перпендикулярен шкале. Для облегчения установки глаза на многих приборах устанавливается зеркало (зеркальные приборы). Глаз оператора установлен правильно, если стрелка прибора закрывает свое изображение в зеркале. При работе с электроизмерительными приборами отсчет должен включать число целых делений и число десятых долей деления, если отсчет может быть произведен с этой точностью (если стрелка или зайчик не ходят и не дрожат, что может сделать аккуратный отсчет невозможным).

Поясним указанное правило. Шалы электроизмерительных приборов обычно изготовляют так, что одно деление шкалы приблизительно равно максимальной погрешности прибора. Зачем же в этом случае отсчитывать десятые доли деления? Дело в том, что при измерениях, при расчетах и при записи результатов, кроме надежно известных значащих цифр, всегда указывается одна лишняя. Такая процедура, среди прочих, имеет и то преимущество, что позволяет вовремя замечать, мелкие нерегулярности и исследуемых зависимостей. Если, например, стрелка прибора при измерениях отклонилась на полделения назад, этот результат является надежным и в том случае, когда погрешность прибора равна целому делению.

Несколько слов о точности линеек. Металлические линейки очень точны: миллиметровые деления наносятся с погрешностью не более ± 0,05 мм, а сантиметровые - не хуже, чем с точностью 0,1 мм. Погрешность измерений, производимых с помощью таких линеек, практически равна погрешности отсчета на глаз. Деревянными или пластиковыми линейками лучше не пользоваться: их погрешности неизвестны и могут оказаться неожиданно большими. Исправный микрометр обеспечивает точность 0,01 мм, а погрешность измерений штангенциркулем определяется точностью, с которой может быть сделан отсчет, т. е. точностью нониуса (у штангенциркулей цена делений нониуса составляет обычно 0,1 или 0,05 мм).

Сложение случайных и систематических погрешностей

В реальных опытах присутствуют как систематические, так и случайные ошибки. Пусть они характеризуются стандартными погрешностями s_сист и s_случ . Суммарная погрешность находится по формуле

(20)

Поясним эту формулу. Систематическая и случайная ошибки могут, в зависимости от случая, складываться или вычитаться друг из друга. Как уже говорилось, точность опытов принято характеризовать не максимальной (и не минимальной), а среднеквадратичной погрешностью. Поэтому правильно рассчитанная погрешность должна быть меньше суммы s_случ + s_сист и больше их разности s_случ - s_сист . Легко видеть, что s_полн , определенная формулой (20), удовлетворяет этому условию. В самом деле, все величины s положительные. Поэтому

Знак равенства возникает только в том случае, когда одна из погрешностей равна нулю. Аналогично имеем

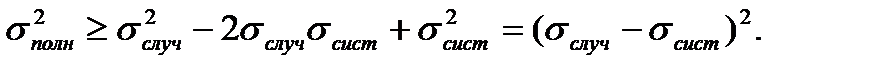
Формула (20) показывает, что при наличии как случайной, так и систематической погрешности полная ошибка опыта больше, чем каждая из них в отдельности, что также является вполне естественным.

Обратим внимание на ещё одну важную особенность формулы (20). Пусть одна из ошибок, например s_случ , в 2 раза меньше другой. Тогда

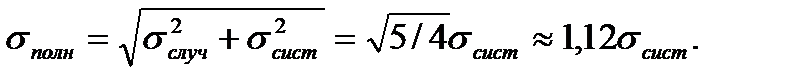
Как мы уже говорили, погрешности редко удается оценить с точностью лучше 20%. Но в нашем примере с точностью 20% s_полн = s_сист . Таким образом, меньшая погрешность почти ничего не добавляет к большей, даже если она составляет половину от нее.

Этот вывод очень важен. В том случае, если случайная ошибка опытов вдвое меньше систематической, нет смысла производить многократные измерения, так как полная погрешность опыта при этом практически не уменьшается. Измерения достаточно произвести 2 - 3 раза, чтобы убедиться, что случайная ошибка действительно мала.

Обработка результатов при косвенных измерениях

Если исследуемая величина равна сумме или разности двух измеренных величин,

А =В ± С, (21)

то наилучшее значение величины А равно сумме (или разности) наилучших значений слагаемых: А_наил = В_наил + С_наил , или, как рекомендовано выше,

(22)

Здесь и в дальнейшем угловые скобки (или черта сверху) означают усреднение: вместо того, чтобы писать А_ср, будем пользоваться обозначением <А> (или 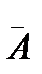), и т. д.

Среднеквадратичная погрешность s_А, если величины В и С независимы, находится по формуле

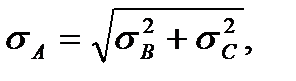(23)

т. е. погрешности, как всегда, складываются квадратично. (Иначе говоря, складываются не погрешности, а дисперсии результатов измерений.) При обсуждении формулы (23) следует использовать те же аргументы, которые были приведены в связи с формулой (20).

В том случае, если искомая величина равна произведению или частному двух других,

А = В×С или А = В/С, (24)

то

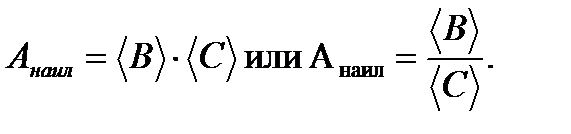(25)

Относительная среднеквадратичная погрешность произведения и частного независимых величин находится по формуле

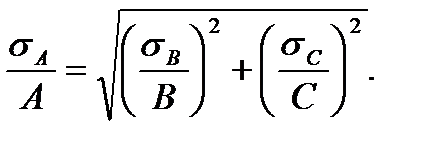(26)

Приведем расчетные формулы для случая, когда

А = В^b×C^g×E^e×...... (27)

Наилучшее значение А связано с наилучшими значениями В, С, Е и т. д. той же формулой (14), что и каждое конкретное значение. Относительная среднеквадратичная погрешность величины А при независимых В, С, Е... находится по формуле

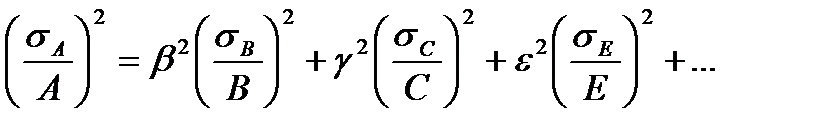(28)

Наконец, приведем для справок общую расчетную формулу. Пусть

А = f (В, С, Е, ...), (29)

где f - произвольная функция величин В, С, Е и т. д. Тогда

А_наил= f (В_наил , С_наил , Е_наил , ...) (30)

Формула (20) справедлива как в том случае, когда В_наил , С_наил , и т.д. непосредственно измерены, так и в том случае, если они найдены по измеренным значениям других величин. В первом случае значения В_наил , С_наил , и т.д., как уже указывалось, равны <В>, <С> и т. д. Погрешность А находится по формуле

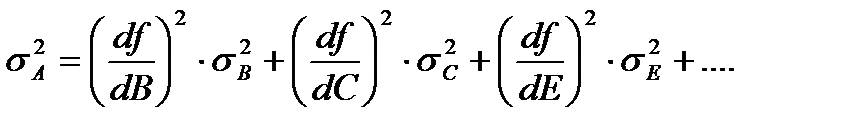(31)

Частные производные следует вычислять при наилучших значениях аргументов. Все приведенные в этом параграфе формулы являются частными случаями (30) и (31).

Рассмотрим некоторые следствия, которые могут быть получены из анализа формул, приведенных в этом разделе. Прежде всего, заметим, что следует избегать измерений, при которых искомая величина находится как разность двух больших чисел. Так, толщину стенки трубы не следует определять, вычитая ее внутренний диаметр из внешнего диаметра и конечно деля результат пополам. Относительная погрешность измерения, которая обычно представляет главный интерес, при этом сильно увеличивается, так как измеряемая величина - в нашем случае толщина стенки - мала, а ошибка в ее определении находится путем сложения погрешностей измерения обоих диаметров и поэтому возрастает.

Следует также помнить, что погрешность измерения, которая составляет, например, 0.5% от величины внешнего диаметра, может составить 5% и более от толщины стенки.

При измерениях, которые затем обрабатываются по формуле (24) (например, при определении плотности тела по его массе и объему), следует определять все измеряемые величины с приблизительно одинаковой относительной точностью. Так, если объем тела измерен с погрешностью 1%, то при взвешивании с погрешностью 0.5% его плотность определяется с точностью 1.1%, а при взвешивании с погрешностью 0.01% - с точностью 1%, т. е. с той же, практически, точностью. Тратить силы и время на измерение массы тела с точностью 0.01% в этом случае, очевидно, не имеет смысла.

При измерениях, которые обрабатываются по формуле (31), следует обращать главное внимание на точность измерения величины, входящей в расчетную формулу с наибольшим показателем степени.

Прежде чем приступать к измерениям, всегда нужно подумать о последующих расчетах и выписать формулы, по которым будут рассчитываться погрешности. Эти формулы позволят понять, какие измерения следует производить особенно тщательно, а на какие не нужно тратить больших усилий.

Запись результатов. Точность расчетов

Результат измерения записывается в виде, определяемом формулой (18). Запись m = 0.876 ± 0.008г означает, что в результате измерений для массы тела найдено значение 0.876г со стандартной погрешностью 0.008г. Подразумевается, что при вычислении стандартной погрешности учтены как случайные, так и систематические ошибки.

При записи погрешности следует округлять ее величину до двух значащих цифр, если первая из них является единицей, и до одной значащей цифры во всех остальных случаях. Так, правильно писать ±3; ±0.2; ±0.08; ±0.14 и не следует писать ±3.2; ±0.23; ±0.084. Не следует также округлять ±0.14 до ±0.1.

Поясним это правило. Уже говорилось, что погрешность эксперимента редко удается определить с точностью лучше 20%. Если вычисление стандартной ошибки приводит к 0.14, то округление 0.14 до 0.1 изменяет величину погрешности на целых 40%, в то время как округление до 0.3 числа 0.26 или 0.34 изменяет погрешность менее чем на 15%, т.е. несущественно.

При записи измеренного значения последней должна указываться цифра того десятичного разряда, который использован при указании погрешности. Один и тот же результат с указанием погрешности запишется в виде: 1.2 ± 0.2; 1.24 ± 0.03; 1.243 ± 0.012 и т.д. Последняя из, указанных, цифр или даже две из них, в этом примере, является сомнительной, а остальные достоверными.

Сформулированное правило следует применять и в тех случаях, когда некоторые из цифр являются нулями. Если при измерении получен результат m = 0.900 + 0.004г, то писать нули в конце числа 0.900 необходимо. Запись m = 0.9 означала бы, что о следующих значащих цифрах ничего не известно, в то время как измерения показали, что они равны нулю. Аналогичным образом, если масса тела равна 58.3кг (с погрешностью в десятых долях килограмма), то не следует писать, что она равна 58 300г, так как эта запись означала бы, что тело взвешено с точностью несколько граммов. Если результат взвешивания должен быть выражен в граммах, то в нашем случае нужно писать 5.83×10⁴ г.

Необходимая точность расчетов определяется тем, что расчет не должен вносить в измерения дополнительной погрешности. Обычно в промежуточных расчетах сохраняется один лишний знак, который в дальнейшем при записи окончательного результата будет отброшен.

Изображение экспериментальных результатов на графиках

Результаты экспериментов обычно представляют не только в виде таблиц, но и в графической форме. Для графиков следует использовать специальную бумагу (миллиметровую, логарифмическую или полулогарифмическую). При их отсутствии иногда приходится (хотя это крайне нежелательно!) пользоваться бумагой «в клеточку» или белой бумагой, на которой карандашом нанесена сетка. Не следует выбирать слишком малый или слишком большой лист бумаги. Удобна бумага размером в обычный тетрадный лист (или в развернутый лист). Полезно пользоваться листами миллиметровки из блокнотов (или планшетов) для диаграмм.

При построении графиков следует разумно выбирать масштабы, чтобы измеренные точки располагались на всей площади листа. Масштаб должен быть удобным. Клеточка графика (или миллиметр миллиметровой бумаги) может соответствовать 0,1; 0,2; 0,5; 1; 2; 5; 10 и т. д. единицам измеряемой величины, но не 2,5; 3; 4; 7 и т. д. При неудобном масштабе нанесение экспериментальных точек на график и использование графика требуют неоправданно большого времени и нередко сопровождаются досадными ошибками.

Графическое представление результатов позволяет быстро понять характерные черты наблюдаемой зависимости и обнаружить ошибочные результаты. При рассмотрении графика можно увидеть, что какая либо точка выпадает из закономерности. Это может означать, что при ее измерении была допущена ошибка. Если это не так, то в районе этой точки искомая зависимость имеет резко выраженную особенность. Именно такие особенности и представляют наибольший интерес для экспериментатора. Поэтому нужно внимательно промерить область, расположенную вблизи выпавшей точки, и постараться детально изучить форму кривой в районе найденной особенности.

Точки, наносимые на графики, должны изображаться четко и ясно. Их следует отмечать карандашом, так как иначе ошибочно нанесенную точку нельзя удалить с графика, не испортив его. Никаких линий и отметок, поясняющих построение точек, на график наносить нельзя, так как они загромождают рисунок и мешают анализировать результаты.

Точки, полученные в разных условиях (при нагревании и при охлаждении, при увеличении и при уменьшении нагрузки, в разные дни и т. д.), полезно наносить разными цветами или разными значками. Это помогает увидеть новые явления.

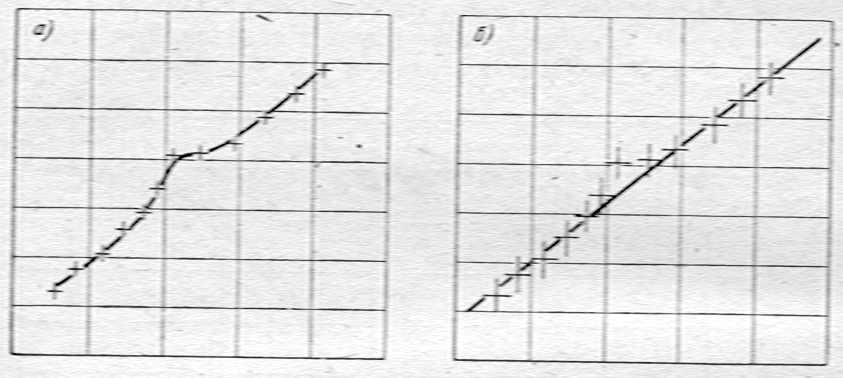
Способ изображения на графике экспериментальных результатов зависит от того, известна ли их случайная погрешность. Если случайная погрешность неизвестна (что чаще всего и бывает), то результаты изображаются точками, а если известна, то лучше изображать их не точками, а крестами. Полуразмер креста по горизонтали должен быть равен стандартной погрешности по оси абсцисс, а его вертикальный полуразмер - погрешности по оси ординат. В том случае, если одна из ошибок - из-за своей малости - не может быть изображена графически, результаты изображаются черточками, вытянутыми на величину ±s в том направлении, где погрешность не мала. Важность такого способа изображения результатов ясна из рисунков, на которых изображены одни и те же экспериментальные точки при разных погрешностях измерений.

График (а) несомненно, указывает на нерегулярный ход изучаемой зависимости. Эта зависимость изображена на рисунке кривой линией.

Те же данные при больших ошибках опыта (б) с успехом описываются прямой линией, так как только одно измерение отступает от этой кривой больше, чем на стандартную ошибку (и меньше, чем на две такие ошибки).

То обстоятельство, что при ошибках на (а) данные требуют проведения кривой, а на (б) этого не требуют, проясняется лишь при изображении экспериментальных результатов в виде креста погрешностей.

Из сказанного отнюдь не следует, что, изображая результаты опытов не крестами погрешностей, а простыми точками, мы всегда совершаем ошибку. Если величины погрешностей уже ясны при построении графика, следует, конечно, их изображать. Чаще всего, однако, эти погрешности к моменту построения графика неизвестны, и их разумно определять из разброса точек на графике. В этих случаях экспериментальные данные естественно изображать простыми точками.

Заметим также, что кривые на графиках не всегда проводятся через экспериментальные точки. Нередко кривые изображают зависимость, полученную не из эксперимента, а из теоретических соображений (или из других опытов). При построении таких кривых возникает необходимость предварительно нанести на график ряд расчетных точек. Эти точки должны наноситься еле заметным образом, чтобы их нельзя было спутать с четкими точками (или крестами), изображающими экспериментальные данные. Лучше всего, чтобы расчетные точки вообще не были заметны.

Оси графика должны иметь ясные, четкие обозначения. Рядом с делениями, на удобных расстояниях, должны быть нанесены цифры, позволяющие установить значения, соответствующие делениям шкалы. Цифры принято располагать по краям сетки. На графиках должно быть указано, какая физическая величина и в каком масштабе на ней отложена.

Проведение кривых через экспериментальные точки

Через экспериментальные точки всегда следует проводить самую простую кривую, совместимую с этими точками, т.е. кривую, от которой экспериментальные данные отступают, как правило (в 2/3 случаев), не более чем на стандартную ошибку. Примеры таких кривых и изображены на рисунке. Не следует придавать кривым никаких изгибов, если экспериментальным данным, в пределах ошибок, можно удовлетворить и без этого.

При проведении кривой нужно следить за тем, чтобы на каждом достаточно большом ее участке экспериментальные точки располагались как выше, так и ниже кривой. Так, на рис. а левая часть кривой изображена верно, а правая – неверно, т.к. ни одна из точек графика не лежит выше этой части кривой.

Математическое правило проведения кривых заключается в следующем. После того как тип кривой (прямая, окружность, парабола, и т.д.) из тех или иных соображений (чаще всего теоретических) выбран, параметры кривой должны быть подобраны так, чтобы сумма квадратов отклонения от нее всех экспериментальных точек была наименьшей (правило «наименьших квадратов»). Пользоваться этим правилом при графическом изображении экспериментальных зависимостей затруднительно, но при некотором опыте графические изображения данных измерений оказываются практически оптимальными.

При графической обработке результатов следует помнить, что на глаз точно провести через экспериментальные точки можно только прямую линию. Поэтому при построении графика следует стремиться к тому, чтобы ожидаемая зависимость имела вид прямой линии.

Так, исследуя закон падения тел, мы вправе ожидать, что результаты будут описываться законом S = gt²/2. Если откладывать по осям графика S и t, то точки лягут на параболу, которую провести на глаз почти невозможно. Но если откладывать по осям S и t², или S и gt²/2, то график приобретет вид прямой линии. Одно из этих представлений и должно быть выбрано для построения графика.

Производя измерения, всегда следует заботиться о том, чтобы точки на графике, который потом будет построен, располагались достаточно равномерно. В нашем примере, решив, например, строить график в переменных S и t², следует выбирать время измерений так, чтобы точки лежали на равных расстояниях в шкале t², а не t. Выбор равных интервалов времени (0,5; 1; 1,5; 2 с. и т.д.) приведет к тому, что в правой части графика точки будут лежать редко, а в левой части - слишком близко друг к другу.

К логарифмическому масштабу без особой необходимости прибегать не следует.

Одна из наиболее часто встречающихся погрешностей опыта - смещение нуля отсчета - приводит к сильному искажению прямолинейного характера кривой. В самом деле, пусть из-за смещения линейки вместо длин S на опыте будет найдено S₁ = S + а где, а - постоянная для всех точек ошибка. Формула, связывающая измеренную длину и время, в этом случае будет иметь вид S_t = (gt²/2) + а. В координатах S и t² эта зависимость изображается прямой линией, которая на этот раз не проходит через начало координат. По смещению прямой мы легко заметим ошибку и даже найдем ее величину. А в переменных lgS и lgt кривая теряет прямолинейный вид, и будет нелегко сообразить, где же вкралась ошибка.

Бывают, однако, случаи, когда логарифмический масштаб необходим. Это происходит, например, если исследуемая величина очень сильно изменяется, причем одновременно интересны очень малые и очень большие ее значения. Логарифмический масштаб позволяет все точки уместить на одном чертеже и исследовать совместно. Логарифмический масштаб выбирают и в том случае, если имеются основания ожидать, что искомая зависимость является степенной, но показатель степени неизвестен.

Определение искомых параметров по результатам измерений

Очень часто цель экспериментов заключается в том, чтобы из опыта найти неизвестный параметр в известной формуле.

Так, на Земле падение тел описывается формулой S = gt²/2, но величина g меняется от одного участка земной поверхности к другому и подлежит экспериментальному определению.

Радиоактивный распад подчиняется формуле

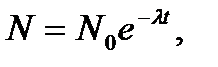
где N - количество атомов вещества в момент t, N₀ - начальное число атомов, а l - постоянная распада. Закон распада имеет один и тот же вид для всех ядер, но постоянная l у каждого из них своя и определяется экспериментально.

Растяжение тел описывается формулой

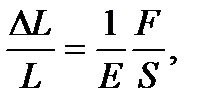
где L - длина образца, DL - его удлинение под действием силы F, S - площадь образца, E - константа (модуль упругости). Написанная формула - при небольших силах - описывает растяжение всех твердых тел, но величина модуля упругости зависит от материала, его обработки и т.д. Эта величина находится экспериментально. Пусть опыт состоит в определении модуля упругости. Экспериментатор измеряет L и S и записывает формулу в виде

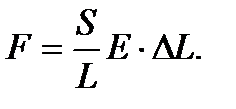
Затем тело растягивают и составляют таблицу зависимости удлинения от приложенной силы. Каждое из полученных значений, заносится в таблицу и определяет свое значение Е. Эти значения, из-за погрешностей опыта, несколько отличаются друг от друга. Нередко при обработке результатов, найденные таким образом значения модуля упругости усредняют. Это плохой и математически некорректный метод.

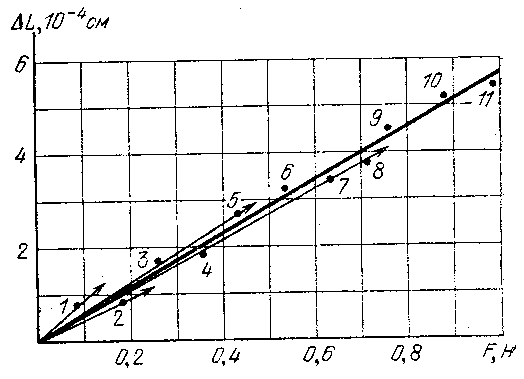
Поясним наше утверждение. На рисунке точками изображены результаты 11 опытов (разброс точек для наглядности увеличен). Первое из равенств соответствует прямой, проведенной из начала координат через точку 1. В самом деле, из этого равенства имеем

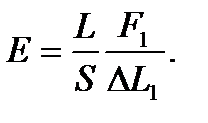
С точностью до постоянного для всех точек коэффициента пропорциональности L/S значение модуля упругости Е равно котангенсу угла, образованного осью абсцисс и прямой линией, проведенной из начала координат в эту точку. Второе из равенств соответствует прямой линии, проведенной через точку 2, и т.д. Усреднение величин Е, полученных во всех опытах, означает усреднение котангенсов указанных углов.

Рисунок показывает, однако, что усредняемые величины определяются из опыта с разной достоверностью. Точка 8 находится на расстоянии от наилучшей прямой (которая проведена жирной линией) не ближе, чем точка 3, но погрешность в определении угла для неё в несколько раз меньше. Обсуждаемый способ определения Е заключается, таким образом, в том, чтобы взять среднее из хороших и плохих результатов. Такая процедура, конечно, математически некорректна.

Иногда пытаются найти Е из прироста длины и силы на каждом шаге растяжения:

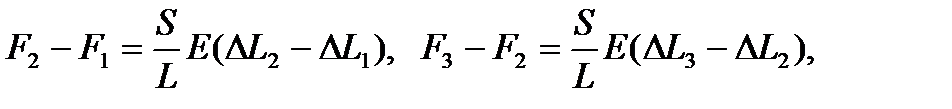и т. д.

При этом возникает много вычислительной работы и получается новый ряд значений Е, которые также чаще всего усредняют. И этот способ неправилен. Пусть, для примера, опыт ставится в условиях, когда все приращения длины равны друг другу. Тогда

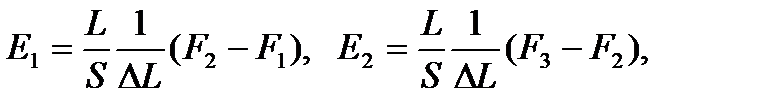и т. д.

При усреднении получим

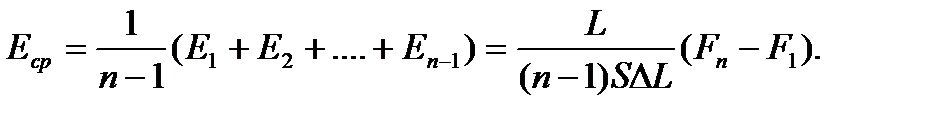
Таким образом, все найденные на опыте значения силы при усреднении сокращаются, и результат зависит только от первого и последнего опытов. Значит, при такой обработке мы на самом деле не усреднили результаты, полученные в разных опытах, а просто исключили из рассмотрения почти все полученные на опыте данные. Ясно, что такой метод нельзя признать разумным.

Математическая причина ошибок очевидна: разумно усреднять результаты только в том случае, если они являются равноточными и независимыми. В первом примере результаты обладали различной точностью, а во втором они не являются независимыми: одно и то же значение силы входит в два соседние равенства. Число примеров при желании можно было бы существенно увеличить.

Наиболее правильным и удобным методом обработки результатов является графический метод. Изобразим удлинения и силы на графике, как это и было сделано на рисунке. То есть, на этом рисунке проведена «наилучшая прямая», удовлетворяющая всем требованиям, которые обсуждались ранее. Наклон этой прямой соответствует изменению длины 5,7×10^{-4 см. при увеличении силы на 1 Н. Эта цифра может быть прямо подставлена в формулу для вычисления модуля упругости.}

При рекомендуемом методе графической обработки результатов - при проведении прямой на глаз - учитываются все точки графика. При этом точки, лежащие по его краям, оказываются более существенными, как это и должно быть. Математически этот способ эквивалентен методу «наименьших квадратов». Особым преимуществом графического метода является его простота.

Ещё одно замечание о построении таких графиков. Часто случается, что начальная точка искомой зависимости хорошо известна и лежит в начале координат.

Как бы ни была сложна зависимость тока, проходящего через проводник, от приложенного к нему напряжения, можно быть уверенным, что при отсутствии напряжения нет и тока (мы предполагаем, что в цепи не возникает термо-э.д.с., при отсутствии силы - нет удлинения, если тело не нагревать и не охлаждать, то изменение его температуры равно нулю, и т.д.).

Во всех этих случаях нулевая точка не просто известна, она является самой надежной из всех, которые используются при обработке результатов, а задача, проведения наилучшей прямой, сводится в этом случае к подбору параметра в формуле y=kx. В общем случае нужно найти параметры а и b в формуле y=a+bx.

Приведем правила для определения погрешностей, которые следует приписывать графически найденным параметрам прямой линии.

Пусть график прямой линии описывается формулой y=a+bx. Тогда, чтобы найти погрешность в определении параметра а нужно смещать прямую, параллельно самой себе, вниз, пока выше нее не окажется вдвое больше точек, чем снизу, затем следует сместить ее вверх, пока снизу не окажется вдвое больше точек, чем сверху. Если расстояние между этими прямыми равно Dа, то погрешность, определения а, равна 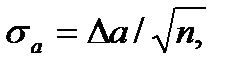где n - полное число точек на графике. Погрешность в определении параметра b находится аналогичным образом.