Электромагнитные поля в объемных резонаторах

Ни один радиоприемник, радиопередатчик, телевизор, лазер не обходиться без резонаторов. Резонатор в радиоэлектронной и лазерной технике – это электромагнитный маятник, в котором “качается” (колеблется) электромагнитная энергия. Частота колебаний определяется конструктивными, геометрическими и физическими параметрами резонатора. Самый первый и до настоящего времени остается распространенным LC- колебательный контур, внутри которого запасенная электромагнитная энергия периодически принимает форму энергии, то электрического поля то конденсатора, то магнитного поля катушки индуктивности.

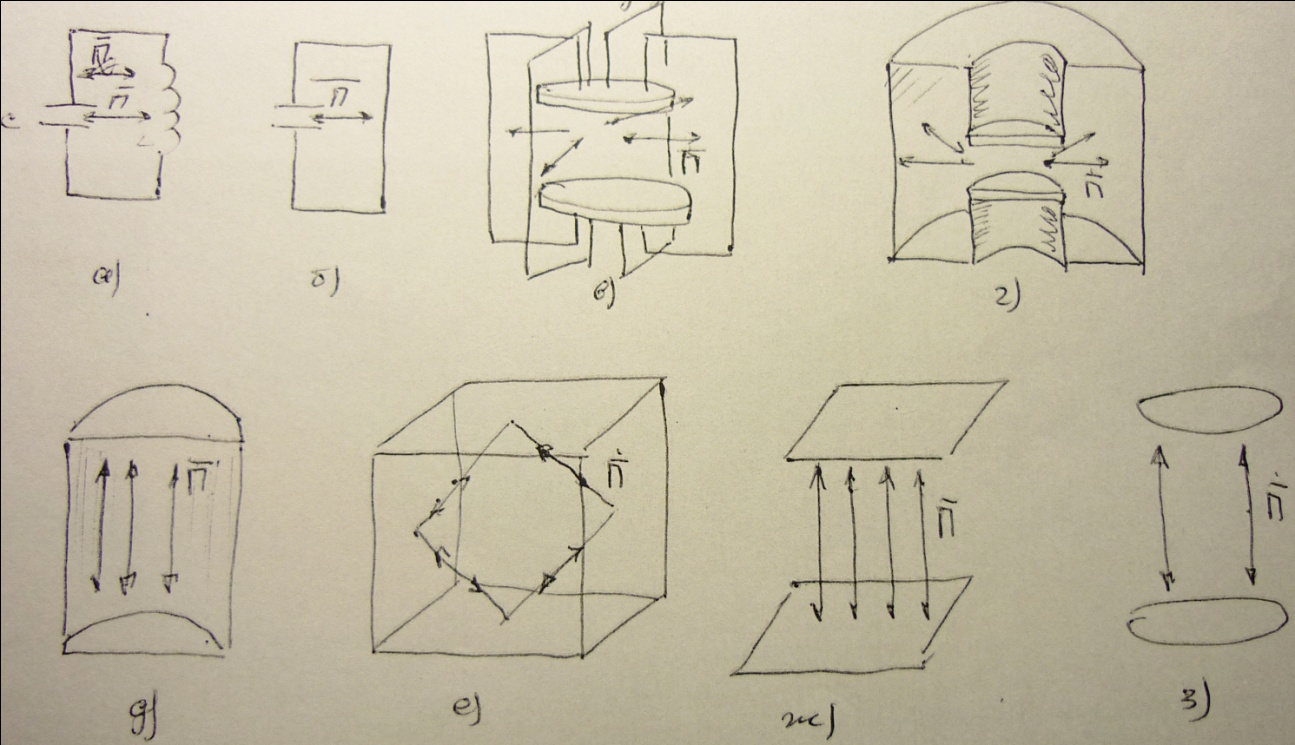
Стрелкой поперечного направления потока энергии- направление вектора Умова-Пойтинга. Частота колебаний определяется известной формулой .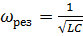

Увеличении резонансной частоты можно добиться, уменьшая L и С. На рис. б изображен контур с минимальной индуктивностью (один виток). Дальнейшее уменьшение L возможно подключенными параллельно последнему витку индуктивности дополнительных витков (рис. в). При этом резонатор остается открытым, поэтому его добротность падает из-за утечки электромагнитной энергии вследствие излучения. В пределе размещение дополнительных витков позволяет перейти к полностью закрытому резонатору, квазистационарного типа рис.2, широко распространенному дециметровом диапазоне волн. Если LC- резонатор состоит из сосредоточенных реактивностей L и С, то в квазистационарном резонаторе намечается переход к распределенным параметрам L и C. Дальнейшее повышение резонансной частоты достигается уменьшением С за счет емкостного зазора. Эта процедура завершается переходом к полому металлическому резонатору ( цилиндрическому или прямоугольному) рис. д и е. Полые металлические резонаторы не используются в качестве колебательных устройств “сантиметрового” и части “миллиметрового диапазонов волн. Размеры таких металлических резонаторов должны быть соизмеримы с длинной волны резонансных колебаний. Поэтому при освоении радиоэлектроникой оптического участка электромагнитного спектра из-за технологических трудностей потребовалось разработать новые колебательные устройства с реальными размерами, немного большими. Таким электромагнитным “маятником” оптического диапазона стали открытые резонаторы рис. ж, з, используя удалось создать лазеры –генераторы когерентного электромагнитного излучения оптического диапазона волн. Резонатором в СВЧ диапазоне может служить такие диэлектрическое тело в менее плотной среде (например в воздухе), если выполнены условия полного отражения на его границе.

Прямоугольный объемный резонатор

Его будем рассматривать как отрезок прямоугольного волновода определенной длины, на концах проводящими стенками. Для исследования волновода применим прямоугольную систему координат, и поле в резонаторе представим как результат наложения прямой и отраженной волны.

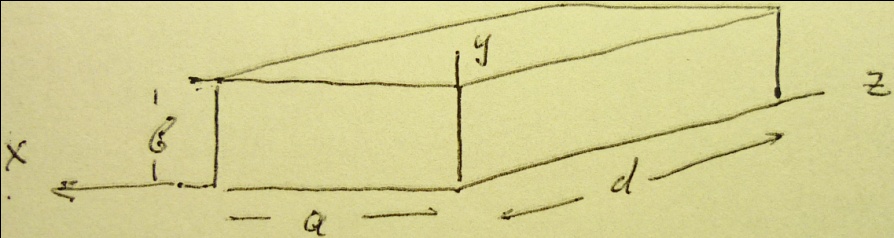
В резонаторе присутствует прямая и отраженная от стенок обратные волны. Выражение для поперечного электрического колебания TE имеет вид

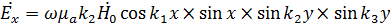
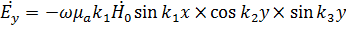
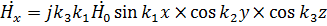(1)

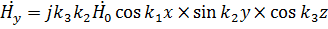
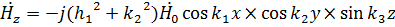
где 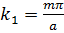; ; 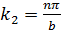; 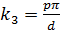где p=0,1,2,…

Картина поля в резонаторе подобна картине поля в волноводе, однако в резонаторе колебаниям соответствует стоячая волна, а в волноводе бегущая волна.

Из выражения (1) следует, что в прямоугольном объемном резонаторе может возбуждаться бесконечное число собственных колебаний (стоячих волн) T 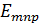, определяемых значениями индексов m, n, p. При этом m, n, p определяют число полуволн поля, укладывающихся на сторонах a и b соответственно, а индекс p- число полуволн поля, укладывающихся на длине резонатора d.Каждому колебанию соответствует длина волны и собственная частота:

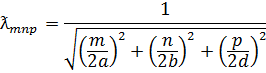
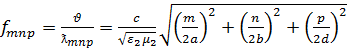(3)

Простейшие типы колебаний в прямоугольном объемном резонаторе

Из (3) следует, что наиболее низкая частота соответствует наименьшим значениям индексов m, n, p. Они не могут одновременно обращаться в ноль, так как в противном случае не может быть волн. Наименьшими значениями индексов, при которых выражение (1) не обращается в ноль следующие :

m=1 n=0 p=1

m=0 n=1 p=1

Таким образом, простейшими типами поперечно-электрических колебаний в прямоугольном объемном резонаторе являются 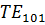и 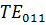волны. Этим колебаниям соответствуют собственные длины волн:

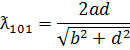
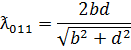
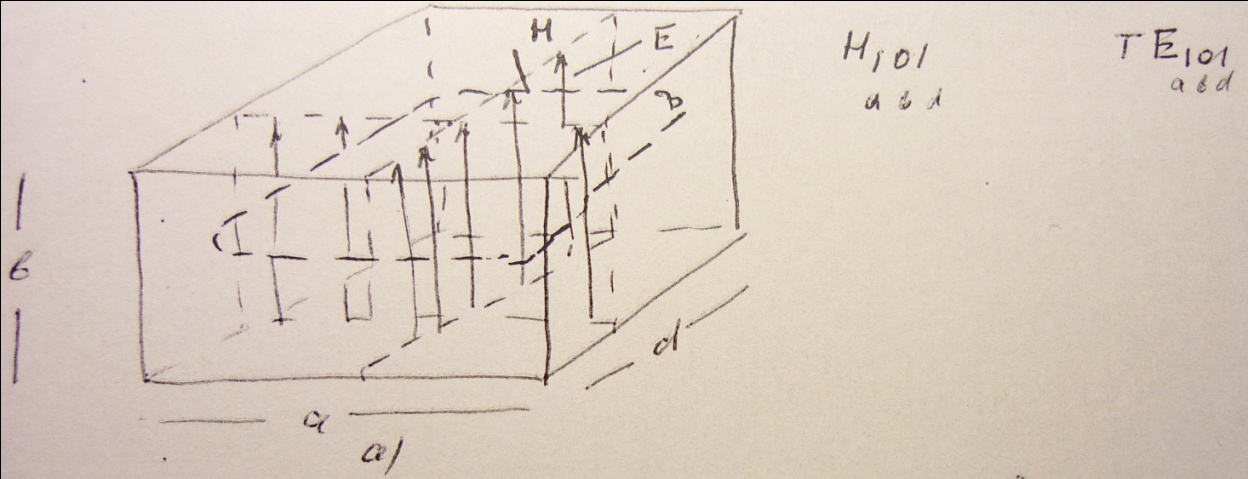
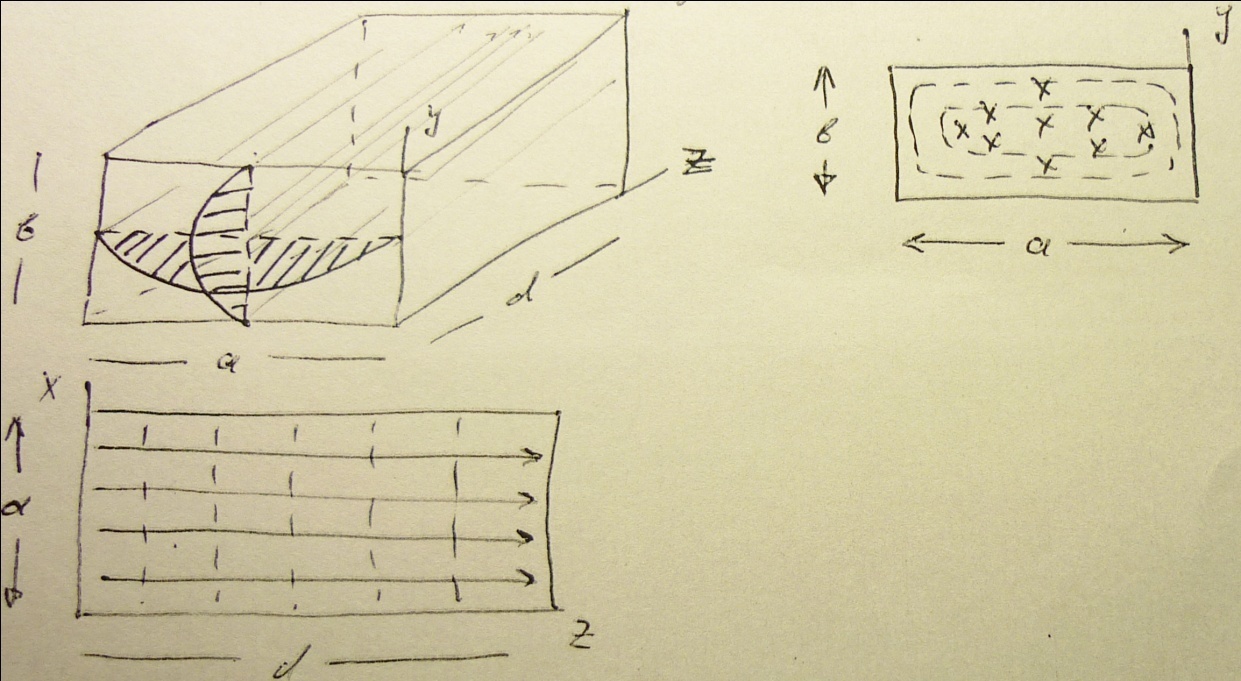
Картина поля 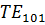( 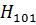) показана на (рис. а). Магнитные силовые линии замкнуты, летают в плоскостях параллельных основанию резонатора (axd) и охватывают силовые линии электрического поля.

Картина поля для 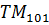приведена на (рис. в). Картина поля 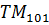аналогична картине поля 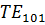. В общих случаях вектор 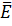параллелен одной из осей, а силовые линии магнитного поля расположены в плоскостях, перпендикулярных к этой оси. Таким образом картина полей колебаний типа 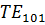, 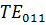и 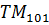одинаковы.