Круглый металлический волновод.

В круглом волноводе могут распространяться волны электрического 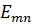и магнитного 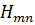типов. Решение задачи ищется в цилиндрической системе координат относительно продольной составляющей напряженности электрического поля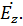

Уравнение Гельмгольца 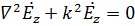в цилиндрической системе координат имеет вид :

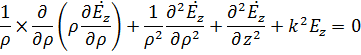
Решение этого уравнения является система

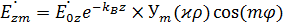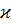, - каппа

где 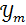- функция Бесселя первого рода m-ого порядка

k-волновое число в диэлектрике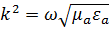

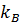-волновое число в волноводе

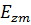-составляющая электрической напряженности на оси волновода.

,

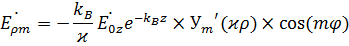
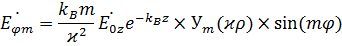
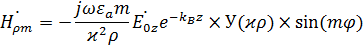
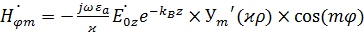где 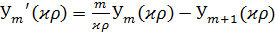- производная от функции Бесселя по аргументу .

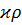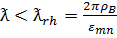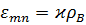Рабочая длина волны выбирается из условия , где -значение аргумента при которых функция Бесселя обращается в ноль. Из условия (1) следует, что наибольшая критическая длина волны соответствует тому типу волн , для которого 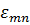-наименьшее. Этой волной является волна 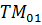( 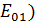. Критическая длина волны при этом будет:

.

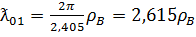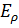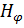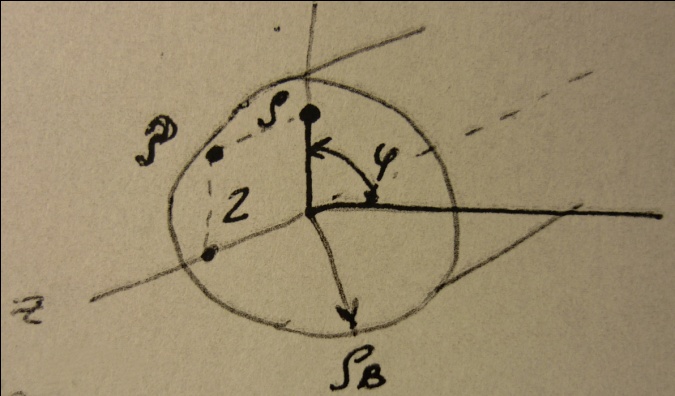
Составляющие и равны нулю на оси волновода и имеют максимальное значение при 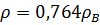. Магнитные силовые линии для волны типа 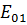представляют собой окружности, лежащие в поперечном сечении волновода. Электрические силовые линии расположены в плоскостях проведенных через радиусы и ось z (линии E). Поле рассматриваемой волны подобно полю волны 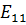в прямоугольном волноводе.