Качество процесса управления линейных САУ

1. Понятие качества процесса управления. Показатели качества переходного процесса в СУ и требования к ним

Анализ устойчивости системы не дает полной информации о характере переходного процесса в этой системе. Выясняется лишь сам факт устойчивости или неустойчивости исследуемой системы. Но для большинства систем автоматического управления этого недостаточно. Может оказаться, что система устойчива, то есть переходный процесс является затухающим, однако по характеру переходного процесса (например, большой колебательности) эту систему нельзя признать работоспособной. Разумеется, что требования к переходному процессу для различных систем будут отличаться, определяя различные процессы регулирования. Для одних систем может быть допустим колебательный характер переходного процесса, для других - только монотонный.

Поэтому качество процесса управления определяется поведением системы в переходном режиме.

Как известно, устойчивость линейной системы определяется только параметрами системы. Переходный процесс, в отличие от этого, зависит еще и от вида приложенного воздействия (управляющего или возмущающего), и от начальных условий. Причем внешние воздействия, прикладываемые к системе в реальных условиях, заранее не известны и очень часто носят случайный характер. Поэтому для сравнительной оценки динамики различных систем автоматического регулирования по переходному процессу выбираются типовые виды воздействия и определяется реакция системы при нулевых начальных условиях.

Для анализа качества переходного процесса обычно используется переходная функция (характеристика) системы, т.е. реакция системы при нулевых начальных условиях на единичную ступенчатую функцию. Действительно, внезапное подключение или сброс нагрузки, резкое изменение управляющего сигнала или возмущения носит ступенчатый характер, который является наиболее неблагоприятным. На рис.12.1 показана переходная функция системы.

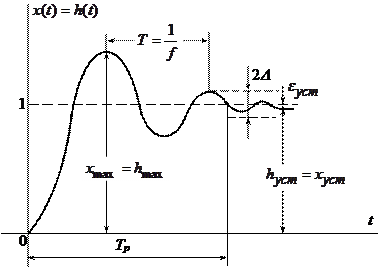Рис.12.1. Переходная функция САУ

Обычно рассматриваются следующие показатели качества.

1. Время регулирования (время переходного процесса) T_p – это время от момента приложения входного воздействия до момента, когда отклонение регулируемой величины относительно установившегося значения становится и остается по абсолютному значению меньше допустимой ошибки D. Задается величина D в процентах и допускается не более 10%.

2. Перерегулирование s - максимальное отклонение переходной характеристики от установившегося значения выходной величины, выраженное в относительных единицах или процентах:

.

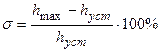Допустимое значение перерегулирования в каждом конкретном случае определяется требованиями и опытом эксплуатации системы, обычно 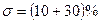. Иногда перерегулирование недопустимо совсем.

3. Частота колебаний 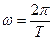, где T - период колебаний для колебательных характеристик.

4. Число колебаний m, которое имеет переходная функция h(t) за время регулирования Т_р. Число колебаний характеризует колебательность системы и при проектировании САУ чаще всего допускается m=1¸2, однако в некоторых случаях колебания в системе недопустимы.

5. Декремент затухания c, равный отношению модулей двух смежных перерегулирований

.

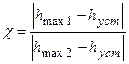Перечисленные показатели качества могут быть дополнены и другими, но это обусловливается спецификой проектируемой системы.

К показателям качества часто относят и установившуюся ошибку системы.

Графически требования к показателям качества переходного процесса по пунктам 1 и 2 определяются областью, изображенной на рис.12.2. Система автоматического регулирования будет обладать требуемыми показателями качества, если ее переходная характеристика не выйдет за пределы указанной области.

По своему характеру переходные процессы делятся на следующие основные типы (рис.12.3).

1. Колебательные процессы (кривая 1) характеризуются наличием двух или большего числа колебаний регулируемой величины относительно ее установившегося значения за время переходного процесса.

2. Малоколебательные процессы (кривая 2) характеризуются наличием лишь одного колебания регулируемой величины относительно ее установившегося значения за время переходного процесса.

3. Процессы без перерегулирования (кривая 3) характеризуются тем, что регулируемая величина не меняет знака, а ее производная меняет знак в переходном процессе.

4. Монотонные процессы (кривая 4) характеризуется тем, что производная от регулируемой величины не меняет знака в переходном процессе.

Рассмотренные типы переходных процессов определяются решением соответствующих дифференциальных уравнений, описывающих поведение реальной системы. При этом следует иметь в виду, что знание корней характеристического уравнения САУ, особенно для системы высокого порядка, еще недостаточно для полного суждения о кривой переходного процесса, если неизвестны начальные условия, перечисленные с учетом внешнего воздействия.

Для построения кривой переходного процесса необходимо решить дифференциальное уравнение, описывающее состояние системы. Так как системы автоматического управления описываются дифференциальными уравнениями высокого порядка, то решение этих уравнений связано с большими вычислительными трудностями. Поэтому на практике широко используются приближенные методы решения этих уравнений. Наиболее известным приближенным методом решения дифференциальных уравнений применительно к задачам анализа автоматического регулирования является численно-графический метод, разработанный Башкировым.

Наряду с прямыми способами вычисления переходного процесса систем автоматического регулирования, связанными с непосредственным решением соответствующих дифференциальных уравнений, используются косвенные методы, которые позволяют в более простой и удобной форме оценивать качества переходного процесса.

Следует отметить, что косвенные методы не дают полной информации о переходном процессе, а характеризуют лишь отдельные его стороны. Для многих практических задач этого вполне достаточно. Среди косвенных методов оценки переходного процесса широко используются следующие:

− метод интегральных оценок;

− корневые методы;

− частотные методы.

2. Управляемость и наблюдаемость

Управляемость

Для решения задач управления важно знать, обладает ли объект свойством управляемости в смысле возможности его перевода из заданной начальной точки (или области) в заданную конечную точку (или область). Выше при рассмо­трении задач оптимального управления предполагалось, что объект таким свойством обладает, иначе не имело бы смысла ставить эти задачи. Кроме того, обычно разработчик, выбирая структуру системы управления, прежде всего заботится о том, чтобы то, что мы называем объектом управления, обладало свойством управляемости, и делает он это на основе инженер­ных знаний и опыта. Но в сложных случаях не исключена ошибка в выборе структуры системы управления, из-за чего объект не будет обладать указанным свойством. Поэтому воз­никает проблема управляемости — проблема установления обладания объектом свойства управляемости. Эта проблема впервые была поставлена лишь во второй половине нашего века.

Перейдем к строгому определению свойства управляемо­сти объекта и установлению критерия управляемости.

Пусть объект задается уравнением

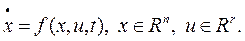
Здесь пока принимается, что допустимое множество U_t зна­чений управления совпадает со всем пространством R^r и до­пустимым управлением является любая кусочно-непрерыв­ная вектор-функция, принимающая значения из R^r.

Объект называется вполне или полностью управляемым, если для любой пары точек х⁰ и х^f из Rⁿ существует допусти­мое управление на конечном интервале [t₀, t_f], переводящее объект из точки х(t₀)=х⁰ в точку х(t_f)=х^f.

В случае стационарного объекта всегда можно принять t₀=0. Если объект является линейным, т. е. задается урав­нением вида

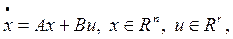(12.1)

в приведенном определении можно одну из точек х⁰ или х^f зафиксировать, например положить х⁰=0 или х^f=0. Дей­ствительно, так как решение (12.1) при произвольном на­чальном условии х(t₀)=х⁰ имеет вид

,

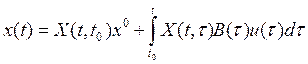и при х(t₀)=0

,

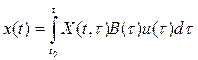то задача перевода объекта (12.1) из произвольной начальной точки х(t₀)=х⁰ в точку х(t_f)=х^f равносильна задаче его перевода из начальной точки х(t₀)=0 в точку х(t_f)=х^f-X(t_f,t₀)x⁰ .Аналогично, задача перевода объекта (12.1) из начальной точки х(t₀)=х⁰ в произвольную конечную точ­ку х(t_f)=х^f равносильна задаче его перевода из начальной точки х(t₀)=х⁰-X^-1(t_f,t₀)x(t_f) в точку х(t_f)=0. Та­ким образом, в случае линейного объекта свойство управляе­мости можно еще определить следующим образом: объект (12.1) называется вполне управляемым, если для любой точки х^f из Rⁿ существует допустимое управление на конечном интер­вале [t₀, t_f], переводящее объект из точки х(t₀)=0 в точку х(t_f)=х^f, или объект (12.1) называется вполне управляе­мым, если для любой точки х⁰ из Rⁿ существует допустимое управление на конечном интервале[t₀, t_f], переводящее объект из точки х(t₀)= х⁰ в точку х(t_f)=0.

Управляемость линейных стационарных объектов. Пусть матрица А и В в (10.83) постоянны. Введем в рассмотрение так называемую матрицу управляемости

У=[В АВ А²B... А^n-1B], (12.2)

которая состоит из столбцов матрицы В и произведений ма­триц АВ, А²В, ....А^n-1B и имеет размерность (п x nr). Справедлив следующий критерий управляемости: линейный стационарный объект (12.1) вполне управляем тогда и толь­ко тогда, когда ранг матрицы управляемости (12.2) равен п.

Наблюдаемость линейных стационарных систем. Рассмотрим линейную стационарную систему

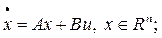(12.3)

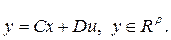(12.4)

Введем так называемую матрицу наблюдаемости

Н=[С^ТA^ТС^Т... (A^Т)^n-1C^T]. (12.5)

Эта матрица состоит из столбцов матрицы C^T, произведений матриц A^ТС^Т, (A^Т)²C^T, ..., (A^Т)^n-1C^T и имеет размерность (п x ρn).

Для линейной стационарной системы справедлив следую­щий критерий полной наблюдаемости: система (12.3), (12.5), вполне наблюдаема (восстанавливаема) тогда и только тогда, когда ранг матрицы наблюдаемости (12.5) равен п.

Транспонированная матрица

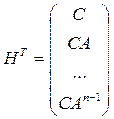(12.6)

имеет такой же ранг, что и матрица (12.5), поэтому вместо исходной матрицы наблюдаемости можно рассматривать транспонированную. Ниже приводится доказательство критерия наблюдаемости.