Обработка экспериментальных данных подчиняющихся нормальному закону распределения

Если итоги проверки массива по 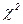не противоречат гипотезе, то можно считать, что среднее арифметическое значение результата измерения тоже подчиняется нормальному закону. А среднее значение среднего арифметического равно среднему значению:

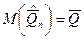
Ни одно из случайных значений подчиняющихся нормальному закону распределения не может отличаться от среднего больше чем на ½ доверительного интервала:

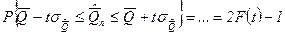
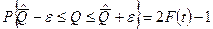Заменяя среднее квадратичное отклонение среднего арифметического его оценкой получим , где .

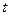выбирается для заданной доверительной вероятности по функции Лапласа.

При небольшом объеме экспериментальных данных среднее арифметическое результата измерения, подчиняющегося нормальному закону, само подчиняется распределению вероятности Стьюдента, с тем же средним значением.

Для критерия Стьюдента имеются графики. При 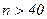график сливается с функцией Лапласа.

Доверительная вероятность того, что любое случайное значение среднего арифметического подчиняется закону распределения Стьюдента не отличающееся больше чем на ½ доверительного интервала.

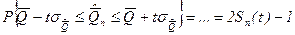, где 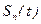- интегральная функция распределения Стьюдента.

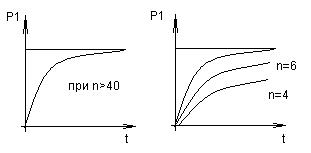
При 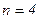вероятность того, что никакое значение среднего арифметического подчиняющегося закону распределения Стьюдента не отличается от среднего больше чем на 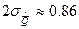; при .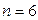

При совсем незначительном количестве экспериментальных данных 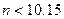и принятой гипотезе о нормальности закона распределения выявление ошибок по правилу 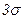не проводится.