Поле преобразователя произвольной формы
Будем считать длительность акустических импульсов настолько большой, что колебания во время импульса можно считать непрерывными. В то же время длительность импульса достаточно коротка для того, чтобы прием и излучение колебаний происходили в разные промежутки времени. В этом случае поле излучения может быть представлено как результат действия множества точечных излучателей на поверхности пьезопластины произвольной формы (рис. 2.1).
На данной схеме пьезопластина прижата к горизонтальной поверхности объекта контроля. Поверхность излучающей пьезопластины представлена как совокупность точечных источников ультразвука. Поле элементарного источника А, имеющего сферический фронт, запишется в виде выражения
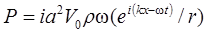 , (2.2)
, (2.2)
где P – акустическое давление;
а – радиус источника (очень мал);
r – плотность среды;
r – радиус фронта.
Пусть dSA – элемент пластины (источника), тогда его можно выразить через площадь излучающей полусферы
dSA = 2p а2 . (2.3)
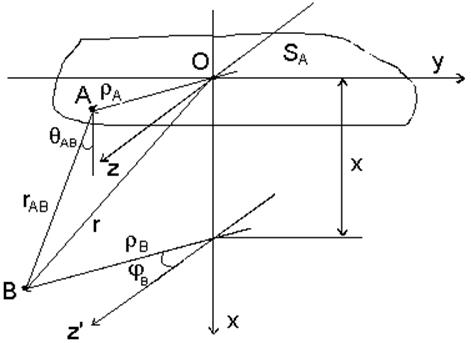
Рис. 2.1. Схема для расчета поля излучения преобразователя произвольной формы: А – элементарный источник; В – произвольная точка среды; SА – площадь источника; 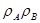 – радиус-вектор; φB – угол между осью Oz’ и радиус-вектором; r – радиус фронта;qАВ – угол между rАВ и нормалью к поверхности пьезопластины; rАВ – расстояние от точки А преобразователя до точки В элементарного отражателя в объекте контроля
– радиус-вектор; φB – угол между осью Oz’ и радиус-вектором; r – радиус фронта;qАВ – угол между rАВ и нормалью к поверхности пьезопластины; rАВ – расстояние от точки А преобразователя до точки В элементарного отражателя в объекте контроля
Акустическое давление в точке В:
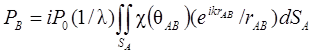 , (2.4)
, (2.4)
где p0 – давление в точке А (на границе полусферы);
IAB – распределение поля давления;
c(qАВ) – множитель, характеризующий направленность излучения
элементарного источника:
- при излучении в жидкости в отсутствие сдвига c(qАВ)=cos(qАВ);
- при излучении в твердую среду c(qАВ)»1при qАВ£60°;
- c(qАВ)=0 при qАВ>60°. В этом случае амплитуда оказывается малой;
- для прямых преобразователей считают, что c= 0.
Формула справедлива в случае rАВ >>l, т. е. в случае рассмотрения ультразвукового поля в дальней зоне. Уравнение не учитывает ни формы, ни длительности акустического импульса.
Поле приема – это зависимость амплитуды от координаты точки, в которой расположен приемник. Пусть излучение точечного источника В принимается точечным приемником А (рис. 2.1):
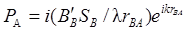 ,
,
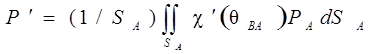 , (2.5)
, (2.5)
где P' – среднее давление
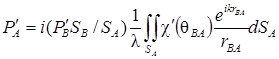 , (2.6)
, (2.6)
c' – характеризует чувствительность точечного приемника А, которая зависит от направления падающей волны. c' » 1вблизи акустической оси преобразователя. Из сравнения (2.4) и (2.5) видно, что подынтегральные выражения в уравнениях поля излучения и поля приема совпадают с точностью до множителей c и c', следовательно, поле излучения и поле приема пропорциональны. То есть P'А~PB .
Можно обозначить поле излучения-приема в общем виде
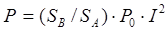 , (2.7)
, (2.7)
где I – подынтегральное выражение для совмещенного преобразователя;
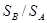 – коэффициент пропорциональности, учитывающий отношение площади излучателя к площади преобразователя;
– коэффициент пропорциональности, учитывающий отношение площади излучателя к площади преобразователя;
P0 – амплитуда давления в режиме излучения.
Если SA=SB , то можно говорить об одном поле – поле излучения-приема.
Для расчета акустического поля преобразователей различной формы (типа) необходимо прежде всего проанализировать функцию I.
Дата добавления: 2015-12-10; просмотров: 1677;
