Для друзей математики

Среди читателей этой книги, без сомнения, найдутся и такие, которые пожелают сами проверить расчеты, упомянутые выше. Приводим здесь эти вычисления. Они верны лишь приблизительно, так как основаны на допущении, что в канале пушки снаряд движется равномерно‑ускоренно (в действительности же возрастание скорости происходит неравномерно).

Для расчетов придется пользоваться следующими двумя формулами равномерно‑ускоренного движения:

скорость v по истечении t‑й секунды равна at, где а – ускорение:

v = at;

путь S, пройденный за t секунд, определяется формулой

S = at²/2.

По этим формулам определим прежде всего ускорение снаряда, когда он скользил в канале «колумбиады».

Из романа известна длина части пушки, не занятой зарядом, – 210 м; это и есть пройденный снарядом путь S.

Мы знаем и конечную скорость: v = 16 000 м/сек. Данные S и v позволяют определить величину t – продолжительность движения снаряда в канале орудия (рассматривая это движение как равномерно‑ускоренное). В самом деле:

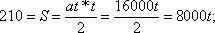
v = at = 16000,

откуда

t = 210/8000 = около 1/40 сек.

Снаряд, оказывается, скользил бы внутри пушки всего 1/40 секунды! Подставив

t = 1/40 в формулу v = at, имеем:

16 000 = 1/40 a, откуда a = 640 000 м/сек².

Значит, ускорение снаряда при движении в канале равно 640 000 м/сек², т. е. в 64 000 раз больше ускорения силы тяжести!

Какой же длины должна быть пушка, чтобы ускорение снаряда было всего в 10 раз больше ускорения падающего тела (т. е. равнялось бы 100 м/сек²)?

Это – задача, обратная той, которую мы сейчас решили. Данные:

a = 100 м/сек²,

v = 11 000 м/сек (при отсутствии сопротивления атмосферы такая скорость достаточна).

Из формулы v = at имеем:

11000 = 100t, откуда t = 110 сек.

Из формулы S = at²/2 = at×t/2 получаем, что длина пушки должна равняться

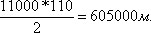
т. е. круглым счетом 600 км.

Такими вычислениями получены те цифры, которые разрушают заманчивые планы героев Жюля Верна[31].

Глава шестая