Уничтоженная» тяжесть

«Вода не выливается из сосуда, который вращается, – не выливается даже тогда, когда сосуд перевернут дном вверх, ибо этому мешает вращение», – писал две тысячи лет назад Аристотель. На рис. 32 изображен этот эффектный опыт, который, без сомнения, многим знаком: вращая достаточно быстро ведерко с водой, как показано на рисунке, вы достигаете того, что вода не выливается даже в той части пути, где ведерко опрокинуто вверх дном.

В обиходе принято объяснять это явление «центробежной силой», понимая под нею ту воображаемую силу, которая будто бы приложена к телу и обусловливает стремление его удалиться от центра вращения. Этой силы не существует: указанное стремление есть не что иное, как проявление инерции, а всякое движение по инерции осуществляется без участия силы. В физике под центробежной силой разумеют нечто иное, а именно – ту реальную силу, с какой вращающееся тело натягивает удерживающую его нить или давит на свой криволинейный путь. Сила эта приложена не к движущемуся телу, а к препятствию, мешающему ему двигаться прямолинейно: к нити, к рельсам на кривом участке пути и т. п.

Обращаясь к вращению ведерка, попытаемся разобраться в причине этого явления, не прибегая вовсе к двусмысленному понятию «центробежной силы». Зададим себе вопрос: куда направится струя воды, если в стенке ведерка сделать отверстие? Не будь силы тяжести, водяная струя по инерции направилась бы по касательной AK к окружности AB (рис. 32). Тяжесть же заставляет струю снижаться и описывать кривую (параболу AP). Если окружная скорость достаточно велика, эта кривая расположится вне окружности AB. Струя обнаруживает перед нами тот путь, по которому при вращении ведерка двигалась бы вода, если бы не препятствовало надавливающее на нее ведерко. Теперь понятно, что вода вовсе не стремится двигаться отвесно вниз, а потому и не выливается из ведерка. Она могла бы вылиться из него лишь в том случае, если бы ведерко было обращено отверстием в направлении его вращения.

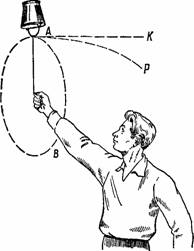
Рисунок 32. Почему не выливается вода из вращаемого ведерка?

Вычислите теперь, с какой скоростью надо в этом опыте вращать ведерко, чтобы вода из него не выливалась вниз. Скорость эта должна быть такова, чтобы центростремительное ускорение вращающегося ведерка было не меньше ускорения силы тяжести: тогда путь, по которому стремится двигаться вода, будет лежать вне окружности, описываемой ведерком, и вода нигде от ведерка не отстанет. Формула для вычисления центростремительного ускорения W такова:

W = v²/R,

где v – окружная скорость, R – радиус кругового пути. Так как ускорение тяжести на земной поверхности g = 9,8 м/сек², то имеем неравенство v²/R >= 9,8. Если положить R равным 70 см, то

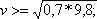
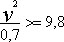
и v >= 2,6 м/сек.

Легко рассчитать, что для получения такой окружной скорости надо делать рукой около полутора оборотов в секунду. Подобная быстрота вращения вполне достижима, и опыт удается без труда.

Способностью жидкости прижиматься к стенкам сосуда, в котором она вращается вокруг горизонтальной оси, пользуются в технике для так называемого центробежного литья. При этом имеет существенное значение то, что неоднородная жидкость расслаивается по удельному весу: более тяжелые составные части располагаются дальше от оси вращения, легкие занимают место ближе к оси. Вследствие этого все газы, содержащиеся в расплавленном металле и образующие так называемые «раковины» в литье, выделяются из металла во внутреннюю, полую часть отливки. Изделия, изготовленные таким способом, получаются плотные и свободные от раковин. Центробежное литье дешевле обычного литья под давлением и не требует сложного оборудования.

Вы в роли Галилея

Для любителей сильных ощущений иногда устраивается весьма своеобразное развлечение – так называемая «чертова качель». Имелась такая качель и в Ленинграде. Мне не пришлось самому на ней качаться, а потому приведу здесь ее описание из сборника научных забав Федо:

«Качель подвешена к прочной горизонтальной перекладине, перекинутой через комнату на известной высоте над полом. Когда все сядут, особо приставленный к этому служитель запирает входную дверь, убирает доску, служившую для входа, и, заявив, что он сейчас даст возможность зрителям сделать небольшое воздушное путешествие, начинает легонько раскачивать качель. Вслед за тем он садится назади качели, подобно кучеру на запятках, или совсем выходит из зала.

Между тем размахи качели становятся все больше и больше; она, по‑видимому, поднимается до высоты перекладины, потом переходит за нее, выше и выше и, наконец, описывает полный круг. Движение ускоряется все заметнее, и качающиеся, хотя по большей части уже предупрежденные, испытывают несомненные ощущения качания и быстрого движения; им кажется, что они несутся вниз головой в пространстве, так что невольно хватаются за спинки сидений, чтобы не упасть.

Но вот размахи начинают уменьшаться; качель более не поднимается уже на высоту перекладины, а еще через несколько секунд останавливается совершенно.

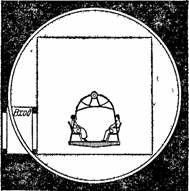
Рисунок 33. Схема устройства «чертовой качели».

На самом же деле качель все время висела неподвижно, пока продолжался опыт, а сама комната, с помощью очень несложного механизма, обращалась мимо зрителей вокруг горизонтальной оси. Разного рода мебель прикреплена к полу или стенам зала; лампа, припаянная к столу так, что она, по‑видимому, легко может перевернуться, состоит из электрической лампочки накаливания, скрытой под большим колпаком. Служитель, который, по‑видимому, раскачивал качель, давая ей легкие толчки, в сущности, сообразовал их с легкими колебаниями зала и делал только вид, что раскачивает. Вся обстановка способствует полному успеху обмана».

Секрет иллюзии, как видите, прост до смешного. И все‑таки, если бы теперь, уже зная, в чем дело, вы очутились на «чертовой качели», вы неизбежно поддались бы обману. Такова сила иллюзии!

Помните стихотворение Пушкина «Движение»?

– Движенья нет, – сказал мудрец брадатый[13].

Другой[14]смолчал – и стал пред ним ходить.

Сильнее бы не мог он возразить.

Хвалили все ответ замысловатый.

Но, господа, забавный случай сей

Другой пример на память мне приводит:

Ведь каждый день над нами Солнце ходит,

Однако ж прав упрямый Галилей!

Среди пассажиров качели, не посвященных в ее секрет, вы были бы своего рода Галилеем – только наоборот: Галилей доказывал, что Солнце и звезды неподвижны, а кружимся, вопреки очевидности, мы сами; вы же будете доказывать, что неподвижны мы, а вся комната вертится вокруг нас. Возможно, что вам пришлось бы при этом испытать и печальную участь Галилея; на вас смотрели бы, как на человека, спорящего против очевидных вещей…

Мой спор с вами

Доказать свою правоту вам будет не так легко, как вы, может быть, полагаете. Вообразите, что вы в самом деле очутились на «чертовой качели» и хотите убедить ваших соседей, что они заблуждаются. Предлагаю вам вступить в этот спор со мной. Сядем с вами на «чертову качель», дождемся момента, когда, раскачавшись, она начнет, по‑видимому, описывать полные круги, и заведем диспут о том, что кружится: качель или вся комната? Прошу только помнить, что во время спора мы не должны покидать качели; все необходимое захватим с собой заблаговременно.

Вы . Как можно сомневаться в том, что мы неподвижны, а вертится комната! Ведь если бы нашу качель в самом деле опрокинуть вверх дном, то мы с вами не повисли бы вниз головой, а выпали бы из нес. Но мы не падаем. Значит, вертится не качель, а комната.

Я . Однако вспомните, что вода из быстро кружащегося ведерка не выливается, хотя оно и опрокидывается вверх дном (стр. 55). Велосипедист в «чертовой петле» (см. далее, стр. 65) также не падает, хотя и едет вниз головой.

Вы . Если так, то вычислим центростремительное ускорение и убедимся, достаточно ли оно для того, чтобы мы не выпали из качели. Зная наше расстояние от оси вращения и число оборотов в секунду, мы легко определим по формуле…

Я . Не трудитесь вычислять. Устроители «чертовой качели», зная о нашем споре, предупредили меня, что число оборотов будет вполне достаточно, чтобы явление объяснялось по‑моему. Следовательно, вычисление не решит нашего спора.

Вы . Однако я не потерял надежды вас переубедить. Видите, вода из этого стакана не выливается на пол… Впрочем, вы и тут сошлетесь на опыт с вращающимся ведерком. Хорошо же: я держу в руке отвес, – он все время направлен к нашим ногам, т. е. вниз. Если бы вертелись мы, а комната оставалась неподвижной, отвес был бы все время обращен к полу, т. е. вытягивался бы то к нашим головам, то вбок.

Я . Ошибаетесь: если мы вертимся с достаточной скоростью, то отвес все время должен отбрасываться от оси вдоль радиуса вращения, т. е. к нашим ногам, как мы и наблюдаем.

Финал нашего спора

Теперь позвольте вам посоветовать, как одержать победу в этом споре. Надо взять с собою на «чертову качель» пружинные весы, положить на их чашку гирю, например в 1 кг, и следить за положением указателя: он все время будет показывать один и тот же означенный на гире вес, именно – один килограмм. Это и есть доказательство неподвижности качели.

В самом деле: если бы мы вместе с пружинными весами описывали круги около оси, то на гирю, кроме силы тяжести, действовал бы также центробежный эффект, который в нижних точках пути увеличивал бы вес гири, а в верхних уменьшал бы его; мы должны были бы замечать, что гиря то становится тяжелее, то почти ничего не весит. А раз этого не замечается, значит, вращается комната, а не мы.