В «заколдованном» шаре

Один предприниматель в Америке устроил для развлечения публики очень забавную и поучительную карусель в форме шарообразной вращающейся комнаты. Люди внутри нее испытывают такие необыкновенные ощущения, какие мы считаем возможными разве только во сне или в волшебной сказке.

Вспомним сначала, что испытывает человек, стоящий на быстро вращающейся круглой платформе.

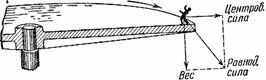
Рисунок 34. Что испытывает человек на краю вращающейся платформы.

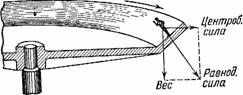
Рисунок 35. Человек прочно стоит на наклонном конце вращающейся платформы.

Вращательное движение стремится отбросить человека наружу; чем дальше стоите вы от центра, тем сильнее будет клонить и тянуть вас наружу. Если закроете глаза, вам будет казаться, что вы стоите не на горизонтальном полу, а на наклонной плоскости, на которой с трудом сохраняете равновесие. Это станет понятно, когда рассмотрим, какие силы действуют здесь на наше тело (рис. 34). Действие вращения увлекает наше тело наружу, тяжесть тянет вниз; оба движения, складываясь по правилу параллелограмма, дают результирующее действие, которое наклонено вниз. Чем быстрее вращается платформа, тем это результирующее движение больше и направляется более отлого.

Представьте же себе теперь, что край платформы загнут вверх и вы стоите на этой отогнутой наклонной части (рис. 35). Если платформа неподвижна, вы в таком положении не удержитесь, а сползете или даже опрокинетесь. Другое дело, если платформа вращается: тогда эта наклонная плоскость станет для вас, при известной скорости, как бы горизонтальной, потому что результирующее обоих увлекающих вас движений направится тоже наклонно, под прямым углом к отогнутой части платформы[15].

Если вращающейся платформе придать такую кривизну, чтобы при определенной скорости ее поверхность была в каждой точке перпендикулярна к результирующей, то помещенный на пол человек будет чувствовать себя во всех ее точках, как на горизонтальной плоскости. Математическим вычислением найдено, что такая кривая поверхность есть поверхность особого геометрического тела – параболоида. Ее можно получить, если быстро вращать вокруг вертикальной оси стакан, до половины налитый водой: тогда вода у краев поднимется, в центре опустится, и поверхность ее примет форму параболоида.

Если вместо воды налить в стакан растопленный воск и продолжать вращение до тех пор, пока воск не остынет, то затвердевшая поверхность его даст нам точную форму параболоида. При определенной скорости вращения такая поверхность является для тяжелых тел как бы горизонтальной: шарик, положенный в любую ее точку, не скатывается вниз, а остается на этом уровне (рис. 36).

Теперь легко будет понять устройство «заколдованного» шара.

Дно его (рис. 37) составляет большая вращающаяся платформа, которой придана кривизна параболоида. Хотя вращение благодаря скрытому под платформой механизму совершается чрезвычайно плавно, все же люди на платформе испытывали бы головокружение, если бы окружающие предметы не перемещались вместе с ними; чтобы не дать возможности наблюдателю обнаружить движение, платформу помещают внутри большого шара с непрозрачными стенками, который вращается с такой же скоростью, как и сама платформа.

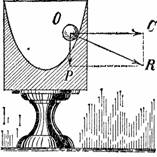
Рисунок 36. Если этот бокал вращать с достаточной скоростью, то шарик не скатится на его дно.

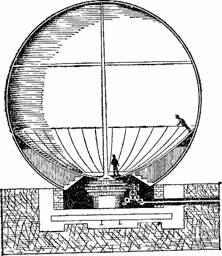
Рисунок 37. «Заколдованный» шар (разрез).

Таково устройство этой карусели, носящей название «заколдованной» или «волшебной» сферы. Что же испытываете вы, находясь на платформе внутри сферы? Когда она вращается, пол под вашими ногами горизонтален, в какой бы точке кривой платформы вы ни находились, – у оси, где пол действительно горизонтален, или у края, где он наклонен на 45°. Глаза ясно видят вогнутость, мускульное же чувство свидетельствует, что под вами ровное место.

Показания обоих чувств противоречат друг другу самым резким образом. Если вы перейдете с одного края платформы на другой, то вам покажется, будто весь огромный шар с легкостью мыльного пузыря перевалился на другой бок под тяжестью вашего тела: ведь во всякой точке вы чувствуете себя, как на горизонтальной плоскости. А положение других людей, стоящих на платформе наклонно, должно представляться вам до крайности необычайным: вам буквально будет казаться, что люди, как мухи, ходят по стенам (рис. 39).

Вода, вылитая на пол заколдованного шара, растеклась бы ровным слоем по его кривой поверхности. Людям казалось бы, что вода здесь стоит перед ними наклонной стеной.

Привычные представления о законах тяжести словно отменяются в этом удивительном шаре, и мы переносимся в сказочный мир чудес…

Подобные ощущения испытывает на поворотах летчик. Так, если он летит со скоростью 200 км в час по кривой с радиусом 500 м, то земля должна казаться[16]ему приподнявшейся и наклоненной на 16°.

Рисунок 38. Истинное положение людей внутри «заколдованною» шара.

Рисунок 39. Положение, которое представляется при этом каждому из двух посетителей.

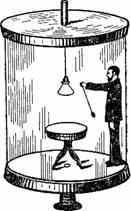
Рисунок 40. Вращающаяся лаборатория – действительное положение.

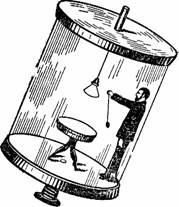
Рисунок 41. Кажущееся положение той же вращающейся лаборатории.

В Германии, в городе Геттингене, была сооружена для научных изысканий подобная вращающаяся лаборатория. Это (рис. 40) цилиндрическая комната 3 м в поперечнике, вращающаяся со скоростью до 50 оборотов в секунду. Так как пол комнаты плоский, то при вращении наблюдателю, стоящему у стены, кажется, будто комната откинулась назад, а сам он полулежит на покатой стене (рис. 41).

Жидкий телескоп

Наилучшая форма для зеркала отражательного телескопа – параболическая, т. е. именно та форма, какую сама собою принимает поверхность жидкости во вращающемся сосуде. Конструкторы телескопов затрачивают много хлопотливого труда, чтобы придать зеркалу подобную форму. Изготовление зеркала для телескопа длится целые годы. Американский физик Вуд обошел эти затруднения, устроив жидкое зеркало: вращая ртуть в широком сосуде, он получил идеальную параболическую поверхность, которая могла играть роль зеркала, так как ртуть хорошо отражает лучи света. Телескоп Вуда был установлен в неглубоком колодце.

Недостаток телескопа, однако, тот, что малейший толчок морщит поверхность жидкого зеркала и искажает изображение, а также и тот, что горизонтальное зеркало дает возможность непосредственно рассматривать только те светила, которые находятся в зените.

«Чертова петля»

Быть может, вам знаком головокружительный велосипедный трюк, иногда исполняемый в цирках: велосипедист едет в петле снизу вверх и описывает полный круг, несмотря на то, что по верхней части круга ему приходится ехать вниз головой. На арене устраивают деревянную дорожку в виде петли с одним или несколькими завитками, как изображено на нашем рис. 42. Артист спускается на велосипеде по наклонной части петли, затем быстро взлетает на своем стальном коне вверх, по круговой ее части, совершает полный оборот, буквально вниз головой, и благополучно съезжает на землю[17].

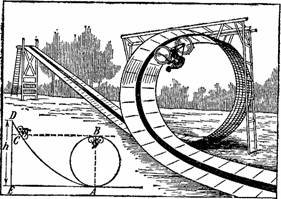
Рисунок 42. «Чертова петля». Внизу слева – схема для расчета.

Этот головоломный велосипедный фокус кажется зрителям верхом акробатического искусства. Озадаченная публика в недоумении спрашивает себя: какая таинственная сила удерживает смельчака вниз головой? Недоверчиво настроенные готовы подозревать здесь ловкий обман, а между тем в трюке нет ничего сверхъестественного. Он всецело объясняется законами механики. Биллиардный шар, пущенный по этой дорожке, выполнил бы то же с не меньшим успехом. В школьных физических кабинетах имеются миниатюрные «чертовы петли».

Знаменитый исполнитель и изобретатель этого трюка, артист «Мефисто», для испытания прочности «чертовой петли» имел тяжелый шар, вес которого равнялся весу артиста вместо с велосипедом. Шар этот пускали по дорожке петли, и если он благополучно пробегал ее, то артист решался проделать петлю сам.

Читатель, конечно, догадывается, что причина странного явления – та же, которая объясняет общеизвестный опыт с вращающимся ведерком (стр. 55). Однако трюк удается не всегда; необходимо в точности рассчитать высоту, с которой велосипедист должен начать свое движение: иначе трюк окончится катастрофой.

Математика в цирке

Я знаю, что ряды «бездушных» формул отпугивают иных любителей физики. Но, отказываясь от знакомства с математической стороной явлений, такие недруги математики лишают себя удовольствия заранее предусматривать ход явления и определять его условия. В данном, например, случае две‑три формулы помогут нам в точности определить, при каких условиях возможно успешное выполнение столь удивительного трюка, как пробег в «чертовой петле».

Приступим же к расчетам.

Обозначим буквами те величины, с которыми придется вести расчеты:

буквой h обозначим высоту, с которой скатывается велосипедист;

буквой x обозначим ту часть высоты h, которая возвышается над верхней точкой «петли»; из рис. 42 очевидно, что x = h – АВ;

буквой r обозначим радиус круга петли;

буквой m – общую массу артиста вместе с велосипедом; вес их выразится тогда через mg, причем:

буквой g обозначено ускорение силы земной тяжести;

оно равно, как известно, 9,8 м/с за секунду;

буквой v обозначим скорость велосипеда в тот момент, когда он достигает самой верхней точки круга.

Все эти величины мы можем связать двумя уравнениями. Во‑первых, мы знаем из механики, что скорость, которую приобретает велосипед к моменту, когда, катясь по наклонной дорожке, он находится в C на уровне точки B (это положение изображено в нижней части на рис. 42), равна той, какую он имеет в верхней части петли, в точке B. Первая скорость выражается формулой[18]

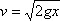
или v² = 2gx

Следовательно, и скорость и велосипедиста в точке B равна

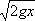
, т. е. v² = 2gx

Далее, для того чтобы велосипедист, достигнув высшей точки кругового пути, не упал вниз, нужно (см. стр. 55–56), чтобы развивающееся при этом центростремительное ускорение было больше, нежели ускорение тяжести, т. е. надо, чтобы

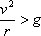
, или v²> gr

Но мы уже знаем, что v² = 2gx; следовательно, 2gx > gr или

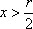
Итак, мы узнали, что для успешного выполнения этого головоломного фокуса необходимо устроить «чертову петлю» так, чтобы вершина наклонной части пути возвышалась над верхней точкой петли больше чем на ½ ее радиуса. Крутизна наклона роли не играет, – нужно только, чтобы пункт, с которого велосипедист начинает спускаться, возвышался над вершиной петли больше чем на ¼ ее поперечника. Если, например, петля имеет в поперечнике 16 м, то артист должен начать спуск не меньше чем с 20‑метровой высоты. Не выполни он этого условия, никакое искусство не поможет ему описать «чертову петлю»: достигнув ее верхней части, он неминуемо упадет.

Расчет этот не учитывает влияния силы трения в велосипеде: считается, что скорости в точке C и точке B одинаковы. Поэтому нельзя слишком удлинять путь и делать очень отлогий спуск. При отлогом спуске в результате действия трения скорость велосипеда по достижении точки B будет меньшей, чем в точке C.

Надо заметить, что при исполнении этого трюка велосипедист едет без цепи, предоставляя машину действию тяжести: ни ускорять, ни замедлять своего движения он не может, да и не должен. Все его искусство в том, чтобы держаться середины деревянной дорожки; при малейшем уклонении артист рискует съехать с дорожки и быть отброшенным в сторону. Скорость движения по кругу весьма велика: при круге с поперечником 16 м ездок совершает оборот в 3 секунды. Это соответствует скорости 60 км в час! Управлять велосипедом при такой скорости, конечно, мудрено; но этого и не надо; можно смело положиться на законы механики. «Сам по себе велосипедный трюк, – читаем мы в брошюре, составленной профессионалом, – при правильном расчете и прочной конструкции аппарата не опасен. Опасность трюка лежит в самом артисте. Если рука артиста дрогнет, если он будет взволнован, потеряет самообладание, если ему неожиданно сделается дурно, то можно ожидать всего».

На этом же законе покоится всем известная «мертвая петля» и другие фигуры высшего пилотажа. В «мертвой петле» первостепенную роль играет правильный «разгон» пилота по кривой и умелое управление самолетом.

Нехватка в весе

Какой‑то шутник объявил однажды, что знает способ без обмана обвешивать покупателей. Секрет состоит в том, чтобы покупать товары в странах экваториальных, а продавать – поближе к полюсам. Давно известно, что близ экватора вещи имеют меньший вес, нежели близ полюсов; 1 кг, перенесенный с экватора на полюс, прибавится в весе на 5 г. Надо пользоваться, однако, не обыкновенными весами, а пружинными, притом изготовленными (градуированными) на экваторе, иначе никакой выгоды не получится: товар станет тяжелее и на столько же тяжелее сделаются гири. Если купить тонну золота где‑нибудь в Перу, а сбыть ее, скажем, в Исландии, то можно, пожалуй, на этом кое‑что заработать, – при бесплатном провозе, разумеется.

Не думаю, чтобы подобная торговля могла кого‑нибудь обогатить, но по существу шутник прав: сила тяжести действительно увеличивается с удалением от экватора. Происходит это оттого, что тела на экваторе описывают при вращении Земли самые большие круги, а также и оттого, что земной шар как бы вздут у экватора.

Главная доля недостачи веса обусловлена вращением Земли; оно уменьшает вес тела близ экватора на 1/290 долю по сравнению с весом того же тела у полюсов.

Разница в весе при переносе тела с одной широты на другую для легких тел ничтожна. Но для предметов грузных она может достигнуть величины довольно солидной. Вы и не подозревали, например, что паровоз, весящий в Москве 60 тонн, по прибытии в Архангельск становится на 60 кг тяжелее, а по прибытии в Одессу – на столько же легче. В свое время с острова Шпицбергена ежегодно вывозили в более южные порты до 300 000 тонн угля. Если бы это количество было доставлено в какой‑нибудь экваториальный порт, то там обнаружена была бы недостача в 1200 тонн, будь груз перевешен при приемке на пружинных весах, вывезенных со Шпицбергена. Линкор, весивший в Архангельске 20 000 тонн, по прибытии в экваториальные воды становится легче тонн на 80; но это остается неощутимым, так как соответственно становятся легче и все другие тела, не исключая, конечно, и воды в океане[19].

Если бы земной шар вращался вокруг своей оси быстрее, чем теперь, например, если бы сутки длились не 24 часа, а, скажем, 4 часа, то разница в весе тел на экваторе и полюсах была бы заметна резче. При четырехчасовых сутках, например, гиря, весящая на полюсе 1 кг, весила бы на экваторе всего 875 г. Именно таковы приблизительно условия тяжести на Сатурне: близ полюсов этой планеты все тела на 1/6 тяжелее, чем на экваторе.

Так как центростремительное ускорение возрастает пропорционально квадрату скорости, то нетрудно вычислить, при какой скорости вращения оно на земном экваторе должно стать в 290 раз более, т. е. сравняться с силой притяжения. Это наступит при скорости, в 17 раз большей, нежели нынешняя (17×17 – почти 290). В таком состоянии тела перестанут оказывать давление на свои опоры. Другими словами, если бы Земля вращалась в 17 раз быстрее, вещи на экваторе совсем не имели бы веса! На Сатурне это наступило бы при скорости вращения, всего в 2,5 раза большей, чем нынешняя.

Глава четвертая