НАДЕЖНОСТЬ ОСНОВНОЙ СИСТЕМЫ
Основные системы (ОС) являются простейшими техническими системами, в которых отказ одного элемента приводит к отказу всей системы.
Работоспособность основной системы обеспечивается при условии, когда все n элементов системы находятся в работоспособном состоянии.
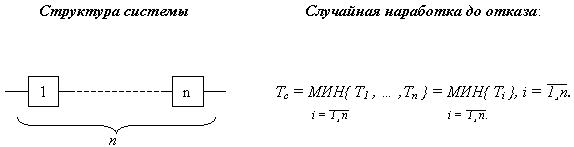
Поскольку события, заключающиеся в работоспособности элементов системы, являются независимыми, то
| вероятность безотказной работы (ВБР) ОС: | 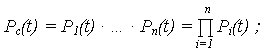
|
| вероятность отказа (ВО) ОС: | 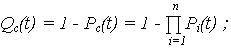
|
При идентичных элементах ОС P1(t) = … = Pn(t) = P(t):
| ВБР: | Pс(t) = P n(t) ; | ВО: | Qс(t) = 1 - P n(t) . |
Поскольку на участке нормальной эксплуатации наработку до отказа можно описать экспоненциальным распределением каждого элемента
Pi(t) = exp( - 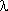 i · t),
i · t),
где 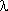 i = const, то
i = const, то
| ВБР ОС: | 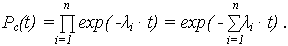
|
Используя уравнение связи показателей безотказности, выражающее ВБР любого объекта, в том числе и системы
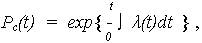
и полагая
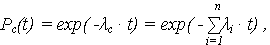
получаем, что интенсивность отказов (ИО) ОС равна сумме ИО элементов:
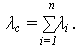
В общем случае, для любого распределения наработки ИО системы равна:
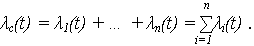
Для n идентичных элементов  1(t) = … =
1(t) = … =  n(t) =
n(t) = 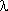 (t):
(t):
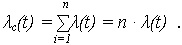
При экспоненциальном распределении наработки до отказа каждого из n элементов ОС Pi(t) = exp( - 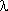 i · t), где
i · t), где 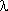 i = const показатели безотказности ОС определяются:
i = const показатели безотказности ОС определяются:
Неидентичные элементы
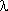 1 = … = 1 = … = 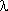 n = n = 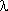
| Идентичные элементы
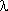 1 = … = 1 = … = 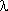 n = n = 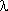
| |
| ВБР: | 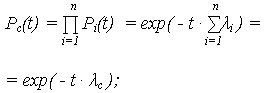
| 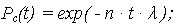
|
| ВО: | 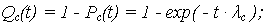
| 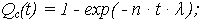
|
| ИО: | 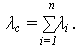
| 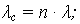
|
| МО наработки до отказа: | 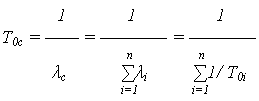
| 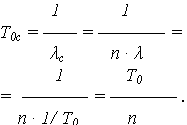
|
Выражения для МО наработки до отказа получены из формулы:
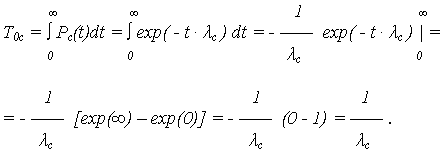
| ПРО: | fс(t) = - d Pс(t)/ dt = 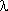 с exp( - t · с exp( - t · 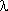 с ); с );
| fс(t) = n · 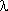 · exp( - n · t · · exp( - n · t · 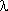 ) . ) .
|
Таким образом, при экспоненциальной наработке до отказа каждого из n элементов, распределение наработки до отказа ОС также подчиняется экспоненциальному распределению.
Для ОС надежность меньше надежности каждого из элементов. С увеличением числа элементов надежность ОС уменьшается.
Например, при n = 1000, Pi(t) = 0,99, Pс(t) < 10 - 4 и средняя наработка до отказа системы в 1000 раз меньше средней наработки каждого из элементов.
Дата добавления: 2015-12-08; просмотров: 698;
