Цель и структура технической диагностики
2. Постановка задач технической диагностики.
1.2. Основы технической диагностики.
а) Цель и структура технической диагностики.
Технической диагностикой называют науку о распознавании состояния технической системы.
Техническая диагностика изучает методы получения и оценки информации о состоянии системы (диагностической информации), модели, устанавливающие связь получаемой информации с состоянием системы (диагностические модели) и алгоритмы, в соответствие с которыми принимается решение о состоянии системы.
Цель технической диагностики – повышение показателей надежностью (в основном– ресурса) систем.
Наиболее важным показателем надежности является отсутствие отказов во время функционирования технической системы. Отказ авиационного двигателя в полете, судовых механизмов корабля, энергетических установок в работе под нагрузкой может привести к катастрофическим последствиям. Техническая диагностика благодаря раннему обнаружению дефектов и неисправностей позволяет устранить подобные отказы в процессе технического обслуживания, что повышает надежность, а также позволяет эксплуатировать технические системы ответственного назначения по их состоянию. (При эксплуатации по состоянию каждый экземпляр системы эксплуатируется до предельного состояния в соответствии с рекомендациями системы технической диагностики. Эксплуатация по техническому состоянию может принести существенную выгоду, эквивалентную 1/3 стоимости системы).
Основной задачей технической диагностики является распознание состояния технической системы в условиях ограниченной информации. Техническую диагностику называют также безразборной, подчеркивая тем самым важнейшее ее свойство определение состояния системы без разборки ее. В таких условиях получение информации затруднено и заключение о состоянии системы делается на основе статистических методов.
Но техническая диагностика решает не только задачу по распознаванию состояния системы, но и занимается разработкой методов поиска неисправностей.
В связи с этим в диагностике выделяют два взаимосвязанных направления.
Первое из них, базируясь на определенной, полученной от исследуемой системы информации, определяет состояние системы: работоспособна – неработоспособна. Теоретическим фундаментом .для решения задач этого направления служит теория распознавания образов , являющаяся одним из разделов технической, кибернетики – науки об управлении техническими системами.
Второе направление базируется на теории контролеспособности. Контролеспособностью называется свойство системы обеспечивать достоверную оценку ее технического состояния и раннее обнаружение неисправностей и отказов. Контролеспособность обеспечивается конструкцией системы и принятой системой технической диагностики.
Структура технической надежности в соответствии с выделенными направлениями имеет вид, представленный на рис. 1.7.

Рис. 1.7
Алгоритмы, правила решения и модели – важнейшие компоненты теории распознавания. Алгоритмы распознавания, определяющие ход процесса диагностирования, основываются на диагностических моделях, устанавливающих (как уже отмечалось) связь между состояниями технической системы и их отображениями в пространстве диагностических сигналов. При этом существенным является выбор правила принятия решения об отнесении системы к тому или иному классу (исправных или неисправных). Решение названной задачи всегда связано с риском ложной тревоги (принять исправную, систему за неисправную) или пропуска цели (принять неисправную систему за исправную). Для принятия обоснованного решения в этом случае привлекаются методы теории статистических решений.
В теории контролеспособности можно, выделить три основных аспекта:
1 изучение методов, и средств получения диагностической информации;
2 контроль состояния системы, предусматривающий использование диагностической информации, и формирование управляющих воздействий на систему;
3 поиск неисправностей, обеспечивающий наибольшую эффективность этого процесса за счет разработки соответствующих алгоритмов поиска и диагностических тестов.
б) Постановка задач технической диагностики.
С целью большей наглядности постановку задач осуществим с использованием конкретного примера.
Пусть требуется определить состояние шлицевых соединений коробки передач в условиях эксплуатации. При большом износе шлицев появляются перекосы и усталостные разрушения. Непосредственный осмотр, шлицев невозможен так как требует разборки коробки, т.е. прекращение эксплуатации. Неисправность шлицевых соединений проявляет себя через спектр колебаний корпуса коробки, акустические колебания, содержание частиц металла в масле и другие параметры.
Задача технической диагностики состоит в определении степени износа шлицев (глубины разрушенного поверхностного слоя) по данным измерения ряда косвенных параметров. Как указывалась, одной из основных особенностей технической диагностики, является распознавание в условиях ограниченной информации, когда требуется руководствоваться определенными приемами и правилами для принятия обоснованного решения.
Распознавание состояния системы – это отнесение состояния системы и одному из возможных классов (диагнозов). Число диагнозов зависит от особенностей задачи и целей исследования. Наиболее часто требуется провести выбор из двух диагнозов: "исправное состояние" – "неисправное состояние". В других случаях необходимо более подробно охарактеризовать неисправное состояние. В большинстве задач технической диагностики диапазоны устанавливаются заранее и задачу распознавания называют задачей классификации.
Так как: техническая диагностика связана с обработкой большого объема информации, те принятие решений (распознавание) осуществляется как правило с использованием ЭВМ.
Совокупность последовательных действий в процессе распознавания называется алгоритмом распознавания. Важнейшей частью процесса распознавания является выбор параметров, описывающих состояние системы. Они должны содержать такое количество, информации, чтобы при, выбранном числе диагнозов процесс распознавания мог быть осуществлен.
Теперь от словесной (вербальной) постановки задачи распознавания, включающий выбор параметров, разработку моделей, алгоритмов и правил принятия решения, перейдем к математической постановке.
В задачах диагностики состояние системы описывают с помощью комплекса признаков:
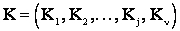 ,
,
где 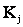 – признак, имеющий j разрядов.
– признак, имеющий j разрядов.
Пусть, например, .признак характеризует температуру газа на выходе двигателя и является 3–х разрядным, .т.е. температура рассматривается как пониженная, нормальная и повышенная. Каждый разряд признака 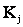 обозначается
обозначается 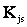 , например, повышается температура
, например, повышается температура 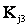 . Фактически наблюдаемое состояние соответствует определенному значению признака, что отмечают верхним индексом (*). Так, при повышенной температуре реализация признака
. Фактически наблюдаемое состояние соответствует определенному значению признака, что отмечают верхним индексом (*). Так, при повышенной температуре реализация признака 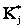 будет
будет 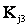 .
.
В общем случае каждый экземпляр системы соответствует некоторой реализации комплекса признаков
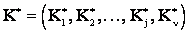
При решении ряда задач систему удобно характеризовать не дискретными признаками 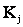 , а непрерывными параметрами
, а непрерывными параметрами 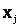 , образующими n-мерный вектор и точку в n-мерном пространстве:
, образующими n-мерный вектор и точку в n-мерном пространстве:
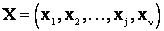 .
.
При непрерывном описании требуется значительно больший объем информации, но точность описания возрастает. Однако, если известны статистические законы распределения параметра, то необходимый объем информации сокращается. Принципиальных отличий при описании системы с помощью .признаков или параметров нет.
К задаче распределения существуют два подхода: .вероятностный и детерминированный.
Постановка задачи распознавания при вероятностном подходе
Имеется система, которая находится в одном из n случайных состояний 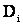 (все возможные состояния системы
(все возможные состояния системы 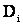 , т.е. диагнозы, известны). Известна совокупность признаков или параметров, каждый, из которых с определенной вероятностью характеризует состояние системы. Для решения задачи требуется построить решающие правило, с помощью которого имеющаяся совокупность признаков была бы отнесена к одному из возможных состояний (диагнозов). Необходимо также оценить достоверность принятого решения и степень риска ошибочного решения.
, т.е. диагнозы, известны). Известна совокупность признаков или параметров, каждый, из которых с определенной вероятностью характеризует состояние системы. Для решения задачи требуется построить решающие правило, с помощью которого имеющаяся совокупность признаков была бы отнесена к одному из возможных состояний (диагнозов). Необходимо также оценить достоверность принятого решения и степень риска ошибочного решения.
Постановка задачи распознавания при детерминированном подходе
В этом случае задачу удобно формулировать с использованием геометрических образов. Если система характеризуется n-мерным вектором Х, то любое состояние системы представляет точку в n-мерном пространстве параметров. Предполагается, что диагноз 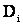 соответствует некоторой области рассматриваемого пространства параметров. Требуется найти решающее правило, в соответствии с которым предъявленный вектор X (диагностируемое состояние системы) будет отнесен к определенной области диагноза. Таким образом, задача сводится к разделению пространства параметров на области диагнозов.
соответствует некоторой области рассматриваемого пространства параметров. Требуется найти решающее правило, в соответствии с которым предъявленный вектор X (диагностируемое состояние системы) будет отнесен к определенной области диагноза. Таким образом, задача сводится к разделению пространства параметров на области диагнозов.
При детерминированном подходе области диагнозов обычно считаются непересекающимися.
Оба рассмотренных подхода не имеют принципиальных различий. Вероятностный является более общим, но требует значительно большего объема предварительной информации. Детерминированный более кратко описывает существенные стороны процесса распознавания, меньше зависит от избыточной информации.
Дата добавления: 2015-12-08; просмотров: 1060;
