ЗАРОДЖЕННЯ ТА РОЗВИТОК ФІЗИКИ ЯК НАУКИ 6 страница

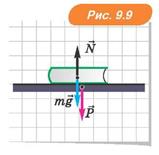
На книжку діють дві сили: сила тяжіння 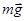і сила пруж­ності 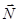з боку ліфта. А з боку книжки на ліфт діє сила пруж­ності 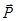— вага книжки (рис. 9.9).

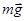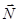Але тепер сили і не врівноважують одна одну, бо 'їх рівнодійна 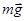+ 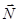надає книжці прискорення 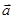. Згідно з дру­гим законом Ньютона 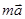= 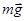+ 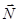, а відповідно до третього закону Ньютона 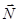= - 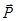. Тому 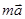= 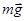- 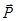. Звідси отримуємо, що вага тіла, яке рухається з прискоренням, виражається формулою =

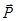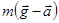
Зверніть увагу: вага тіла залежить тільки від прискорення і не залежить від швидкості.

У якому випадку вага тіла біль­ша за силу тяжіння, а в якому — менша? Якщо прискорення тіла напрямлене вгору, 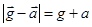, тому Р =m(g + a)> mg. Якщо ж прискорення напрямлене вниз (і не більше за модулем, ніж прискорення вільного падіння), то 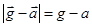, а отже, Р =m(g -а) < mg.

РОЗВ'ЯЖІМО ЗАДАЧУ

Вантаж масою 100 кг піднімають з напрямленим угору

прискоренням, що дорівнює за модулем 2м/с². Якою є

сила натягу троса, яким піднімають вантаж?

Розв'язання. Сила натягу тросу — це вага вантажу. При­скорення вантажу напрямлене вгору, тому в цьому випадку P=m(g + a) = 100·(10 + 2) = 1200 (Н).

Відповідь: 1200 Н.

Зверніть увагу: якщо прискорення вантажу напрямлене вгору, то сила натягу троса більша від сили тяжіння, що діє на вантаж. Згідно з третім законом Ньютона з такою самою за модулем силою вантаж розтягує трос. А сила, з якою вантаж розтягує трос, і є вагою вантажу. Отже, якщо вантаж рухається з прискоренням, напрямленим угору, то вага вантажу

P=m(g + a)

Якщо ж прискорення тіла напрямлене вниз (але не біль­ше за модулем, ніж прискорення вільного падіння), то вага тіла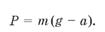

P=m(g - a)

З цієї формули випливає, зокрема, що коли тіло рухається з прискоренням, рівним прискоренню вільного падіння, то його вага дорівнює нулю. Розглянемо цей випадок докладніше.

НЕВАГОМІСТЬ

Коли тіло вільно падає, воно не тисне на опору і не роз­тягує підвіс. А це означає, що вага тіла, яке вільно падає, дорівнює нулю.

Стан, у якому вага тіла дорівнює нулю, називають неваго­містю.

Зверніть увагу: у невагомості вага тіла дорівнює нулю, але сила тяжіння, як і раніше, дорівнює .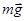

У невагомості перебувають усі тіла, на які діє тіль­ки сила тяжіння (наприклад, космонавти під час польоту з вимкненими двигунами — у цьому випадку космічний ко­рабель і всі тіла, що є в ньому, рухаються тільки під дією сили тяжіння, тобто перебувають у невагомості).

На короткий час ви можете стати невагомим, просто під­стрибнувши. З того моменту, коли ваші ноги відірвуться від підлоги, і до того моменту, коли вони торкнуться підлоги знову, ви перебуватимете в невагомості: адже при цьому ви не тиснете на опору і не розтягуєте підвіс. Яскраві враження від відчуття невагомості можна дістати, стрибаючи на батуті¹ (рис. 9.10). Але перебуваючи в невагомості протягом кількох секунд, не можна відчути невагомість так, як її відчувають космонавти, які перебувають у невагомості місяцами.

5. ЧИ ОЧЕВИДНИЙ ТРЕТІЙ ЗАКОН НЬЮТОНА?

Незважаючи на простоту формулювання третій закон Ньютона так само не очевидний, як і два перших.

Річ у тім, що рівні за модулем сили, з якими взаємодіють два тіла, далеко не завжди виявляють себе однаково поміт­но. Розглянемо приклади.

Падіння каменя. Коли камінь падає, збільшення його швидкості внаслідок дії сили притягання Землі добре поміт­не: швидкість каменя за кожну секунду збільшується при­близно на 10 м/с.

На Землю з боку каменя діє така сама за модулем сила притягання. Але внаслідок того, що маса Землі в багато разів більша від маси каменя, помітити зумовлене дією цієї сили прискорення Землі неможливо.

Удар по м'ячу. Коли футболіст б'є по м'ячу, м'яч різко змі­нює швидкість, але швидкість самого футболіста при цьому майже не змінюється. Це пояснюється не тільки тим, що маса футболіста набагато більша від маси м'яча. Важливо ще й те, що на футболіста з боку Землі діє велика сила тертя: саме для того, щоб збільшити її, футболісти і надягають бутси із ши­пами. Якби футболіст сильно бив по м'ячу, стоячи на льоду в туфлях, він під час удару теж набув би помітної швидкості.

«Неочевидність» простих на перший погляд законів при­роди (у тому числі трьох законів Ньютона) має глибокий сенс. Щоб у складних та взаємозалежних явищах природи поміти­ти просту закономірність, потрібна проникливість справжньо­го вченого.

Вивчаючи фізику, ви й сьогодні стикаєтеся з тією ж «ди­вовижністю» і «неочевидністю» законів природи, що довгий час «заважала» людям побачити ці закономірності й відкри­ти закони природи.

6. МЕЖІ ЗАСТОСОВНОСТІ ЗАКОНІВ НЬЮТОНА

Усі фізичні закони й теорії є наближенням до дійсності, оскільки у будь-якій теорії використовується модель явищ і процесів. Тому як закони, так і теорії мають певні межі застосовності.

Мають межі застосовності й закони Ньютона. Наприклад, другий закон Ньютона, як ви знаєте, виконується тільки в інерціальних системах відліку.

Засновану на законах Ньютона теорію називають кла­сичною механікою. Як показує досвід, класична механіка справедлива для руху тіл зі швидкостями, набагато мен­шими від швидкості світла. Якщо ж швидкості тіл порів­нянні зі швидкістю світла (з такими швидкостями руха­ються відносно Землі, наприклад, віддалені галактики та елементарні частинки в прискорювачах), висновки класич­ної механіки суперечать дослідам і спостереженням. Для тіл, що рухаються зі швидкостями, порівнянними зі швид­кістю світла, справедлива спеціальна теорія відносності, створена видатним фізиком Альбертом Ейнштейном¹ на

початку 20-го століття. Основні положення спеціальної те­орії відносності ми розглянемо в Розділі 3. Релятивіст­ська механіка.

Класичну механіку не можна застосовувати також для опису руху та взаємодії частинок дуже малої маси — на­приклад, електронів. Тому в межах класичної механіки не можна зрозуміти, скажімо, особливості будови атома. Для розуміння атомних явищ на початку 20-го століття зусилля­ми декількох учених різних країн було створено квантову механіку. Основні її положення розглядатимуться в курсі фізики 11-го класу.

^[1] Проекції вектора в курсі геометрії називають координатами вектора.

^[2] Якщо сили, що діють на тіло, урівноважують одна одну, кажуть також, що дії цих сил скомпенсовані.

^[3] Через те й було вибрано таку одиницю маси: її легко відтворити з точністю, достатньою для багатьох випадків.