ЗАРОДЖЕННЯ ТА РОЗВИТОК ФІЗИКИ ЯК НАУКИ 2 страница

|
Розкрутимо диск, піднесемо до нього рейку (не торкаючись диска) і проведемо уздовж рейки грудочкою крейди, щоб крейда залишила слід на диску. У системі відліку, пов'язаній із Землею, траєкторія грудочки крейди прямолінійна — крейда рухається вздовж рейки. Однак на диску крейда викреслює спіраль, що показує траєкторію руху тієї ж грудочки крейди в системі відліку, пов'язаній з диском.
5. ВЕКТОРНІ ВЕЛИЧИНИ У ФІЗИЦІ
У фізиці використовують багато векторних величин. Такими величинами є, наприклад, переміщення, швидкість, сила. Розглядаючи багато задач, треба вміти виконувати різні дії з векторними величинами. Розглянемо тут додавання векторних величин на прикладі додавання переміщень.
Нехай літак перелетів з міста М до міста Н, а звідти — до міста К. На рисунку 1.12, а вектором 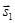 позначено переміщення літака з М у Н, а вектором
позначено переміщення літака з М у Н, а вектором 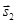 — переміщення літака
— переміщення літака
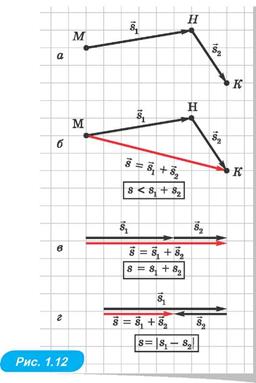
з Н у К. Результатом двох переміщень є переміщення s — це вектор, що з'єднує М і К.
Ми виконали зараз додавання векторів  за «правилом трикутника».
за «правилом трикутника».
Щоб за цим правилом знайти суму двох векторів, треба початок другого вектора з'єднати з кінцем першого вектора (рис. 1.12, а). Тоді сумою цих двох векторів є вектор, початок якого збігається з початком першого вектора, а кінець — з кінцем другого вектора (рис. 1.12, б).
За допомогою «правила трикутника» можна додавати також вектори, напрямлені вздовж однієї прямої (рис. 1.12, в, г). Щоправда, у цьому випадку справжній трикутник не виходить, бо всі вектори лежать на одній прямій. Зверніть увагу: у цьому випадку рівність 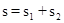 має місце тільки тоді, коли вектори-доданки напрямлені однаково (рис. 1.12, в). Якщо ж вектори-доданки напрямлені протилежно, то
має місце тільки тоді, коли вектори-доданки напрямлені однаково (рис. 1.12, в). Якщо ж вектори-доданки напрямлені протилежно, то 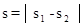 (рис. 1.12, г).
(рис. 1.12, г).
ПРОЕКЦІЇ ВЕКТОРНОЇ ВЕЛИЧИНИ НА ОСІ КООРДИНАТ
При розв'язуванні задач зазвичай складають рівняння, що зв'язують фізичні величини, а потім розв'язують ці рівняння. Якщо величини векторні, доводиться «стежити» не тільки за модулем кожної такої величини, але й за її напрямом. Розв'язання задач значно спрощується завдяки тому, що одну векторну величину можна задати за допомогою кількох скалярних величин у такий спосіб.
|
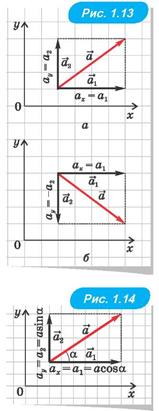
Будь-яку векторну величину можна представити у вигляді суми трьох векторних величин, напрямлених уздовж осей координат. Ці векторні величини називають її складовими. А кожну складову векторної величини можна охарактеризувати числом: модуль цього числа дорівнює модулю складової, а знак числа визначається напрямом складової. Якщо вона напрямлена в додатному напрямі осі координат, то це число додатне, а якщо у від'ємному — то від'ємне. Це число називають проекцією даної векторної величини на відповідну координатну вісь[1].
Проекції векторної величини а на осі координат x, y, z позначають ax, ay і az. Вони мають ті самі одиниці, що й модуль величини 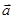 . Наприклад, одиниці проекції переміщення — метри, а проекції швидкості — метри за секунду. На рис. 1.13 показано, як знаходити проекції векторної величини, заданої на площині. На рис. 1.13, а обидві проекції вектора
. Наприклад, одиниці проекції переміщення — метри, а проекції швидкості — метри за секунду. На рис. 1.13 показано, як знаходити проекції векторної величини, заданої на площині. На рис. 1.13, а обидві проекції вектора 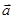 додатні, а на рис. 1.13, б проекція вектора
додатні, а на рис. 1.13, б проекція вектора 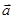 на вісь x додатна, а на вісь y — від'ємна.
на вісь x додатна, а на вісь y — від'ємна.
Ще раз звертаємо увагу на те, що знак проекції може бути як позитивним, так і негативним.
Виразимо проекції векторної величини 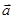 , заданої на площині, через її модуль a і кут α між напрямом
, заданої на площині, через її модуль a і кут α між напрямом 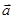 і віссю x.
і віссю x.
Як видно з рис. 1.14, ax = a cos α, ay = a sin α. Оскільки складові век-
торної величини і сама векторна величина утворюють прямокутний трикутник, модуль векторної величини виражається через її проекції за допомогою  формули
формули 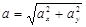
При додаванні векторних величин їхні проекції додаються.
|
ЯК ПОВ'ЯЗАНІ ПРОЕКЦІЇ ПЕРЕМІЩЕННЯ ТІЛА З ЙОГО КООРДИНАТАМИ?
Для наочності обмежимося  рухом на площині.
рухом на площині.
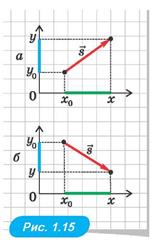
Нехай тіло з точки з координатами x0, y0 перемістилося в точку з координатами x, y (рис. 1.15). Тоді переміщення 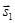 — це вектор, проведений із точки з координатами x0, y0 у точку з координатами x, y. Отже, sx = x - x0, sy = y - y0. Таким чином,
— це вектор, проведений із точки з координатами x0, y0 у точку з координатами x, y. Отже, sx = x - x0, sy = y - y0. Таким чином,
Х = xo + sx, у = yo + sy.
Зверніть увагу: у цих формулах стоїть знак «плюс» незалежно від того, у якому напрямі рухалося тіло — у додатному напрямі осі (рис. 1.15, а) чи у від'ємному (на рис. 1.15, б тіло рухається у від'ємному напрямі осі у).
ПРО ЩО МИ ДІЗНАЛИСЯ
• Механічним рухом називають зміну з часом положення тіла відносно інших тіл.
• Основне завдання механіки полягає в тому, щоб визначити положення тіла в будь-який момент часу. Для розв'язання основного завдання механіки треба знати початкове положення тіла, його швидкість у початковий момент часу й те, як швидкість змінюється з часом.
• Тіло, розмірами якого в даній задачі можна знехтувати, називають матеріальною точкою. Тіло можна вважати матеріальною точкою, якщо розміри тіла малі порівняно з відстанню, пройденою тілом, а також у разі, коли тіло рухається поступально.
• Тіло, відносно якого розглядають рух усіх тіл у даній задачі, називають тілом відліку.
• Тіло відліку та пов'язані з ним система координат і годинник утворюють систему відліку.
• Лінію в просторі, по якій рухається тіло, називають траєкторією руху тіла.
• Довжину траєкторії називають шляхом, пройденим тілом.
• Переміщення тіла — напрямлений відрізок, проведений з початкового положення тіла в його положення в даний момент часу.
• Форма траєкторії, шлях та переміщення тіла залежать від вибору системи відліку.
ЗАПИТАННЯ ТА ЗАВДАННЯ
Перший рівень
1. Наведіть приклади задач, коли ваше власне тіло можна вважати матеріальною точкою, а коли — ні.
2. Наведіть приклади задач, у яких спортсмена можна розглядати як матеріальну точку і в яких не можна.
3. Навіщо потрібна система відліку? З чого вона складається?
4. Що приймають за тіло відліку, коли говорять: а) автомобіль їде зі швидкістю 100 км/год; б) Земля рухається по своїй орбіті зі швидкістю 30 км/с?
5. Чи може траєкторія руху перетинати себе? Наведіть приклади, що підтверджують вашу відповідь.
6. Чим відрізняється шлях від переміщення? Чи може шлях під час руху тіла зменшуватися?
Другий рівень
7. Як рухається тіло, якщо модуль переміщення дорівнює шляху, пройденому тілом?
8. Яка траєкторія руху тіла, якщо його переміщення дорівнює нулю, а шлях нулю не дорівнює?
9. Хлопчик їде на велосипеді по прямолінійній ділянці горизонтального шляху. Намалюйте в зошиті траєкторію руху сідла велосипеда відносно шляху; педалей велосипеда.
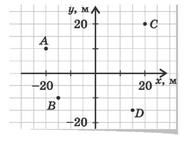
10. На рисунку показано послідовні положення A, B, C, D через рівні проміжки часу бджоли, яка літає лугом. Перенесіть рисунок у зошит і накресліть вектори переміщень бджоли за кожний з цих проміжків.
§ 2. ПРЯМОЛІНІЙНИЙ РІВНОМІРНИЙ
РУХ
1. Швидкість прямолінійного рівномірного руху
2. Графіки прямолінійного рівномірного руху
3. Середня швидкість
1. ШВИДКІСТЬ ПРЯМОЛІНІЙНОГО РІВНОМІРНОГО РУХУ
Найпростіший вид руху — прямолінійний рівномірний рух.
Прямолінійним рівномірним рухом називають рух, під час якого тіло за будь-які рівні проміжки часу здійснює однакові переміщення.
Прямолінійним рівномірним рухом є, наприклад, рух автомобіля по прямому шосе, коли спідометр «застигає» на одному показанні, скажімо «60 км/год».
Швидкість прямолінійного рівномірного руху дорівнює відношенню переміщення тіла до проміжку часу, за який відбулося це переміщення:
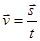
З цієї формули випливає, що
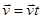
Зручно направити вісь x уздовж прямої, по якій рухається тіло, тоді 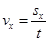
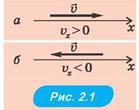
|
Проекція швидкості vx може бути як додатною (рис. 2.1, а), так і від'ємною (рис. 2.1, б) — залежно від того, у якому напрямі осі x рухається тіло.
Формули залежності від часу проекції переміщення sx і координати x мають вигляд:
Sx = vxt , х = х0 + vxt
Одиниця швидкості в SI — 1 м/с. Це швидкість неспішної прогулянки. Ідучи з такою швидкістю, людина проходить за одну годину 3600 м, тобто її швидкість дорівнює 3,6 км/год. Швидкість автомобілів і потягів задають зазвичай у кілометрах за годину.
Швидкість ракет і штучних супутників Землі задають у кілометрах за секунду (км/с).
Як ми побачимо в § 10. Закон всесвітнього тяжіння, швидкість руху штучного супутника Землі навколоземною орбітою становить близько 8 км/с.
2. ГРАФІКИ ПРЯМОЛІНІЙНОГО РІВНОМІРНОГО РУХУ
Наочне уявлення про рух тіла дають графіки залежності від часу швидкості, переміщення, координати і шляху. Розглянемо, як будують ці графіки, на конкретному прикладі.
РОЗВ'ЯЖІМО ЗАДАЧУ
По прямій дорозі їдуть велосипедист і автомобіль. Велосипедист їде в одному напрямі зі швидкістю 25 км/год, автомобіль — у протилежному напрямі зі швидкістю 50 км/год. У початковий момент велосипедист перебував у точці з координатою x = 25 км, автомобіль — у точці з координатою x = 100 км. Побудуємо графіки залежності від часу проекції швидкості, переміщення, координати та шляху.
Розв'язання. Направимо вісь x у напрямі швидкості велосипедиста.
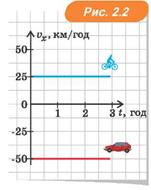
|
Графіки залежності проекції швидкості від часу. Оскільки тіла рухаються з постійною швидкістю, графік функції vx(t) — пряма, паралельна осі t. Для велосипедиста vx > 0, тому графік проходить вище осі t, а для автомобіля vx < 0, тому графік проходить нижче осі t. Ці графіки наведено на рис. 2.2.
Графік залежності проекції швидкості від часу для прямолінійного рівномірного руху може здатися не надто цікавим. Однак він має важливу властивість, яка невдовзі нам допоможе. Для зручності розглянемо випадок, коли проекція швидкості є додатною. Тоді
площа фігури, обмеженої графіком vx (t) і віссю t, чисельно дорівнює проекції переміщення.
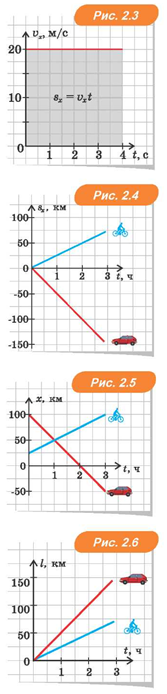 |
Щоб переконатися в цьому, розглянемо фігуру, розташовану під графіком проекції швидкості (її виділено кольором на рис. 2.3).
Ця фігура — прямокутник. Його площа дорівнює добутку висоти vx на основу t, тобто дорівнює vxt. А це чисельно дорівнює переміщенню за умови прямолінійного рівномірного руху.
Графік залежності проекції переміщення від часу. З формули sx (t) = vxt випливає, що графіком sx(t) є пряма, що проходить через початок координат (рис. 2.4). Якщо vx > 0, то sx збільшується з часом (саме так для велосипедиста), а якщо vx < 0, то sx зменшується з часом (саме так для автомобіля).
Зверніть увагу на те, що нахил графіка sx (t) тим більший, чим більший модуль швидкості.
Графік залежності координати від часу. Графік x (t) = x0 + sx(t) відрізняється від графіка sx (t) тільки зсувом на x0 по осі ординат (рис. 2.5). Точка перетину двох графіків відповідає моменту, коли координати тіл збігаються, отже, ця точка графіка визначає момент часу і координату зустрічі двох тіл.
По наведених графіках видно, що велосипедист і автомобіль протягом першої години рухалися назустріч один одному, а потім — віддалялися один від одного.
Графік шляху. Зверніть увагу: хоча велосипедист і автомобіль рухаються в протилежних напрямах, в обох випадках пройдений кожним з них шлях зростає з часом (рис. 2.6).
3. СЕРЕДНЯ ШВИДКІСТЬ
Прямолінійний рівномірний рух зустрічається досить рідко. Значно частіше ми спостерігаємо приклади нерівномірного руху.
Нерівномірним рухом називають такий рух, під час якого тіло проходить за рівні проміжки часу різні шляхи.
Прикладами нерівномірного руху можуть служити падіння яблука з гілки дерева, розгін і гальмування автомобіля.
Для опису нерівномірного руху часто використовують середню швидкість.
Середньою швидкістю нерівномірного руху 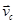 за даний проміжок часу t називають фізичну величину, що дорівнює відношенню переміщення s до проміжку часу, за який це переміщення відбулося:
за даний проміжок часу t називають фізичну величину, що дорівнює відношенню переміщення s до проміжку часу, за який це переміщення відбулося:
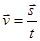
Слова «за даний проміжок часу» вказують на те, що за умови нерівномірного руху середня швидкість тіла за різні проміжки часу може бути різною.
Наприклад, коли автомобіль розганяється, то його середня швидкість за першу секунду може дорівнювати 5 м/с, а за
другу секунду — вже 10 м/с. А для автобуса, що гальмує,
навпаки, середня швидкість за кожну наступну секунду менша, ніж за попередню.
ПРО ЩО МИ ДІЗНАЛИСЯ
• Прямолінійним рівномірним рухом називають такий рух тіла, під час якого воно за будь-які рівні проміжки часу здійснює рівні переміщення.
• Швидкість прямолінійного рівномірного руху дорівнює відношенню переміщення s тіла до проміжку часу t, за який здійснено це переміщення: 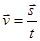 . Швидкість — величина векторна.
. Швидкість — величина векторна.
• Формули залежності від часу переміщення, проекції переміщення та координати мають вигляд: 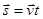 , sx = vxt, x = x0 + vxt.
, sx = vxt, x = x0 + vxt.
• Графіком залежності проекції переміщення від часу за умови прямолінійного рівномірного руху є відрізок прямої, один кінець якого збігається з початком координат. Чим більша швидкість тіла, тим більший кут між графіком залежності проекції переміщення від часу та віссю часу.
• Нерівномірним рухом називають такий рух, під час якого тіло проходить за рівні проміжки часу різні шляхи.
Середньою швидкістю нерівномірного руху за даний проміжок часу t називають фізичну величину, що дорівнює відношенню переміщення до проміжку часу, за який це переміщення відбулося:
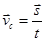
ЗАПИТАННЯ ТА ЗАВДАННЯ
Перший рівень
1. Наведіть приклади прямолінійного рівномірного руху.
2. Автомобіль рухається рівномірно по прямому шосе. З якою швидкістю їде автомобіль, якщо кожної хвилини він проїжджає повз кілометровий стовп?
3. Хороший спортсмен пробігає стометрівку за 10 с. Яка його швидкість у метрах за секунду та в кілометрах за годину?
4. Автомобіль їде зі швидкістю 20 м/с. Яка його швидкість у кілометрах
за годину?
5.Побудуйте на одному рисунку графіки залежності шляху від часу для двох автомобілів — синього і червоного. Синій рухається зі швидкістю 60 км/год, а червоний — зі швидкістю 100 км/год. Для якого автомобіля кут між графіком та віссю часу більший?
6. Що таке нерівномірний рух? Наведіть декілька прикладів такого
руху.
7. Що таке середня швидкість? Як пов'язаний модуль середньої швидкості зі шляхом під час прямолінійного руху в одному напрямі?
8. Автомобіль за 1 год проїхав 60 км, потім 1 год стояв, а потім ще за 1 год проїхав 90 км. Автомобіль весь час рухався прямолінійним шосе в одному напрямі. Яка середня швидкість автомобіля?
Другий рівень
9. Який вигляд має графік залежності шляху від часу за умови прямолінійного рівномірного руху? Намалюйте такі графіки для двох автомобілів, якщо швидкість першого автомобіля удвічі більша за швидкість
другого.
|
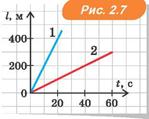
10. На рис. 2.7 наведено графіки залежності шляху від часу для двох тіл, що рухаються прямолінійно. Знайдіть швидкість руху кожного з цих тіл. У скільки разів швидкість першого тіла більша за швидкість другого?
11. Який вигляд має графік залежності модуля швидкості від часу за умови прямолінійного рівномірного руху? Як можна знайти пройдений шлях за допомогою графіка швидкості?
12. Залежність координати тіла від часу в одиницях SI має вигляд x = -15 + 2,5t. З якою швидкістю рухається тіло та в якому напрямі відносно вісі х? Через який час координата тіла дорівнюватиме 15 м?
13.Пасажир проїхав половину часу на автомобілі зі швидкістю 100 км/год, а половину часу — потягом зі швидкістю 60 км/год. Чому дорівнює його
середня швидкість за весь час руху? Автомобіль та поїзд весь час рухалися по прямій в одному напрямі.
14. Пасажир проїхав першу половину шляху на автомобілі зі швидкістю
100 км/год, а другу половину шляху — потягом зі швидкістю 60 км/год
Чому дорівнює його середня швидкість за весь час руху? Автомобіль весь час рухався прямолінійним шосе в одному напрямі. Чому відповідь цієї задачі відрізняється від відповіді попередньої?
15. Складіть задачу за темою «Прямолінійний рівномірний рух», відповіддю якої було б «Не наздожене».
§ 3. ПРЯМОЛІНІЙНИЙ
РІВНОПРИСКОРЕНИЙ РУХ
1. Миттєва швидкість
2. Прискорення
3. Прямолінійний рівноприскорений рух
4. Вільне падіння
1. МИТТЄВА ШВИДКІСТЬ
Якщо швидкість тіла змінюється з часом, для опису руху треба знати, чому дорівнює швидкість тіла в даний момент часу (або в даній точці траєкторії). Цю швидкість називають миттєвою швидкістю.
Наочне уявлення про миттєву швидкість дає прилад для вимірювання швидкості автомобіля — спідометр (рис. 3.1).

|
Можна сказати, що миттєва швидкість — це середня швидкість за дуже малий проміжок часу. Під час руху зі змінною швидкістю середня швидкість, вимірювана за різні проміжки часу, буде різною. Проте якщо при вимірюванні середньої швидкості брати щораз менші проміжки часу, значення середньої швидкості наближатиметься до деякого певного значення. Це і є миттєва швидкість у даний момент часу. Надалі, говорячи про швидкість тіла, ми матимемо на увазі його миттєву швидкість.
Поняття миттєвої швидкості добре ілюструє такий приклад зі знаменитих «Фейнманівських лекцій з фізики» (рис. 3.2).
Поліцейський зупиняє машину, і між ним та жінкою за кермом відбувається така розмова.
— Ви порушили правила дорожнього руху: їхали зі швидкістю 90 кілометрів за годину.
— Я всього 7 хвилин тому виїхала з дому, як же я могла проїхати 90 кілометрів за годину?
— Але якби ви продовжували так їхати, то ви проїхали б за годину 90 кілометрів.

— А я й не збиралася так їхати аж годину! Я збиралася проїхати ще один квартал і зупинитися.
Як би ви на місці поліцейського довели, що правила дорожнього руху все-таки було порушено?
2. ПРИСКОРЕННЯ
Якщо швидкість тіла під час руху змінюється, виникає питання: якою є «швидкість зміни швидкості»? Ця величина, яку називають прискоренням, відіграє дуже важливу роль у всій механіці: незабаром ми побачимо, що прискорення тіла визначається діючими на це тіло силами.
Нехай швидкість тіла в момент часу t1 дорівнювала 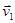 а в момент часу t2 стала рівною
а в момент часу t2 стала рівною 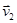 . Позначимо зміну швидкості
. Позначимо зміну швидкості 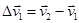 а проміжок часу
а проміжок часу 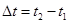
Прискоренням називають1 відношення зміни швидкості тіла до проміжку часу, за який ця зміна відбулася:
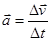
Як випливає з визначення, прискорення — величина векторна. Напрям при скорення збігається з напрямом вектора зміни швидкості Av.
Приклади:
1. Коли автомобіль розганяється, його прискорення напрямлене в той же бік, що і швидкість.
2. Коли автомобіль гальмує, його прискорення напрямлене протилежно швидкості.
1 Це визначення середнього прискорення за час At. Миттєвим прискоренням називають середнє прискорення за дуже малий проміжок часу.
Одиниця прискорення в SI: 1 м/с2. Якщо тіло рухається в певному напрямі з прискоренням 1 м/с2, його швидкість змінюється щосекунди на 1 м/с.
Термін «прискорення» використовують у фізиці, коли мова йде про будь-яку зміну швидкості, у тому числі й тоді, коли модуль швидкості зменшується або коли модуль швидкості залишається незмінним і швидкість змінюється тільки за напрямом.
3. ПРЯМОЛІНІЙНИЙ РІВНОПРИСКОРЕНИЙ РУХ
Прямолінійним рівноприскореним1 рухом називають прямолінійний рух тіла з постійним прискоренням.
Прикладами такого руху є падіння тіл зі стану спокою, якщо можна знехтувати опором повітря, а також рух тіла вздовж похилої площини.
ШВИДКІСТЬ ПРЯМОЛІНІЙНОГО РІВНОПРИСКОРЕНОГО РУХУ
З визначення прискорення 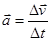 випливає:
випливає: 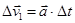
Отже,
під час прямолінійного рівноприскореного руху швидкість тіла за будь-які рівні проміжки часу змінюється на ту ж саму величину.
Позначимо 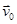 швидкість тіла в початковий момент (при t = 0), а
швидкість тіла в початковий момент (при t = 0), а 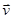 — швидкість тіла в момент часу t. Тоді
— швидкість тіла в момент часу t. Тоді 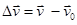 , а
, а 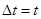 тому формула
тому формула 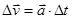 набуде вигляду
набуде вигляду 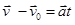 Звідси випливає:
Звідси випливає:
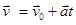
Якщо направити вісь x уздовж прямої, по якій рухається тіло, то в проекціях на вісь x отримаємо:
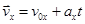
Таким чином, за умови прямолінійного рівноприскореного руху проекція швидкості лінійно залежить від часу. Це означає, що графіком залежності vx (t) є відрізок прямої.
На рис. 3.3 наведено графік швидкості автомобіля, що розганяється, а на рис. 3.4 — автомобіля, що гальмує. Для першого
1 Прямолінійний рівноприскорений рух називають іноді рівнозмінним. Рух з прискоренням, яке дорівнює нулю, ми будемо розглядати як рівномірний прямолінійний рух.
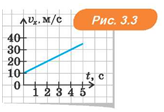 | 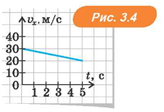 |
автомобіля 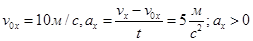 Для другого
Для другого
автомобіля 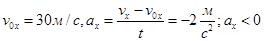
ПЕРЕМІЩЕННЯ ТІЛА ПІД ЧАС ПРЯМОЛІНІЙНОГО РІВНОПРИСКОРЕНОГО РУХУ
Нагадаємо спочатку, що за умови рівномірного руху проекція переміщення sx чисельно дорівнює площі фігури, обмеженої графіком vx (t) і віссю t.
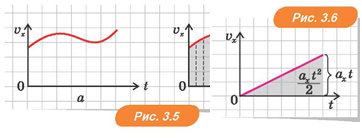
Це справедливо і для нерівномірного руху. Приклад графіка залежності проекції швидкості від часу для такого руху наведено на рис. 3.5, а. Увесь час руху можна розбити на такі малі проміжки часу, що протягом кожного з них рух тіла можна вважати практично рівномірним. Схематично це показано на рис. 3.5, б.
 |
Скористаємося цим, щоб знайти, як залежить переміщення від часу за умови прямолінійного рівноприскореного руху.
Якщо початкова швидкість тіла дорівнює нулю, фігура, обмежена графіком vx (t) і віссю t, — трикутник площею axt2/2 (рис. 3.6).
Користуючись формулою для площі прямокутного трикутника, отримуємо, що
при прямолінійному рівноприскореному русі без початкової швидкості
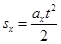
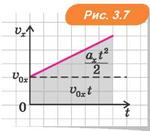
Якщо ж початкова швидкість тіла не дорівнює нулю, то фігура, обмежена графіком vx(t) і віссю t, є трапецією, що складається з прямокутника площею v0xt і трикутника площею axt2/2 (рис. 3.7).
|
Отже,
за умови прямолінійного рівно-прискореного руху з початковою швидкістю v0
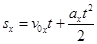
Залежність координати від часу.Оскільки 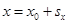 , отримуємо
, отримуємо
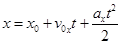
Середня швидкість під час прямолінійного рівноприскореного руху. Користуючись виведеними вище формулами, легко довести, що 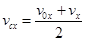
співвідношення спрощує розв'язання багатьох задач.
Співвідношення між переміщенням і швидкістю. Для
розв'язування задач, в умові яких не задано часу руху, корисні формули, що пов'язують переміщення з початковою
і кінцевою швидкостями. З формул 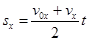 і
і 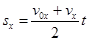 отримуємо:
отримуємо: 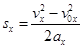 Якщо початкова швидкість дорівнює нулю, ця формула набуває вигляду
Якщо початкова швидкість дорівнює нулю, ця формула набуває вигляду 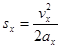
4. ВІЛЬНЕ ПАДІННЯ
Наприкінці 16-го століття італійський учений Ґалілей зробив важливе відкриття: вивчаючи падіння тіл, він виявив на досліді, що коли опором повітря можна знехтувати, то всі тіла, падаючи, рухаються рівноприскорено з однаковим прискоренням.
Дата добавления: 2015-09-11; просмотров: 1749;
