Пересечение прямой с плоскостью
Задача на пересечение прямой с плоскостью является одной из основных задач начертательной геометрии.
Чтобы решить эту задачу в общем виде необходимо знать прием, способ решения (алгоритм). Но если в задаче имеются вырожденные виды оригиналов, то такая задача требует просто развитого пространственного воображения.
Все задачи на пересечение прямой с плоскостью можно разделить на несколько типов:
·Первый тип задач - плоскости имеют вырожденный вид, т.е. являются проецирующими, а прямая является прямой общего положения.
Основным методом решения задач этого типа является метод принадлежности. Рассмотрим ряд примеров.
Пример 3. Построить точку К пересечения прямой l с вертикальной плоскостью Б (рисунок 7- 11).
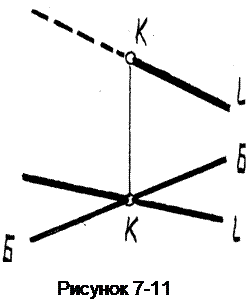 Решение задачи следует начинать с вида сверху, где ответ уже имеется - общая точка для прямой и плоскости находится в месте их пересечения. По виду сверху точки К находим ее на виде спереди.
Решение задачи следует начинать с вида сверху, где ответ уже имеется - общая точка для прямой и плоскости находится в месте их пересечения. По виду сверху точки К находим ее на виде спереди.
Заканчивается решение задачи определением видимости прямой l. На виде сверху все ее участки будут видимы, а на виде спереди будет видим участок, находящийся перед плоскостью, т.е. участок прямой правее точки К. Это легко установитьпредставив положение оригиналов в пространстве.
·Второй тип задач – прямая частного положения и имеет вырожденный вид.
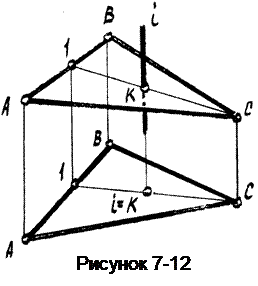 Пример 4. Построить точку пересечения К вертикальной прямой i с плоскостью Б (DАВС), (рисунок 7-12). Т.к. вырожденный вид прямой имеет ся на виде сверху, то решение начинаем с него.
Пример 4. Построить точку пересечения К вертикальной прямой i с плоскостью Б (DАВС), (рисунок 7-12). Т.к. вырожденный вид прямой имеет ся на виде сверху, то решение начинаем с него.
Точка пересечения прямой i с плоскостью Б здесь совпа дает с вырожденным видом самой прямой; i = К.
Чтобы построить т. К на виде спереди проведем на плоскости через т. К (вид сверху) произвольную прямую, например С-1 . Построим эту прямую на виде спереди, и на пересечении прямой С-1 иl находим точку К. Видимость определяем представив (с помощью реконструкции чертежа) взаимное расположение оригиналов.
·Третий тип задач - задачи не содержат элементов частного положения, т.е. прямая и плоскость общего положения (вырожденного вида нет).
В этом случае (рисунок 7-13)решение задачи сводится к рассмотрению взаимного положения двух прямых - данной прямой l и некоторой прямой t, лежащей в плоскости Б.
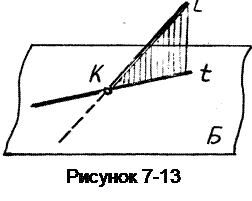 Прямую t выбирают так, чтобы она была конкурирующей с прямой l. Конкурирующие прямые (на одном из видов их изображения совпадают) могут быть либо параллельны, либо пересекаться. Тогда, соответственно, прямая и плоскость, параллельны или пересекаются (см. рисунок 7-10).
Прямую t выбирают так, чтобы она была конкурирующей с прямой l. Конкурирующие прямые (на одном из видов их изображения совпадают) могут быть либо параллельны, либо пересекаться. Тогда, соответственно, прямая и плоскость, параллельны или пересекаются (см. рисунок 7-10).
Алгоритм решения: чтобы определить взаимное положение прямой и плоскости, надо на плоскости провести вспомогательную прямую, конкурирующую с данной и рассмотреть их взаимное положение.
При этом возможны три варианта:
1. если данная прямая сливается с конкурирующей прямой, то прямая принадлежит плоскости;
2. если данная прямая параллельна конкурирующей прямой, то прямая параллельна плоскости;
3. если данная прямая пересекается с конкурирующей прямой, то прямая пересекает плоскость.
Пример 5. Определим взаимное положение прямой и плоскости Б(DАВС), (рисунок 7-14).
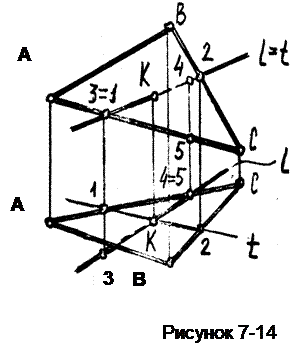 Проводим в плоскости Б прямую t (1,2) фронтально-конкурирующую с данной прямой l.
Проводим в плоскости Б прямую t (1,2) фронтально-конкурирующую с данной прямой l.
По виду сверху определяем, что конкурирующие прямые пересекаются в т. К, которая и является точкой пересечения прямой l с плоскостью Б.Видимость определяем с помощью двух пар конкурирующих точек: 1=3 на виде спереди; точка 3 (принадлежащая l) ближе; на виде сверху из двух точек 4=5, точка 4 выше точки 5.
На одном из видов видимость можно определить и по положению плоскости Б.
Дата добавления: 2015-11-06; просмотров: 1232;
