ОПРЕДЕЛЕНИЕ ДЛИНЫ ОТРЕЗКА И УГЛОВ ЕГО НАКЛОНА К ПЛОСКОСТЯМ УРОВНЯ.

При решении различных общегеометрических задач часто возникает необходимость определения натуральной величины отрезка по его комплексному чертежу.

Если отрезок принадлежит прямой уровня - горизонтали, фронтали или профильной прямой, то в этом случае натуральная величина отрезка имеется на одном из видов:

· для горизонтали - на виде сверху;

· для фронтали - на виде спереди;

· для профильной прямой - на виде слева.

Если же отрезок принадлежит прямой общего положения, то на всех проекциях (видах спереди, сверху, слева) его изображение будет меньше самого отрезка.

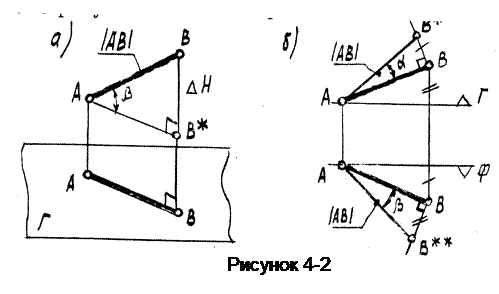
Для определения натуральной величины отрезка и углов наклона его к плоскостям уровня применяют способ прямоугольного треугольника (рисунок 4-2).

Рассмотрим DАВВ*(рисунок 4-2). Здесь АВ=çАВ÷; ВВ*=DН (разность высот точек А и В - концов отрезка.); АВ*= АВ (проекция отрезка).

Таким образом если, имея комплексный чертеж отрезка, мы сумеем построить прямоугольный треугольник катетами которого будут –1)одна из проекций отрезка и 2)разность измерений концов отрезка, отмеряемых от соответствующей первому катету плоскости проекций (от Г- высот, от Ф - глубин, от П – широт), то гипотенуза полученного треугольника будет равна натуральной величине отрезка.

При этом угол между гипотенузой треугольника и проекцией отрезка равен углу наклона отрезка к плоскости проекций (Г, Ф, или П соответственно), (рисунок 4-2б).

Строить такой прямоугольный треугольник по двум катетам можно в любом удобном месте чертежа.

Пример 1.Определить угол наклона отрезка АВ к фронтальной плоскости (рисунок 4-3).

Для определения указанного угла удобно построить прямоугольный треугольник, приняв фронтальную проекцию отрезка в качестве его первого катета. Вторым катетом треугольника в этом случае будет разность глубин концов отрезка измеренная на горизонтальной проекции (виде сверху).

Угол α между первым катетом и гипотенузой и будет искомым. Попутно определится и длина отрезка равная длине гипотенузы треугольника.

Пример 2. Отложить на проекциях прямой m от точки А отрезок АВ, натуральная величина которого равна 50 мм (рисунок 4-4).Можно предложить такой способ решения задачи. Возьмем на указанной прямой произвольную точку С и определим натуральную величину полученного отрезка АС способом прямоугольного треугольника.

Поскольку на гипотенузе треугольника имеем натуральные длины отрезков, отложим здесь от точки А заданную величину 50 мм. Затем проведем прямую параллельно второму катету треугольника до пересечения с проекцией отрезка АС.

Полученная точка будет являться искомой точкой В. Вторую проекцию точки В находим проецируя точку В на вторую проекцию отрезка.