Развертка конической поверхности

Развертка поверхности пирамиды

Развёртка такой поверхности представляет собой плоскую фигуру, которая получается совмещением всех её граней с одной плоскостью.

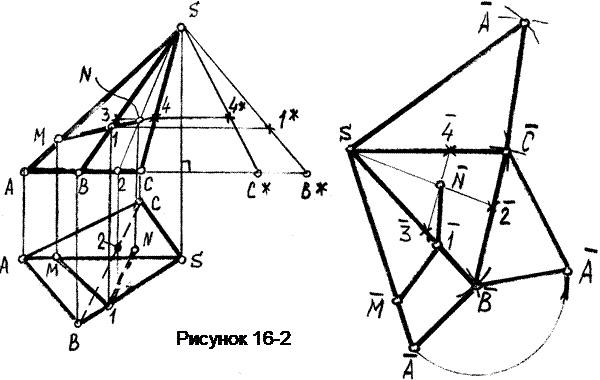
Пример 1. Построить развёртку поверхности пирамиды АВСS (рисунок 16-2) и нанести на неё линиюМN.

Так как боковыми гранями пирамиды являются треугольники, то для построения развёртки необходимо найти натуральный вид этих треугольников, для чего следует определить истинные длины сторон - ребер пирамиды.

Основание пирамиды лежит в горизонтальной плоскости, следовательно, натуральная величина ребер АВ, ВС и АС уже имеется на чертеже.

Ребро SA является фронталью, поэтому на виде спереди оно изображается в натуральную величину.

Натуру ребер SВ и SС определяем способом прямоугольного треугольника. Одним катетом его является превышение точки S над точками В и С, а вторым - вид сверху ребер SВ и SС.

Затем по трём сторонам строим последовательно все боковые грани пирамиды.

Для нанесения на развёртку линии МN вначале определим истинную величину отрезков AM и В1 и отложим их на развёртке на соответствующих ребрах.

Чтобы нанести точку М, проведём на грани SВС прямую S2 и найдём её положение на развёртке, отложив отрезок В2 (замеренный на виде сверху) на стороне ВC. Затем на виде спереди проведём через точку 4 отрезок 3-4, параллельный ребру ВС и найдём его положение на развёртке, для чего отложим отрезок C4 на стороне SС и через полученную точку проведём прямую 3-4 параллельную ребру ВС. На пересечении прямых S-2 и 3-4 найдём точку N. Соединив полученные точки М, 1, N получим искомую линию.

Развертка конической поверхности

Для построения развёртки конической поверхности необходимо вписать в неё (или описать около неё) многогранную поверхность, т.е. заменить поверхность вращения многогранной поверхностью.

В этом случае поверхность разбивается на треугольники, и такой способ построения развёрток называется способом треугольников(способ триангуляции).

Пример 2. Построить развёртку боковой поверхности эллиптического конуса (рисунок 16-3) и нанести на неё точку М.

Заменим данную коническую поверхность поверхностью вписанной двенадцатиугольной пирамиды. Развёртка пирамиды будет состоять из ряда примыкающих друг к другу треугольников. То есть. построение развертки конуса сводится к построению развертки пирамиды (см. выше).

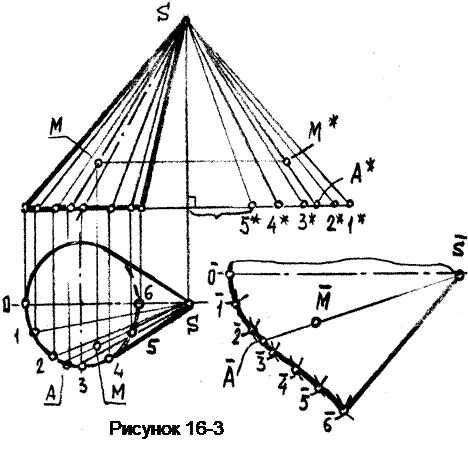Для построения натурального вида этих треугольников необходимо определить натуральные величины образующих конуса (проведённых в точки деления основания) способом прямоугольного треугольника.

Натура сторон треугольника, лежащих в основании конуса равна хорде стягивающей дугу окружности: 1-2 = 2-3 = 3-4 = и т.д., и на виде сверху изображается в натуральную величину. Так как развёртка представляет собой симметричную фигуру, то построим развёртку только половины поверхности конуса.

После построения развёртки находим на ней положение точки М. Для этого проведём через точку М образующую конуса АS, определим её натуру и положение точки М на ней (отрезок А*М*). Затем находим положение образующей АS на развёртке, для чего замеряем на виде сверху хорду А2 и откладываем её на развёртке от точки 2 в сторону точки 3. Соединяем точку А с точкой S и на этой прямой откладываем отрезок A*М*.

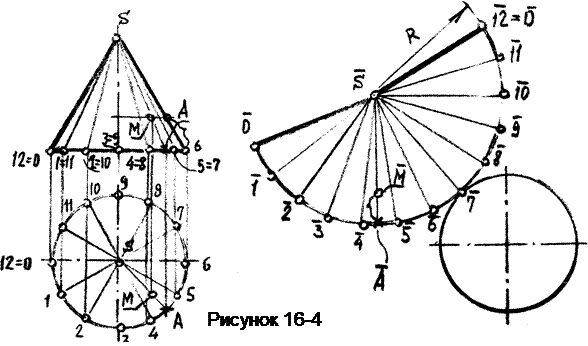
Пример З. Построить развёртку поверхности прямого кругового конуса и нанести на нее точку М (рисунок 16-4).

Развёртка боковой поверхности кругового конуса представляет собой круговой сектор, радиус которого равен натуральной величине образующей конуса, а длина дуги равна длине окружности основания конуса. Практически длину дуги определяют длинами хорд, стягивающих дуги основания (1-2 = 2-3 = 3-4 = и т.д.), замеренными на виде сверху. Построение точки М на развёртке аналогично примеру 2.