Лекция 5. Диэлектрики в электрическом поле.
§ 5-1 Электрический диполь.
В проводниках электрические заряды свободны, т.е. они могут перемещаться по все-му проводнику. Диэлектрики же характеризуются прежде всего тем, что в них нет свобод-ных зарядов, и они не могут проводить электрический ток. В этом классе веществ заряды находятся в связанном состоянии, однако, центры распределения положительного и отрица-тельного зарядов, вообще говоря, могут не совпадать. Диэлектрики, в которых такое несов-падение имеет место, называются полярными. Система, состоящая из двух равных по величине, но противоположных по знаку зарядов, находящихся на расстоянии l друг от друга, называется электрическим диполем. Для описания свойств диполя вводится так на-
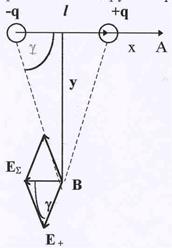 Рис.12. Поле диполя.
Рис.12. Поле диполя.
| зываемый дипольный момент р =ql, где l – вектор, проведенный из центра отрицательного заряда к центру положительного. Хотя в целом диполь нейтрален, тем не менее несовпадение центров положительного и отрицательного зарядов приводит к тому, что вокруг диполя образуется электрическое поле. Его можно вычислить по принципу суперпозиции. Наиболее просты расчеты для двух случаев: вычисления поля вдоль оси диполя и для точки, находящейся на перпендикуляре, восстановленным из середины l. Пусть точка А, где требуется найти поле диполя, отстоит от положительного заряда на расстояние х. Тогда напряженность поля от этого заряда в точке А равна:
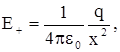
|
а от отрицательного q 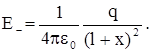
Общее поле Е0 двух зарядов равно (см. рис.12)
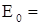
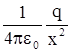 -
- 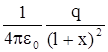 =
= 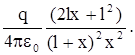
Для расстояний х>> l выражение для Е0 упрощается: (l+x)» x и
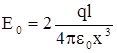 .
.
Для вычисления напряженности в точке В достаточно вспомнить, что меньшая диагональ ЕS ромба (см рис12) со стороной Е+ равна ЕS =2Е+сosg .Кроме того, из рис.12 следует, что
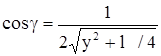 ; и
; и
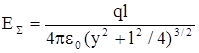 »
» 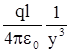 .
.
Поскольку величина Е непрерывна, то при переходе от точки А к точке В значение Е должно меняться постепенно, и для произвольной точки можно показать, что
Е0 = 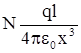 ,
,
где N – некий поправочный коэффициент, меняющийся от 1 до 2 при изменении положения точки. Точный расчет показывает, что N = 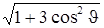 , где
, где 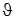 - угол между направлением радиуса- вектора точки и осью диполя. В рамках нашего курса этот расчет проводиться не будет.
- угол между направлением радиуса- вектора точки и осью диполя. В рамках нашего курса этот расчет проводиться не будет.
 § 5-2 Механизмы поляризации.
§ 5-2 Механизмы поляризации.
Кроме полярных диэлектриков существуют вещества, в которых центры положитель-ных и отрицательных зарядов совпадают друг с другом в отсутствии внешнего поля.
Такие вещества называют неполярными диэлектриками. Однако, под действием внеш-него поля у них наблюдается небольшое смещение зарядов. Молекулы диэлектрика как бы раздвигаются: заряды в ней смещаются в разные стороны, и образуются электрические диполи. В полярных и неполярных диэлектриках внешнее электрическое поле оказывает
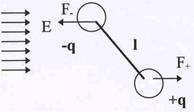 Рис.13. Ориентирующее
действие на диполь внеш-него поля.
Рис.13. Ориентирующее
действие на диполь внеш-него поля.
| ориентирующее действие на каждый диполь. Как следует из рис.13, возникает вращающий момент, под действием кото-рого все диполи стремятся выстроиться вдоль направления поля.Однако этому стремлению противодействуют различные причины: внутренние силы, действующие между молекулами, тепловое движение молекул и т.п. Поэтому возникает некоторая преимущественная пространственная ориентация диполей, степень которой характеризуется вектором поляризации, определяемым как суммарный дипольный момент единицы объема, т.е. |

 Р =
Р = 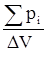 ;
;
для большинства диэлектриков эта величина оказывается незначительной, и ее можно считать пропорциональной напряженности внешнего поля Р = ke0 Е. Величина k (каппа) на-зывается диэлектрической восприимчивостью. Разбиение коэффициента пропорцио-нальности на два сомножителя kи e0 связано с требованиями размерности в системе СИ.
§ 5-3 Теорема о поляризационных зарядах.
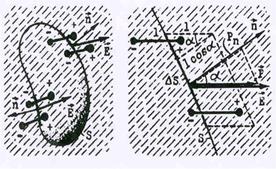 Рис.14.Вычисление поляризационно-го заряда.
Рис.14.Вычисление поляризационно-го заряда.
| Рассмотрим некоторую область внутри диэлек-трика, ограниченную поверхностью S (см.рис.14). При поляризации происходит смещение положи-тельных зарядов в направлении напряженности и отрицательных – в противоположном. Как видно из рис.14, через те участки поверхности, где на-пряженность направлена внутрь поверхности, часть отрицательных зарядов покинет рассма-триваемую область, а через участки, где напря-женность направлена наружу, в область войдет отрицательный заряд. Если вошедший и вышед-ший заряды не равны друг другу, то область при- |
оретет поляризационныйзаряд Qп. Для участка поверхности DS (правая часть рис.14) через DS войдут отрицательные заряды тех и только тех молекул, которые находятся в параллелепипеде с площадью основания DS и высотой lcosa, где l – величина возможного смещения зарядов в молекуле, а a - угол между внешней нормалью к поверхности и вектором поляризации. Объем параллелепипеда равен DS lcosa, следовательно в нем находится n0DS lcosa молекул (n0 –концентрация молекул). При этом левому основанию параллелепипеда должна соответствовать внешняя нормаль, направлен-ная налево (угол a - тупой), а для правого основания - угол a - острый. Через левое основа-ние выходит, а через правое – входит отрицательный заряд. Поэтому и для левого и для правого оснований появится знак минус, т.е. D Qп = - q n0DS lcosa ( q- заряд каждой моле-кулы). Учитывая, что q n0 l = Р0 – величина вектора пояризации и Р0 cosa=Рn , получим: D Qп = - Рn DS.
Интегрируя это выражение по всей замкнутой поверхности S, имеем:
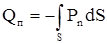 .
.
Полученная формула, вообще говоря, спаведлива для неоднородного диэлектрика. Для однородного же поляризационные заряды могут возникать только на поверхности, причем поверхностная плотность зарядов s = D Qп /DS = Pn . Действительно, подставляя в послед-нее выражение значение Pn =e0 kEn , нетрудно получить, что
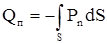 = -
= - 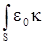
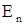 dS
dS 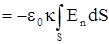 ; но по теореме Гаусса
; но по теореме Гаусса 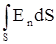 =
= 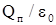 и
и
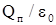 = -
= - 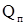 ; при k> 0 , это может выполняться лишь при
; при k> 0 , это может выполняться лишь при 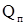 = 0.
= 0.
§ 5-4 Вектор электрического смещения.
Из изложенного ясно, что в диэлектриках кроме внешнего поля существует еще и соб-ственное (внутреннее) поле, поэтому можно ожидать, что Еполн = Есвоб + Епол . Однако, принцип суперпозиции в общем случае здесь не пригоден, т.к. он справедлив лишь для определенно заданного распределения зарядов, в то время как распределение зарядов в диэлектрике само определяется искомым электрическим полем. Поэтому каждое из слагаемых должно быть определено из каких-то других соображений.
Рассмотрим замкнутую поверхность, внутри которой есть свободные Qс и поляриза-ционные Qп заряды. Тогда теорема Гаусса принимает следующий вид:
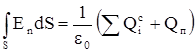 .
.
Заменяя величину Qп согласно теореме о поляризационных зарядах, можно найти:
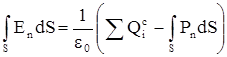 .
.
Домножим обе части последнего уравнения на e0 и перенесем интеграл из правой части в левую. Получаем, что
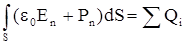 .
.







 Выражение, стоящее в круглых скобках под знаком интеграла, представляет собой новый вектор D =e0 E + P, называемый вектором электрического смещения или вектором электрической индукции. Его можно представить так:
Выражение, стоящее в круглых скобках под знаком интеграла, представляет собой новый вектор D =e0 E + P, называемый вектором электрического смещения или вектором электрической индукции. Его можно представить так:
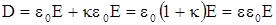 ,
,

 где (1+k) = e называют относительной диэлектрической проницаемостью вещества. Тогда D = ee0E.
где (1+k) = e называют относительной диэлектрической проницаемостью вещества. Тогда D = ee0E.
Для вектора электрического смещения теорема Гаусса такова 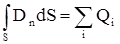 .
.
Дата добавления: 2015-11-06; просмотров: 1128;
