Общая постановка задачи принятия решения

Задачей принятия решения назовём пару (Ω, P) , где Ω – множество вариантов, P – принцип оптимальности. Решением задачи (Ω, P) является множество Ω_p ≤ Ω, полученное с помощью принципа оптимальности P. Отсутствие хотя бы одного из элементов лишает смысла задачи в целом. Если нет Ω не из чего выделять Ω_p. Если нет P, то найти Ω_p невозможно. Математическим выражением принципа оптимальности P служит функция выбора C_p. Она сопоставляет любому подмножеству X ≤ Ω его часть C_p(X). Решением Ω_p исходной задачи и является множество C_p(X). Задачи принятия решений различаются в зависимости от имеющейся информации о множестве Ω и принципе оптимальности P. В общей задаче принятия решений как Ω, так и P могут быть неизвестными.

Информацию, необходимую для выделения Ω_p получают в процессе решения.

Задачу с известными Ω называют задачей выбора, а задачу с известнми Ω из P - общей задачей оптимизации.

Таким образом, задача выбора и задача оптимизации являются частными случаями общей задачи принятия решений. В общем случае для задачи выбора необязательно необходимо полное восстановление принципа оптимальности, а можно ограничиться только информацией, достаточной для выделения Ω_p. Общая задача оптимизации не обязательно требует минимизации одной или нескольких числовых функций, так как может быть и так, что другим способом выделяется множество лучших элементов, то есть выделяются значения C_p(Ω) при заданных Ω и C_p. Если C_p - скалярная функция на множестве Ω, то получаем обычную оптимизационную задачу.

Элементы множества Ω называются альтернативами или вариантами.

Принцип оптимальности P задаёт понятие лучших альтернатив: лучшими считают альтернативы, принадлежащие C_p(Ω). В практических задачах альтернативы обладают многими свойствами, оказывающими влияние на решение.

Пусть некоторое свойство альтернатив из Ω выражается числом, то есть существует отображение φ: Ω→ E₁. Тогда такое свойство называется критерием, а число φ(x)-оценка альтернативы x по критерию. Одновременный учёт отдельных свойств может быть затруднительным. При этом можно выделить группы свойств, которые агрегируют в виде аспектов. Аспект – сложное свойство альтернатив, которое одновременно учитывает все свойства, входящих в группу. В частном случае аспект может являться критерием.

Пусть все свойства k₁, …, k_m, учитываемые при решении задач (Ω, P) являются критериями. Критериальным пространством называют пространство E_m, координаты которого есть оценки соответствующих критериев.

Пример: при определении маршрута перевозок альтернативы - маршруты.

Диспетчер учитывает свойства: протяженность, загрузка, энергоёмкость, безопасность, техническое обслуживание и другое.

Техническое обслуживание – это число станций, сроки выполнения ремонтных работ и так далее. Следовательно, техническое обслуживание – это аспект.

Стоимость маршрута состоит из стоимости топлива, обслуживания и т.д. То есть это тоже аспект. Однако, так как стоимость можно вычислить, то это критерий (но так будет не всегда).

Сформулируем схему процесса принятия решения.

Формируется множество Ω, его подготавливают для последующего решения задачи выбора (при назначении на должность сначала готовят список кандидатов, а затем назначают лицо из этого списка).

Для формирования Ω используют условия возможности и допустимости альтернатив, которые определяют конкретными ограничениями задачи. При этом считают известным универсальное множество альтернатив Ω_y. Таким образом, задача формирования Ω является задачей выбора (Ω_y, P₁) , где P₁ – принцип оптимальности, выражающий условия допустимости.

Множество 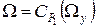, полученное в результате решения, рназывают исходным множеством альтернатив (ИМА) (Ω_y – все специалисты, Ω - специалисты, удовлетворяющие требованиям ).

Таким образом, общая задача принятия решения сводится к решению

двух последовательных задач выбора.

В процессе решения участвует лицо, принимающее решение (ЛПР), экс-

перты, консультанты.

ЛПР – человек, имеющий цель, служит мотивом постановки задачи. ЛПР

имеет полномочия и несёт ответственность. Основная функция ЛПР выделять Ωp. ЛПР даёт информацию о принципе оптимальности P.

Эксперт - не несёт ответственности, он даёт оценки альтернатив, необходимые для формирования ИМА и решения задачи выбора.

Консультант – специалист по теории выбора и ПР. Он разрабатывает модель, процедуру принятия решений , организует работу ЛПР и экспертов.

В простейшем случае задачу (Ω, P) решает непосредственно ЛПР.

Прикладные результаты ТПР имеют вид алгоритмов решения задач.

Часть алгоритмов может быть реализована вручную, но основная часть ориентирована на диалоговый режим работы ЭВМ или на применение в экспертных системах.