Спецификация модели. Парная регрессия применяется для моделирования зависимости, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной.

Парная регрессия применяется для моделирования зависимости, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной.

Для выбора вида аналитической зависимости можно использовать следующие методы:

– графический (вид зависимости определяется на основе анализа поля корреляций);

– аналитический (на основе качественного анализа изучаемой взаимосвязи);

– экспериментальный (построение нескольких моделей различного вида с выбором наилучшей согласно применяемому критерию качества).

Визуальный анализ поля корреляций (рис. 2.1) позволяет определить форму кривой регрессии, ее особенности. Зная типичный вид графиков различных функций можно подобрать соответствующую аналитическую зависимость.

Примером применения аналитического метода может служить зависимость между затратами (y) и объемом производства (x). Считая, что затраты прямо пропорциональны объему производства, зависимость между ними можно представить в виде линейной функции

,

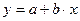где a– часть затрат, не зависящая от объема производства, b – дополнительные затраты на производство единицы продукции.

Разделив обе части последнего уравнения на объем производства x, получим зависимость удельных затрат (z = y/x) на производство единицы продукции от объема производства

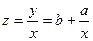
При построении модели зависимости спроса товар от его цены при выборе вида зависимости следует учитывать, что при увеличении цены спрос падает. В этом случае могут использоваться следующие зависимости:

, ;

, ;

, .

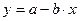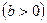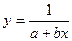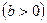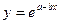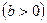Если из соображений экономической теории следует, что величина изменения зависимой переменной y пропорциональна значению независимой переменной x, то можно выбрать полиномиальную, степенную или показательную зависимости (см. п. 2.1).

Если предполагается, что значение зависимой переменной y при увеличении значения независимой переменной x не может превысить некоторого предела, то можно выбрать гиперболическую 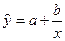 или логистическую 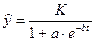зависимости.

В случае, если в рассматриваемой области изменения фактора x результативная переменная y принимает минимальное или максимальное значение, в уравнение регрессии включают переменные x не только первой, но и второй степени, например

.

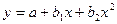В качестве критерия качества модели может использоваться либо средняя квадратическая ошибка модели 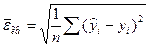, либо остаточная дисперсия .

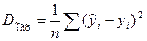Этот подход легко реализуем при наличии соответствующих вычислительных средств. Но он не является определяющим, так как в эконометрике более важным является не способность модели соответствовать имеющемуся массиву данных наблюдений, а ее способность раскрывать существующие закономерности в экономических явлениях и процессах и интерпретация полученных с ее помощью результатов.