Основное уравнение динамики вращательного движения.
Рассмотрим систему материальных точек, каждая из которых может перемещаться, оставаясь в одной из плоскостей, проходящих через ось Z (рис. 4.15). Все плоскости могут вращаться вокруг оси Z с угловой скоростью 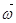 . Тангенциальная составляющая скорости i-ой точки может быть записана в виде:
. Тангенциальная составляющая скорости i-ой точки может быть записана в виде: 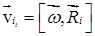 .
.
Тогда, учитывая, что
 ОПРЕДЕЛЕНИЕ: моментом импульса относительно оси Z называется составляющая
ОПРЕДЕЛЕНИЕ: моментом импульса относительно оси Z называется составляющая 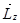 по этой оси момента импульса
по этой оси момента импульса 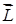 относительно точки «О», лежащей на оси (рис. 4.16):
относительно точки «О», лежащей на оси (рис. 4.16): 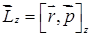 , можно показать, что
, можно показать, что 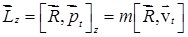 , где
, где 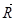 – составляющая радиус-вектора
– составляющая радиус-вектора 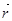 , перпендикулярная оси Z;
, перпендикулярная оси Z; 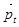 – составляющая вектора
– составляющая вектора 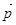 , перпендикулярная к плоскости, проходящей через ось Z и точку «m».
, перпендикулярная к плоскости, проходящей через ось Z и точку «m».
Подставив значение для 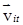 в формулу для
в формулу для 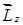 получим выражение для момента импульса точки относительно оси Z:
получим выражение для момента импульса точки относительно оси Z:
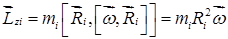 .
.
Это можно записать, воспользовавшись свойством двойного векторного произведения и учтя, что векторы 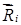 и
и 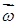 взаимно перпендикулярны.
взаимно перпендикулярны.
Просуммировав это выражение по всем точкам и вынося общий множитель 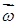 за знак суммы (S), найдем для момента импульса системы относительно оси Z следующее выражение:
за знак суммы (S), найдем для момента импульса системы относительно оси Z следующее выражение:
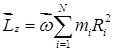 ,
,
где 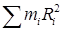 – момент инерции системы материальных точек относительно оси Z.
– момент инерции системы материальных точек относительно оси Z.
Тогда 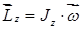 . Учитывая, что
. Учитывая, что 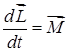 , получаем
, получаем

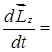
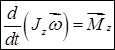 . (4.3)
. (4.3)
Это основное уравнение динамики вращательного движения. По форме оно сходно с уравнением II-закона Ньютона: 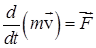 .
.
Абсолютно твердое тело можно рассматривать как систему материальных точек с неизменными расстояниями между ними. Для такой системы момент инерции 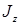 есть величина постоянная относительно фиксированной оси. Следовательно, для абсолютно твердого тела основное уравнение динамики вращательного движения примет вид:
есть величина постоянная относительно фиксированной оси. Следовательно, для абсолютно твердого тела основное уравнение динамики вращательного движения примет вид:
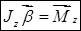 , (4.4)
, (4.4)
где 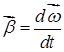 – угловое ускорение тела;
– угловое ускорение тела;
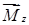 – результирующий момент внешних сил, действующих на тело.
– результирующий момент внешних сил, действующих на тело.
Сопоставив уравнения динамики вращательного движения с уравнениями динамики поступательного движения, легко заметить, что при вращательном движении роль силы играет момент силы, роль массы – момент инерции и т.д. (см. таблицу).
| Поступательное движение | Вращательное движение |
| 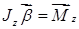
|
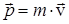
| 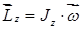
|
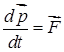
| 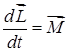
|
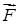 – сила – сила
| 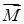 или или 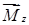 – момент силы – момент силы
|
| m – масса | 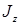 – момент инерции – момент инерции
|
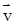 – линейная скорость – линейная скорость
| 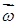 – угловая скорость – угловая скорость
|
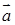 – линейное ускорение – линейное ускорение
| 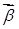 –угловое ускорение –угловое ускорение
|
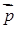 – импульс – импульс
| 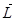 –момент импульса –момент импульса
|
Все приведенные выше формулы справедливы для случая, если ось вращения тела неподвижна.
Дата добавления: 2015-11-04; просмотров: 905;
