Фраунгофер дифракциясы. Фраунгофер дифракциясының Френель дифракциясынан негізінде айырмашылығы жоқ.

Фраунгофер дифракциясының Френель дифракциясынан негізінде айырмашылығы жоқ.

Шексіз ұзын, ені b саңылауға жазық жарық толқыны нормаль (тік) иүсетін болсын (1-сурет). Саңылау ұзындығының оның енінең көп үлкен болуы іс жүзінде оны шексіз ұзын деп санауға жеткілікті. Мәселен, ені 0,001-0,02 мм болған жағдайда бірнеше миллиметр ұзындықты шексіз деп санауға болады.

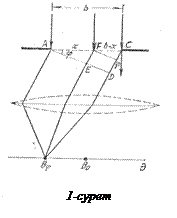
Саңлаудан кейін линза, ал оның тоғыстық жазықтығына L бақылау қалқасы қойылған. Жарық түзу сызықты таралған жағдайда линзаның тоғыстық жазықтығында шексіз жіңішке жарық жолақ алынған болар еді. Шындығында толқындық шептің саңлауға жеткен әрбір нүктесі барлық жаққа таралатын екінші реттік толқындардың көзі болады. Жарықтың бастапқы бағытымен қайсыбір j бұрыш жасап тұратын сәулелер линзаның тоғыстық жазықтығындағы B_j нүктесіне жиналады.

Тербелістердің B_j нүктедегі амплитудасын есептеу үшін толқындық беттің ашық бөлігін ендері бірдей саңылау нүктелеріне параллель жіңішке жолақтар түріндегі аумақтарға бөлеміз. Осы аумақтардың әрқайсысы B_j нүктесіне келіп жететін толқындар көзі ретінде қарастырылуы тиіс, және көрші аумақтардан шығарылатын толқындардың фазалары бірдей шамаға өзгеше болады. Өйткені жарық нормаль (тік) бағытта түскенде саңылау жазықтығы толқын бетімен дәл келеді. Элементар толқындардың амплитудалары бірдей болады, өйткені аумақтардың аудандары тең және бақылау бағытына көлбеуліктері де бірдей.

Осы екі жағдай – амплитудалардың теңдігі және аумақтан аумаққа өткенде фазалардың бірдей шамаға өзгеруі – қарастырылып отырған есептің аналитикалық та, график арқылы да амалмен шешілуін оңайлатады.

1. Алдымен еcепті шешудің аналитикалық амалын қарастырайық. Ол үшін толқындық беттің бөлігін ені dx элементар аумақтарға бөлеміз. Қалқаның кезкелген нүктесінде dx аумағы қоздыратын тербелістің dA амплитудасын dA=сdx түрінде өрнектеуге болады, мұндағы с–пропорциялық коэффициент, ол j бұрышқа тәуелді емес.

Қалқаның қайсыбір нүктесіне барлық аумақтардан келетін тербелістер амплитудаларының алгебралық қосындысын А₀ арқылы белгілейміз. Мұны dA-ны түгел саңылау бойынша интегралдап табуға болады. .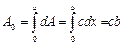

Осыдан коэффициент 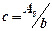, демек, 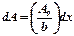болады. Сонымен, саңылаудың тиісті бөлігіндегі жарықтың ұйытқуы мына қатынаспен өрнектеледі

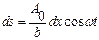(1)

Түсетін толқын бағытымен j бұрыш (дифракция бұрышы) жасайтын бағытында саңылаудың түгелдей әрекетін табу үшін әртүрлі аумақтардан B_j бақылау нүктесіне дейін жететін толқындарды сипаттайтын фазалар айырымын ескеру қажет. Бұл үшін дифракцияланған сәулелердің бағытына перпендикуляр АD жазықтығын жүргіземіз (1-сурет). Осы жазықтықта орын алатын фазалардың үлестірілуі B_j нүктесіне дейін келіп жететін элементар толқындардың фазаларының қатынасын анықтайды. Сонымен AC жазықтығынан AD жазықтығына дейінгі жолда пайда болатын жол айырымын тағайындау жеткілікті болады. 1-суреттен А нүктесіне (аумақтың сол жақ шеті) және А нүктесінен х қашықтықта жататын қандайда бір F нүктесіне жапсарлас элементар аумақтан келетін толқындар арасындағы жол айырымы мынаған тең: FE=xsinj.

B_j нүктесінде толқындық беттің барлық ашық бөлігі туғызатын қорытқы ұйытқу саңылаудың бүкіл ені бойынша алынған интегралмен (яғни х-тың 0-ден b-ға дейінгі барлық мәндері бойынша) өрнектеледі

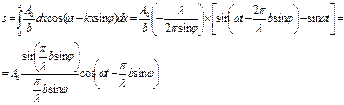(2)

(2) өрнектегі косинустың алдында тұрған өрнектің модулі қорытқы толқынның В_j нүктедегі А_j амплитудасын береді:

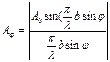(3)

(3) өрнегін зерттейік. Саңылаудың ортасында жататын нүкте үшін (линзаның центріне қарсы нүкте) дифракция бұрышы j=0. (3) формуласына j=0 мәнін қойып 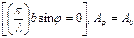болатынын табамыз, яғни j=0 болғанда барлық элементар аумақтардан шығарылатын толқындар B_j нүктеге бірдей фазада келіп жетеді. Сондықтан қорытқы толқынның амплитудасы қосылатын толқындардың амплитудаларының алгебралық қосындысына тең.

j мәндері 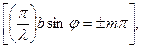мұндағы 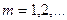шартын қанағаттандыратын жағдайда, яғни егер

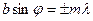(4)

болған жағдайда А_j амплитуда нөлге айналады.

Сонымен, (4) шарты интенсивтік минимумдерінің орнын анықтайды. Бірінші минимум 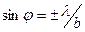шартын қанағаттандыратын бұрышта байқалатын болады.

Минимумдердің араларында орталық максимумнан шамасы бойынша елеулі түрде кем түсетін интенсивтіктің екінші реттік максимумдары орналасады. Осы максимумдар j мәндері мына шарттарды

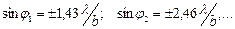(5)

қанағаттандыратын жағдайда пайда болады.

Жарық интенсивтігі амплитуда квадратына пропорционал. Демек,

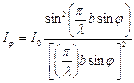(6)

мұндағы I₀-дифракциялық суреттің ортасындағы жарық интенсивтігі ( 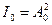); I_j-j бұрышының берілген мәнімен орны анықталатын нүктедегі жарық интенсивтігі.

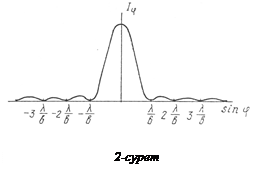
(6) функциясының графигі 2-суретте кескінделген. Минимумдар саны b-саңылау енінің және l толқын ұзындығының қатынасына тәуелді. Екінші реттік максимумдар шамасы тез төмендейді. Егер I₀=1 деп алсақ, ал екінші реттік максимумдарды I₁, I₂, I₃,... арқылы белгілесек, онда I₀: I₁: I₂:...=1:0,045:0,016:... болады. Сонымен, негізгі жарық ағыны 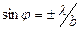(орталық максимум) мәндерімен анықталатын аралыққа шоғырланғанымен, оның қайсыбір бөлігі бірінші (энергияның ~5%) және екінші (энергияның ~2%) максимумдар және т.т. бағыттарында таралады.

Алынған қатынастардан максимумдар мен минимумдардың орны l толқын ұзындығына тәуелді болатындығы көрінеді. Сондықтан қарастырылған дифракциялық суреттің түрі тек монохромат жарық үшін орындалады. Ақ жарық жағдайында бірі екіншісіне қатысты l толқын ұзындығының айырмашылығына сәйкес ығысқан әртүрлі түстер үшін дифракциялық суреттердің жиынтығы байқалады. Орталық максимум (j=0) барлық толқын ұзындықтары үшін ортақ болады, осыдан дифракциялық суреттің центрі ақ жолақ түрінде шығады, мұның сол және оң жақтарында түрлі-түсті жолақтар орналасады.