Дифракциялық тор
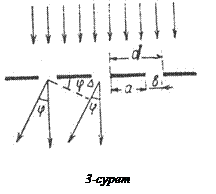
Бірдей дифракциялық элементтердің бір-бірінен бірдей қашықтықтарда орналасқан жиынтығы дифракциялық торды құрайды. Біз дифракциялық элементтері ені а мөлдір емес аралықтармен бөлінген ені b параллель саңылаулар болатын дифракциялық торды қарастырамыз. а+ b=d шамасын тордың периоды немесе тұрақтысы деп атайды. N саңылаудан тұратын осындай торға жазық монохроматты толқын нормаль түсетін болсын. Барлық N саңылау жататын жазықтыққа нормальмен j бұрыш жасайтын бағытта таралатын жарық интенсивтігін табу керек (3-сурет).
Екі саңылаудағы дифракциямен ұқсастығы бойынша, N саңылаудың әрқайсысынан алынатын дифракциялық сурет (3.33-суретте көрсетілген графикпен бейнеленетін) қалқадағы бір орынға келетіндігін атап өтеміз. Сондықтан, егер әртүрлі саңылаулардан бақылау нүктесіне келетін элементар толқындар когерентті болмаса, онда N саңылаудан алынатын қорытқы дифракциялық суреттің бір саңылау жасайтын дифракциялық суреттен бір-ақ айырмашылығы болар еді-барлық интенсивтіктер N есе өсер еді. Бірақта саңылаулардан шығатын толқындар когерентті болады, сондықтан бұлардың араларындағы интерференцияны ескеру керек болады.
3-суреттен екі көрші саңылаудың сәулелері арасындағы D жол айырымы мынаған тең болатындығы көрінеді
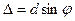(1)
Көп жарық шоқтарының көп саны интерференцияланғанда жол айырымы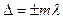 
, мұндағы m=0, 1, 2,… болған жағдайда интенсивтіктері бірдей максимумдар қатары пайда болады. (1) қатынасынан
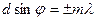(2)
шартын қанағаттандыратын j бұрышы мәндері жағдайында максимумдар қатары пайда болады.
Егер тордағы саңылаулар саны N-ге тең болса, онда бас максимумдар араларына N-1 минимумдер орналасатын болады. Осы минимумдер орындарын мына шарт анықтайды:
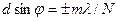(3)
мұндағы m=1, 2, 3,… (3) минимумдер шарты (2) максимумдар шартына айналатын m= N, 2N, 3N,… болатын жағдайлардан басқа.
Осы минимумдер бір саңылаудан алынатын
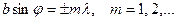(4)
шартын қанағаттандыратын минимумдерден өзгеше, қосымша минимумдер деп аталады.
Сонымен, N саңылаудың дифракциялық толық суреті мына шарттардан анықталады.
бұрынғы минимумдер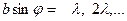 
қосымша минимумдер
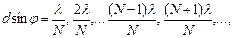
бас максимумдар
,
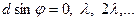Қосымша минимумдер араларына екінші реттік әлсіз максимумдар орналасады. Көрші бас максимумдар аралығына келетін осындай максимумдар саны (N-2)-ге тең. Бұлардың интенсивтігі ең жақын бас максимум интенсивтігінің 1/23-нен артпайды.
 |
N шоқ интерференцияға түскенде алынатын I1 интенсивтіктің үлестірілуі 4а-суретте келтірілген. Жеке саңылаулардан келетін шоқтардың интерференциясын ғана ескергенде бас максимумдар бірдей интенсивтікке ие болуы тиіс еді. Шындығында саңылаулардың әрқайсысынан әртүрлі j бұрыштарымен дифракцияланатын сәулелер қалқада амплитудалары әртүрлі тербелістер беруі нәтижесінде бас максимумдардың шамалары бірдей болмайды. Осы айырмашылықты ескеру үшін бір саңылаудағы дифракция жағдайындағы I2 интенсивтіктің үлестірілуін пайдалану керек (4б-сурет). Сонда жарықталудың нағыз үлестірілуі I=I1 ×I2 көбейтіндісімен беріледі (4в-сурет). Суреттен бір саңылаудан алынатын дифракциялық суреттің орталық максимумы аймағына
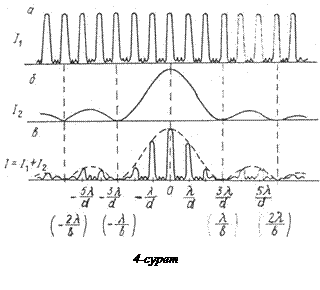
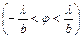түсетін бас максимумдардың ғана интенсивтігі жоғары болатындығы көрінеді. Осындай максимумдар саны тордың d тұрақтысы мен b саңылау ені арасындағы қатынасқа тәуелді болады. Шынында да I2 қисықтың бірінші минимумы (j бұрышының оң мәндері жағына қарай) (4) бойынша 
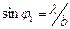теңдігімен анықталатын j=j1 жағдайында жатады. j1 бұрышының осы мәніне, егер 
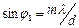шарты орындалатын болса, мұндағы m бүтін сан болуы тиіс, I1 қисығының бас максимумы келеді. Осы теңдіктерді салыстырудан
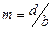(5)
болатынын табамыз.
Сонымен, егер тордың тұрақтысының саңылау еніне қатынасы бүтін сан болса, онда реті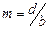 
болатын бас максимум I2 қисығының минимумына түседі де, жойылады. Реттері 
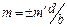, мұндағы m¢= 1, 2,…, болатын барлық бас максимумдар үшін де осы жағдай орындатындығына оңай көз жеткізуге болады. I2 қисығының орталық максимумының аумағына I1 қисығының ( 
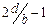) бас максимумдары түседі. I1 қисығының қалған барлық максимумдары I2 қисығының екінші реттік максимумдарына келеді. 4-суретте бірдей қашықтықтарда тұрған төрт саңылау және 
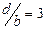. d=а+b болатындықтан, d=3b теңдігінен саңылаулар арасындағы мөлдір емес аралықтар саңлаулардың өздерінен 2 есе кең (а=2b) болады.
Дата добавления: 2015-11-04; просмотров: 2870;