Максвелл ввел понятие полного тока,равного сумме токов проводимости (а также конвекционных токов) и смещения.Плотность полного тока 19 страница

Зная функцию распределения f(q, р), можно решить основную задачу квантовой статистики — определить средние значения величин, характеризующих рассматрива­емую систему. Среднее значение любой функции

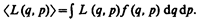(234.2)

Если иметь дело не с координатами и импульсами, а с энергией, которая квантует­ся, то состояние системы характеризуется не непрерывной, а дискретной функцией распределения.

Явное выражение функции распределения в самом общем виде получил американс­кий физик Д. Гиббс (1839—1903). Оно называетсяканоническим распределением Гиббса.В квантовой статистике каноническое распределение Гиббса имеет вид

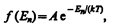(234.3)

где А — постоянная, определяемая из условия нормировки к единице, n — совокуп­ность всех квантовых чисел, характеризующих данное состояние. Подчеркнем, что f(Е_n) есть именно вероятность данного состояния, а не вероятность того, что система имеет определенное значение энергии Е_n, таккак данной энергии может соответ­ствовать не одно, а несколько различных состояний (может иметь место вырождение).

§ 235. Понятие о квантовой статистике Бозе — Эйнштейна и Ферми — Дирака

Одним из важнейших «объектов» изучения квантовой статистики, как и классической, является идеальный газ. Это связано с тем, что во многих случаях реальную систему можно в хорошем приближении считать идеальным газом. Состояние системы невза­имодействующих частиц задается с помощью так называемых чисел заполнения N_i — чисел, указывающих степень заполнения квантового состояния (характеризуется данным набором i квантовых чисел) частицами системы, состоящей из многих тождест­венных частиц. Для систем частиц, образованных бозонами — частицами с нулевым или целым спином (см. § 226), числа заполнения могут принимать любые целые значения: 0, 1, 2, ... (см. § 227). Для систем частиц, образованных фермионами — частицами с полуцелым спином (см. § 226), числа заполнения могут принимать лишь два значения: 0 для свободных состояний и 1 для занятых (см. § 227). Сумма всех чисел заполнения должна быть равна числу частиц системы. Квантовая статистика позволяет подсчитать среднее число частиц в данном квантовом состоянии, т. е. определить средние числа заполнения áN_iñ.

Идеальный газ из бозонов —бозе-газ — описываетсяквантовой статистикой Бозе — Эйнштейна.* Распределение бозонов по энергиям вытекает из так называемого большого канонического распределения Гиббса (с переменным числом частиц) при условии, что число тождественных бозонов в данном квантовом состоянии может быть любым (см. § 227):

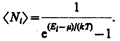(235.1)

* Ш. Бозе (1894—1974) — индийский физик.

Это распределение называетсяраспределением Бозе — Эйнштейна. Здесь áN_iñ — сред­нее число бозонов в квантовом состоянии с энергией E_i, k — постоянная Больцмана, Т—термодинамическая температура, m —химический потенциал; m не зависит от энергии, а определяется только температурой и плотностью числа частиц. Химический потенциал находится обычно из условия, что сумма всех áN_iñ равна полному числу частиц в системе. Здесь m £ 0, так как иначе среднее число частиц в данном квантовом состоянии отрицательно, что не имеет физического смысла. Он определяет изменение внутренней энергии системы при добавлении к ней одной частицы при условии, что все остальные величины, от которых зависит внутренняя энергия (энтропия, объем), фик­сированы.

Идеальный газ из фермионов —ферми-газ — описываетсяквантовой статистикой Ферми — Дирака.* Распределение фермионов по энергиям имеет вид

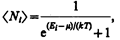(235.2)

где áN_iñ — среднее число фермионов в квантовом состоянии с энергией Е_i, m — хи­мический потенциал. В отличие от (235.1) m может иметь положительное значение (это не приводит к отрицательным значениям чисел áN_iñ). Это распределение называется распределением Ферми — Дирака.

* Э. Ферми (1901—1954) — итальянский физик.

Если 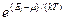>>1, то распределения Бозе — Эйнштейна (235.1) и Ферми — Дирака (235.2) переходят в классическое распределение Максвелла — Больцмана:

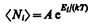(235.3)

(ср. с выражением (44.4)), где

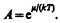(235.4)

Таким образом, при высоких температурах оба «квантовых» газа ведут себя подобно классическому газу.

Система частиц называетсявырожденной, если ее свойства существенным образом отличаются от свойств систем, подчиняющихся классической статистике. Поведение как бозе-газа, так и ферми-газа отличается от классического газа, они являются вырожденными газами. Вырождение газов становится существенным при весьма низ­ких температурах и больших плотностях.Параметром вырождения называется вели­чина А. При А<<1,т. е. при малой степени вырождения, распределения Бозе — Эйнш­тейна (235.1) и Ферми — Дирака (235.2) переходят в классическое распределение Макс­велла — Больцмана (235.3).

Температурой вырождения Т₀ называется температура, ниже которой отчетливо проявляются квантовые свойства идеального газа, обусловленные тождественностью частиц, т. е. Т₀ — температура, при которой вырождение становится существенным. Если Т >> Т₀, то поведение системы частиц (газа) описывается классическими за­конами.

§ 236. Вырожденный электронный газ в металлах

Распределение электронов по различным квантовым состояниям подчиняется принци­пу Паули (см. § 227), согласно которому в одном состоянии не может быть двух одинаковых (с одинаковым набором четырех квантовых чисел) электронов, они долж­ны отличаться какой-то характеристикой, например направлением спина. Следователь­но, по квантовой теории, электроны в металле не могут располагаться на самом низшем энергетическом уровне даже при 0 К. Согласно принципу Паули, электроны вынуждены взбираться вверх «по энергетической лестнице».

Электроны проводимости в металле можно рассматривать как идеальный газ, подчиняющийся распределению Ферми — Дирака (235.2). Если m₀ — химический поте­нциал электронного газа при Т=0 К, то, согласно (235.2), среднее число áN(E)ñ электронов в квантовом состоянии с энергией Е равно

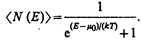(236.1)

Для фермионов (электроны являются фермионами) среднее число частиц в квантовом состоянии и вероятность заселенности квантового состояния совпадают, так как кван­товое состояние либо может быть не заселено, либо в нем будет находиться одна частица. Это означает, что для фермионов áN(E)ñ =f(E), где f(E) — функция рас­пределения электронов по состояниям.

Из (236.1) следует, что при T=0 К функция распределения áN(E)ñ = 1, если E<m₀, и áN(E)ñ = 0, если Е>m₀. График этой функции приведен на рис. 312, а. В области энергий от 0 до m₀ функция áN(E)ñ равна единице. При E=m₀ она скачкообразно изменяется до нуля. Это означает, что при Т=0К все нижние квантовые состояния, вплоть до состояния с энергией E=m₀, заполнены электронами, а все состояния с энергией, большей m₀, свободны. Следовательно, m₀ есть не что иное, как максималь­ная кинетическая энергия, которую могут иметь электроны проводимости в металле при 0 К. Эта максимальная кинетическая энергия называетсяэнергией Ферми и обозна­чается Е_F (Е_F=m₀). Поэтому распределение Ферми — Дирака обычно записывается в виде

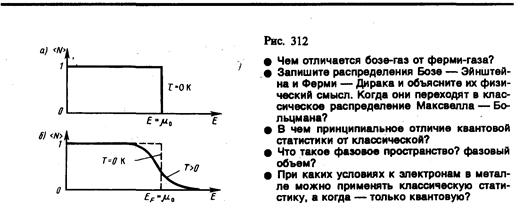
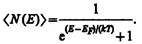(236.2)

Наивысший энергетический уровень, занятый электронами, называетсяуровнем Ферми. Уровню Ферми соответствует энергия Ферми Е_F, которую имеют электроны на этом уровне. Уровень Ферми, очевидно, будет тем выше, чем больше плотность электронного газа. Работу выхода электрона из металла нужно отсчитывать не от дна «потенциальной ямы», как это делалось в классической теории, а от уровня Ферми, т. е. от верхнего из занятых электронами энергетических уровней.

Для металлов при не слишком высоких температурах выполняется неравенство kT<<E_F. Это означает, что электронный газ в металлах практически всегда находится в состоянии сильного вырождения. Температура Т₀ вырождения (см. § 235) находится из условия kT₀=E_F. Она определяет границу, выше которой квантовые эффекты перестают быть существенными. Соответствующие расчеты показывают, что для электронов в металле T₀»10⁴ К, т. с. для всех температур, при которых металл может существовать в твердом состоянии, электронный газ в металле вырожден.

При температурах, отличных от 0 К, функция распределения Ферми — Дирака (236.2) плавно изменяется от 1 до 0 в узкой области (порядка kT) в окрестности Е_F (рис. 312, б). (Здесь же для сравнения пунктиром приведена функция распределения при T=0 К.) Это объясняется тем, что при T>0 небольшое число электронов с энергией, близкой к Е_F, возбуждается вследствие теплового движения и их энергия становится больше Е_F. Вблизи границы Ферми при Е< Е_F заполнение электронами меньше еди­ницы, а при Е> Е_F — больше нуля. В тепловом движении участвует лишь небольшое число электронов, например при комнатной температуре Т»300 К и температуре вырождения T₀=3×10⁴ К, — это 10^–5 от общего числа электронов.

Если (Е–Е_F)>>kТ («хвост» функции распределения), то единицей в знаменателе (236.2) можно пренебречь по сравнению с экспонентой и тогда распределение Фер­ми — Дирака переходит в распределение Максвелла — Больцмана. Таким образом, при (Е–Е_F)>>kT, т.е. при больших значениях энергии, к электронам в металле применима классическая статистика, в то же время, когда (Е–Е_F)<<kT, к ним примени­ма только квантовая статистика Ферми — Дирака.

§ 237. Понятие о квантовой теории теплоемкости. Фононы

Квантовая статистика устранила трудности в объяснении зависимости теплоемкости газов (в частности, двухатомных) от температуры (см. § 53). Согласно квантовой механике, энергия вращательного движения молекул и энергия колебаний атомов в молекуле могут принимать лишь дискретные значения. Если энергия теплового движения значительно меньше разности энергий соседних уровней энергии (kT<<DE), то при столкновении молекул вращательные и колебательные степени свободы прак­тически не возбуждаются. Поэтому при низких температурах поведение двухатомного газа подобно одноатомному.

Так как разность между соседними вращательными уровнями энергии значительно меньше, чем между колебательными, т. е. DE_вращ<<DE_кол (см. § 230), то с ростом температуры возбуждаются вначале вращательные степени свободы, в результате чего теплоемкость возрастает; при дальнейшем росте температуры возбуждаются и колеба­тельные степени свободы и происходит дальнейший рост теплоемкости (см. рис. 80).

Функции распределения Ферми — Дирака для T=0 К и T>0 заметно различаются (рис. 312) лишь в узкой области энергий (порядка kT). Следовательно, в процессе нагревания металла участвует лишь незначительная часть всех электронов проводимо­сти.Этим и объясняется отсутствие заметной разницы между теплоемкостями метал­лов и диэлектриков, что не могло быть объяснено классической теорией (см. § 103).

Как уже указывалось (см. § 73), классическая теория не смогла объяснить также зависимость теплоемкости твердых тел от температуры, а квантовая статистика реши­ла эту задачу. Так, А. Эйнштейн, приближенно считая, что колебания атомов кристал­лической решетки независимы (модель кристалла как совокупности независимых коле­блющихся с одинаковой частотой гармонических осцилляторов), создал качественную квантовую теорию теплоемкости кристаллической решетки. Она впоследствии была развита П. Дебаем, который учел, что колебания атомов в кристаллической решетке не являются независимыми (рассмотрел непрерывный спектр частот гармонических ос­цилляторов).

Рассматривая непрерывный спектр частот осцилляторов, П. Дебай показал, что основной вклад в среднюю энергию квантового осциллятора вносят колебания низких частот, соответствующих упругим волнам. Поэтому тепловое возбуждение твердого тела можно описать в виде упругих волн, распространяющихся в кристалле. Согласно корпускулярно-волновому дуализму свойств вещества, упругим волнам в кристалле сопоставляютфононы, обладающие энергией Е= 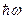. Фонон естьквант энергии звуко­вой волны (так как упругие волны — волны звуковые). Фононы являются квазичасти­цами — элементарными возбуждениями, ведущими себя подобно микрочастицам. Аналогично тому как квантование электромагнитного излучения привело к представлению о фотонах, квантование упругих волн привело к представлению о фононах.

Квазичастицы, в частности фононы, сильно отличаются от обычных частиц (напри­мер, электронов, протонов, фотонов), так как они связаны с коллективным движением многих частиц системы. Квазичастицы не могут возникать в вакууме, они существуют только в кристалле. Импульс фонона обладает своеобразным свойством: при сто­лкновении фононов в кристалле их импульс может дискретными порциями передаваться кристаллической решетке — он при этом не сохраняется. Поэтому в случае фононов говорят о квазиимпульсе.

Энергия кристаллической решетки рассматривается как энергия фононного газа, подчиняющегося статистике Бозе — Эйнштейна (см. § 235), так как фононы являются бозонами (их спин равен нулю). Фононы могут испускаться и поглощаться, но их число не сохраняется постоянным; поэтому в формуле (235.1) для фононов необходимо m положить равным нулю.

Применение статистики Бозе — Эйнштейна к фононному газу — газу из невза­имодействующих бозе-частиц — привело П. Дебая к количественному выводу, соглас­но которому при высоких температурах, когда T>>T_D (классическая область), теплоем­кость твердых тел описывается законом Дюлонга и Пти (см. § 73), а при низких температурах, когда T<<T_D (квантовая область), — пропорциональна кубу термодина­мической температуры: С_V~Т³. 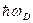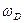В данном случае T_D —характеристическая температу­ра Дебая, определяемая соотношением kТ_D= , где —предельная частота уп­ругих колебаний кристаллической решетки. Таким образом, теория Дебая объяснила расхождение опытных и теоретических (вычисленных на основе классической теории) значений теплоемкости твердых тел (см. § 73 и рис. 113).

Модель квазичастиц — фононов — оказалась эффективной для объяснения откры­того П. Л. Капицей явления сверхтекучести жидкого гелия (см. § 31, 75). Теория сверхтекучести, созданная (1941) Л. Д. Ландау и развитая (1947) российским ученым Н. Н. Боголюбовым (р. 1909), применена впоследствии к явлению сверхпроводимости (см. § 239).

§ 238. Выводы квантовой теории электропроводности металлов

Квантовая теория электропроводности металлов — теория электропроводности, основы­вающаяся на квантовой механике и квантовой статистике Ферми — Дирака, — пере­смотрела вопрос об электропроводности металлов, рассмотренный в классической физике. Расчет электропроводности металлов, выполненный на основе этой теории, приводит к выражению для удельной электрической проводимости металла

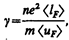(238.1)

которое по внешнему виду напоминает классическую формулу (103.2) для g, но имеет совершенно другое физическое содержание. Здесь п — концентрация электронов прово­димости в металле, ál_Fñ — средняя длина свободного пробега электрона, имеющего энергию Ферми, áu_Fñ — средняя скорость теплового движения такого электрона.

Выводы, получаемые на основе формулы (238.1), полностью соответствуют опытным данным. Квантовая теория электропроводности металлов, в частности, объясняет зависимость удельной проводимости от температуры: g ~ 1/T (классическая теория (см. § 103) дает, что g ~1/ 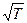), а также аномально большие величины (порядка сотен периодов решетки) средней длины свободного пробега электронов в металле (см. § 103).

Квантовая теория рассматривает движение электронов с учетом их взаимодействия с кристаллической решеткой. Согласно корпускулярно-волновому дуализму, движению электрона сопоставляют волновой процесс. Идеальная кристаллическая решетка (в ее узлах находятся неподвижные частицы и в ней отсутствуют нарушения периодичности) ведет себя подобно оптически однородной среде — она «электронные волны» не рас­сеивает. Это соответствует тому, что металл не оказывает электрическому току — упо­рядоченному движению электронов — никакого сопротивления. «Электронные волны», распространяясь в идеальной кристаллической решетке, как бы огибают узлы решетки и проходят значительные расстояния.

В реальной кристаллической решетке всегда имеются неоднородности, которыми могут быть, например, примеси, вакансии; неоднородности обусловливаются также тепловыми колебаниями. В реальной кристаллической решетке происходит рассеяние «электронных волн» на неоднородностях, что и является причиной электрического сопротивления металлов. Рассеяние «электронных волн» на неоднородностях, связан­ных с тепловыми колебаниями, можно рассматривать как столкновения электронов с фононами.

Согласно классической теории, áuñ ~ 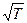, поэтому она не смогла объяснить истин­ную зависимость g от температуры (см. § 103). В квантовой теории средняя скорость áu_Fñ от температуры практически не зависит, так как доказывается, что с изменением температуры уровень Ферми остается практически неизменным. Однако с повышением температуры рассеяние «электронных волн» на тепловых колебаниях решетки (на фононах) возрастает, что соответствует уменьшению средней длины свободного пробе­га электронов. В области комнатных температур ál_Fñ ~Т^–1, поэтому, учитывая незави­симость áuñ от температуры, получим, что сопротивление металлов (R ~ 1/g) в соответ­ствии с данными опытов растет пропорционально Т. Таким образом, квантовая теория электропроводности металлов устранила и эту трудность классической теории.

§ 239. Сверхпроводимость. Понятие об эффекте Джозефсона

Преждечем на основе квантовой теории приступить к качественному объяснению явления сверхпроводимости, рассмотрим некоторые свойства сверхпроводников.

Различные опыты, поставленные с целью изучения свойств сверхпроводников, приводят к выводу, что при переходе металла в сверхпроводящее состояние не изменя­ется структура его кристаллической решетки, не изменяются его механические и оп­тические (в видимой и инфракрасной областях) свойства. Однако при таком переходе наряду со скачкообразным изменением электрических свойств качественно меняются его магнитные и тепловые свойства. Так, в отсутствие магнитного поля переход в сверхпроводящее состояние сопровождается скачкообразным изменением теплоем­кости, а при переходе в сверхпроводящее состояние во внешнем магнитном поле скачком изменяются и теплопроводность, и теплоемкость (такие явления характерны для фазовых переходов II рода; см. § 75). Достаточно сильное магнитное поле (а следовательно, и сильный электрический ток, протекающий по сверхпроводнику) раз­рушает сверхпроводящее состояние.

Как показал немецкий физик В. Мейсснер (1882—1974), в сверхпроводящем состоя­нии магнитное поле в толще сверхпроводника отсутствует. Это означает, что при охлаждении сверхпроводника ниже критической температуры (см. § 98) магнитное поле из него вытесняется(эффект Мейсснера).

Общность эффектов, наблюдаемых в сверхпроводящем состоянии различных ме­таллов, их соединений и сплавов, указывает на то, что явление сверхпроводимости обусловлено физическими причинами, общими для различных веществ, т. е. должен существовать единый для всех сверхпроводников механизм этого явления.

Физическая природа сверхпроводимости была понята лишь в 1957 г. на основе теории (создана Ландау в 1941 г.) сверхтекучести гелия (см. § 237). Теория сверх­проводимости создана американскими физиками Д. Бардином (р. 1908), Л. Купером (р. 1930) и Д. Шриффером (р. 1931) и развита Н. Н. Боголюбовым.

Оказалось, что помимо внешнего сходства между сверхтекучестью (сверхтекучая жидкость протекает по узким капиллярам без трения, т. е. без сопротивления течению) и сверхпроводимостью (ток в сверхпроводнике течет без сопротивления по проводу) существует глубокая физическая аналогия: и сверхтекучесть, и сверхпроводи­мость — этомакроскопический квантовый эффект.

Качественно явление сверхпроводимости можно объяснить так. Между электрона­ми металла помимо кулоновского отталкивания, в достаточной степени ослабляемого экранирующим действием положительных ионов решетки, в результате электрон-фононного взаимодействия (взаимодействия электронов с колебаниями решетки) воз­никает слабое взаимное притяжение. Это взаимное притяжение при определенных условиях может преобладать над отталкиванием. В результате электроны проводимо­сти, притягиваясь, образуют своеобразное связанное состояние, называемоекуперовской парой. «Размеры» пары много больше (примерно на четыре порядка) среднего межатомного расстояния, т. е. между электронами, «связанными» в пару, находится много «обычных» электронов.

Чтобы куперовскую пару разрушить (оторвать один из ее электронов), надо затратить некоторую энергию, которая пойдет на преодоление сил притяжения элект­ронов пары. Такая энергия может быть в принципе получена в результате взаимодейст­вия с фононами. Однако пары сопротивляются своему разрушению. Это объясняется тем, что существует не одна пара, а целый ансамбль взаимодействующих друг с другом куперовских пар.

Электроны, входящие в куперовскую пару, имеют противоположно направленные спины. Поэтому спин такой пары равен нулю и она представляет собой бозон. К бозонам принцип Паули неприменим, и число бозе-частиц, находящихся в одном состоянии, не ограничено. Поэтому при сверхнизких температурах бозоны скапливают­ся в основном состоянии, из которого их довольно трудно перевести в возбужденное. Система бозе-частиц — куперовских пар, обладая устойчивостью относительно воз­можности отрыва электрона, может под действием внешнего электрического поля двигаться без сопротивления со стороны проводника, что и приводит к сверхпроводи­мости.

На основе теории сверхпроводимости английский физик Б. Джозефсон (р. 1940) в 1962 г. предсказал эффект, названный его именем (Нобелевская премия 1973 г.). Эффект Джозефсона (обнаружен в 1963 г.) — протекание сверхпроводящего тока сквозь тонкий слой диэлектрика (пленка оксида металла толщиной »1 нм), раз­деляющий два сверхпроводника (так называемыйконтакт Джозефсона). Электроны проводимости проходят сквозь диэлектрик благодаря туннельному эффекту. Если ток через контакт Джозефсона не превышает некоторое критическое значение, то падения напряжения на нем нет(стационарный эффект), если превышает — возникает падение напряжения U и контакт излучает электромагнитные волны(нестационарным эффект).Частота n излучения связана с U на контакте соотношением n=2eU/h (е — заряд электрона). Возникновение излучения объясняется тем, что куперовские пары (они создают сверхпроводящий ток), проходя сквозь контакт, приобретают относительно основного состояния сверхпроводника избыточную энергию. Возвращаясь в основное состояние, они излучают квант электромагнитной энергии hn=2eU.

Эффект Джозефсона используется для точного измерения очень слабых магнитных полей (до 10^–18 Тл), токов (до 10^–10 А) и напряжений (до 10^–15 В), а также для создания быстродействующих элементов логических устройств ЭВМ и усилителей.

Глава 31 Элементы физики твердого тела

§ 240. Понятие о зонной теории твердых тел

Используя уравнение Шредингера — основное уравнение динамики в нерелятивистской квантовой механике, — в принципе можно рассмотреть задачу о кристалле, например найти возможные значения его энергии, а также соответствующие энергетические состояния. Однако как в классической, так и в квантовой механике отсутствуют методы точного решения динамической задачи для системы многих частиц. Поэтому эта задача решается приближенно сведением задачи многих частиц к одноэлектронной задаче об одном электроне, движущемся в заданном внешнем поле. Подобный путь приводит к зонной теории твердого тела.

В основе зонной теории лежит так называемое адиабатическоеприближение. Квантово-механическая система разделяется на тяжелые и легкие частицы — ядра и элект­роны. Поскольку массы и скорости этих частиц значительно различаются, можно считать, что движение электронов происходит в поле неподвижных ядер, а медленно движущиеся ядра находятся в усредненном поле всех электронов. Принимая, что ядра в узлах кристаллической решетки неподвижны, движение электрона рассматривается в постоянном периодическом поле ядер.

Далее используется приближение самосогласованного поля. Взаимодействие дан­ного электрона со всеми другими электронами заменяется действием на него стаци­онарного электрического поля, обладающего периодичностью кристаллической решет­ки. Это поле создается усредненным в пространстве зарядом всех других электронов и всех ядер. Таким образом, в рамках зонной теории многоэлектронная задача сводится к задаче о движении одного электрона во внешнем периодическом по­ле — усредненном и согласованном поле всех ядер и электронов.

Рассмотрим мысленно «процесс образования» твердого тела из изолированных атомов. Пока атомы изолированы, т. е. находятся друг от друга на макроскопических расстояниях, они имеют совпадающие схемы энергетических уровней (рис. 313). По мере «сжатия» нашей модели до кристаллической решетки, т. е. когда расстояния между атомами станут равными межатомным расстояниям в твердых телах, взаимо­действие между атомами приводит к тому, что энергетические уровни атомов смеща­ются, расщепляются и расширяются в зоны, образуетсязонный энергетический спектр.

Из рис. 313, на котором показано расщепление энергетических уровней в зависимо­сти от расстояния r между атомами, видно, что заметно расщепляются и расширяются лишь уровни внешних, валентных электронов, наиболее слабо связанных с ядром и имеющих наибольшую энергию, а также более высокие уровни, которые в основном состоянии атома вообще электронами не заняты. Уровни же внутренних электронов либо совсем не расщепляются, либо расщепляются слабо. Таким образом, в твердых телах внутренние электроны ведут себя так же,как в изолированных атомах, валентные же электроны «коллективизированы» — принадлежат всему твердому телу.

Образование зонного энергетического спектра в кристалле является квантово-механическим эффектом в вытекает из соотношения неопределенностей. В кристалле ва­лентные электроны атомов, связанные слабее с ядрами,чем внутренние электроны, могут переходить от атома к атому сквозь потенциальные барьеры, разделяющие атомы, т. е. перемещаться без изменений полной энергии (туннельный эффект, см. § 221). Это приводит к тому, что среднее время жизни t валентного электрона в данном атоме по сравнению с изолированным атомом существенно уменьшается и составляет примерно 10^–15 с (для изолированного атома оно примерно 10^–8 с). Время же жизни электрона в каком-либо состоянии связано с неопределенностью его энергии (шириной уровня) соотношением неопределенностей DE~h/t (см. (215.5)). Следовательно, если естественная ширина спектральных линий составляет примерно 10^–7 эВ, то в кристал­лах DE»1¸10 эВ, т. е. энергетические уровни валентных электронов расширяются в зону дозволенных значений энергии.