Кинематическая цепь

Связанная система звеньев, образующих между собой кинематические пары, называется кинематической цепью.

Кинематические цепи по характеру относительного движения звеньев разделяются на плоские и пространственные.

Кинематическая цепь называется тоской, если точки звеньев описывают траектории, лежащие в параллельных плоскостях. Кинематическая цепь называется пространственной, если точки ее звеньев описывают неплоские

траектории или траектории, лежащие в пересекающихся плоскостях. Наи­большее распространение на практике имеют плоские кинематические цепи.

По виду звеньев, входящих в кинематические цепи, последние разделя­ются на простые и сложные.

Простой кинематической цепью называется такая цепь, в которой каж­дое звено участвует в образовании не более двух кинематических пар (рис. 1.3, а).

Сложной кинематической цепью называется цепь, в которой имеется хотя бы одно звено, входящее более чем в две кинематические пары (рис. 1.3, б).

Все кинематические цепи, кроме того, подразделяются на незамкнутые и замкнутые.

Незамкнутыми кинематическими цепями называют такие цепи, в которых имеются звенья, образующие только одну кинематическую пару (см. рис. 1.3, а, б).

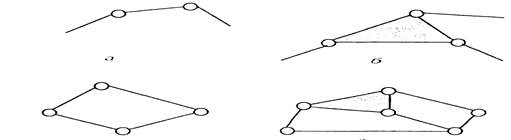
Рис. 1.3

Замкнутыми называ­ются кинематические цепи, в которых каждое звенообразует не менее чем две кинематические пары (рис. 1.3, в, г).

H = 3k – 2p1 – p2 (1.1)

В технике обычно интересует движение звеньев кинематической цепи относительно одного из звеньев, которое является неподвижным и называется стойкой. Если одно звено кинематической цепи сделать неподвижным, то число степеней свободы уменьшится еще на три и относительно неподвижно­го звена (стойки) будет равно

W = H – 3 = 3(k–1) – 2p1 – p2 (1.2)

где W – число степеней свободы кинематической цени относительно неподвижного звена.

Обозначив к-1= п (количество подвижных звеньев кинематической цепи), окончательно получим выражение для числа степеней свободы кине­матической пени относительно неподвижного звена

W = 3n – 2p1 – p2 (1.3)

Число степеней свободы кинематической цепи IV относительно непод­вижного звена (стойки) называется степенью подвижности кинематической цепи. Формула (1.3) впервые была получена русским ученым П. Л. Чебышевым и носит его имя. Следует отметить, что эта формула пригодна только для определения степени подвижности плоских кинематических цепей.

Механизмы

Дадим определение механизма на основании понятия о кинематической цепи. Предварительно отметим, что звенья кинематической цепи, законы движения которых являются заданными, называются ведущими, остальные звенья называются ведомыми.

Механизмом называется кинематическая цепь с одним неподвижным звеном (стопкой), в которой при заданном законе движения одного или нескольких ведущих звеньев все остальные (ведомые) звенья движутся вполне определенным образом.

Рассмотрим условия, при которых кинематическая цепь будет механиз­мом. Известно, что точка на плоскости имеет две степени свободы и для оп­ределения ее положения необходимо задать две координаты. В случае твер­дого тела, имеющего при плоском движении три степени свободы, для одно­значного определения его положения необходимо знать три координаты: две координаты точки, выбранной за полюс, и угол поворота некоторого отрезка, соединяющего две точки тела.

Аналогично и для кинематической цепи. Чтобы положения всех звень­ев кинематической цепи относительно стойки были вполне определенными, необходимо задать столько параметров, сколько степеней подвижности (степеней свободы относительно стойки) имеет кинематическая цепь. Параметры, которые задаются кинематической цепи, определяются заданным законом движения ведущего звена (или ведущих звеньев). Поэтому, чтобы движения ведомых звеньев кинематической цепи были вполне определенными, необходимо, чтобы количество ведущих звеньев цепи было равно степени подвижности этой цепи. Только в этом случае кинематическая цепь является механизмом.

На рис. 1.4 изображены замкнутые кинематические цепи разной степени подвижности. Кинематическая цепь на рис. 1.4, а представляет собой неподвижное соединение звеньев (W = 0) и не может быть механизмом. Остальные кинематические цепи (рис. 1.4. б - ж) при определенных условиях могут быть механизмами. Так кинематическая цепь на рис. 1.4. д. станет механиз­мом, если будет задан закон движения двух ведущих звеньев (W = 2). Осталь­ные кинематические цепи являются механизмами, если известен закон дви­жения одного из звеньев цепи (W = 1). Для механизма, представленного на рис. 1.4. .ж, степень подвижности на единицу больше по сравнению с аналогичным механизмом, представленным на рис. 1.4, е. Увеличение степени под­вижности механизма вызвано введением дополнительно подвижного звена – ролика с целью замены трения скольжения на трение качения.

В 1916 г. профессором Петербургского политехнического института Л. В. Ассуром был предложен следующий принцип образования механизмов: любой механизм может быть образован путем непосредственного присоединения («наслоения») сначала к ведущему звену и стойке, а затем и к любым другим звеньям кинематических цепей с нулевой степенью подвижности.

В самом деле, присоединение к ведущему звену кинематических цепей с путевой степенью подвижности (W = 0) не изменит общей степени подвиж­ности механизма.

Кинематические цепи, обладающие нулевой степенью подвижности (степенью свободы относительно стойки), называются группами Аcсура. Все разнообразие групп Аcсура можно получить из формулы Чебышева.

Будем полагать, что кинематическая цепь состоит лишь из пар 1-го класса. Тогда для группы Аcсура с нулевой степенью подвижности (W = 0) получим

W = 3n – 2p1 = 0 (1.4)

или

P1 = (3/2)*n (1.5)

Так как количество звеньев и кинематических пар может быть только целым числом, то количество звеньев группы Ассура может быть только четным числом. Следовательно, равенству (1.5) могут удовлетворять следующие числа подвижных звеньев п и кинематических пар 1-го класса р1.

n = 2,4,6……

p1 = 3,6,9 …..

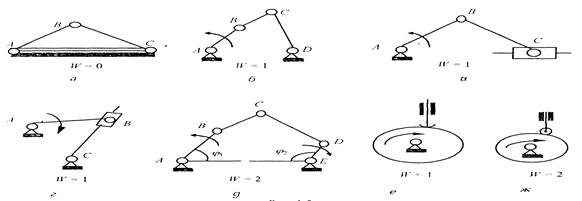
Рис. 1.4

В зависимости от количества звеньев и числа кинематических пар опре­деляется класс группы Ассура. Так, кинематическая цепь с количеством звеньев п = 2 и количеством кинематических пар р1 = 3 является группой Ассура 1-го класса. При п = 2 и р₁ = 3 будем иметь группу Ассура 2-го класса и т. д.

Примеры групп Ассура 1-го и 2-го классов представлены на рис. 1.5, а, 6.

Если присоединить любую группу Ассура к стойке, то получим кинематическую цепь с нулевой степенью подвижности, т. е. ферму (рис. 1.6, а), а если присоединить ее внешними кинематическими парами к ведущему звену и к стойке или к новым звеньям первоначального механизма, то получим новый механизм, степень подвижности которого не изменится (рис. 1.6, б).

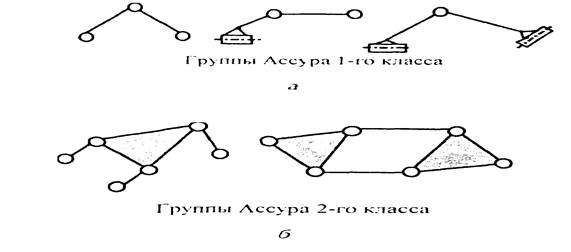
Рис 1.5

В соответствии со строе­нием механизмы делятся на классы. Класс механизма за­висит от классов групп Ас­сура, входящих в его состав. Если в состав механизма входят группы Ассура раз­личных классов, то номер класса механизма определя­ется номером класса наи­высшей группы Ассура. На рис. 1.6. б изображен меха­низм, в состав которого входят группы Ассура 1-го и 2-го классов. Исходя из сказан­ного выше, данный меха­низм является механизмом 2-го класса.

Механизмы, не содержащие групп Ассура, а состоящие только из ведущего звена, относятся к механизмам нулевого класса. Такие механизмы встречаются на практике довольно часто. К ним, например, относятся механизмы электродвигателей, генераторов и так далее.

Рассмотренная классификация механизмов не является единственной. Существуют также другие виды классификаций. Широко ис­пользуется практическая классификация механизмов, ко­торая в общих чертах учитывает основные кинематические свойства и конст­руктивные особенности механизмов, а в отдельных случаях и функциональ­ное назначение.

В соответствии с практической классификацией механизмы делятся на следующие виды:

а) зубчатые передачи;

б) фрикционные передачи;

в) передачи с гибкой связью;

г) винтовые механизмы;

д) кулачковые механизмы;

е) рычажные механизмы;

ж)механизмы прерывистого действия;

з)электромагнитный механизмы и др.

На рис. 1.7 представлены кинематические схемы механизмов в соответствии с практической классификацией:

фрикционные механизмы: цилиндрический (а) и конический с постоянным передаточным отношением (б), с переменным передаточным отношением (в):

кулачковые механизмы: с поступательно движущимся (г) и качающимся (д) толка гелем;

механизм с гибкой связью (е)

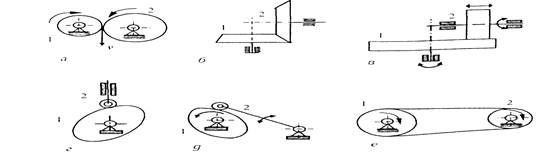
Рис 1.6