Положение прямой относительно плоскостей проекций. Следы прямой.

В зависимости от положения прямой по отношению к плоскостям проекций она может занимать как общее, так и частные положения.

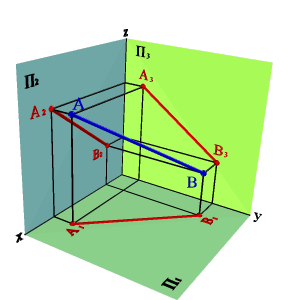
1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения (рис.3.4).

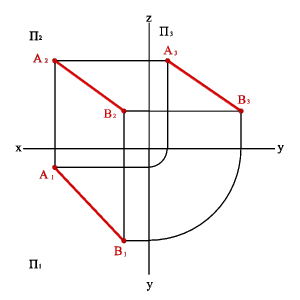
а) модель	б) эпюр
Рисунок 3.4. Прямая общего положения

2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:

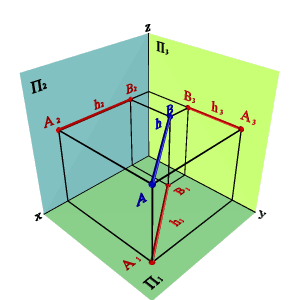
2.1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями (рис.3.5). Для любой пары точек горизонтали должно быть справедливо равенство

z_A=z_B Þ A₂B₂//0x; A₃B₃//0y Þ x_Ax–_B,# y_Ay–_B,# z_Az–_B.=

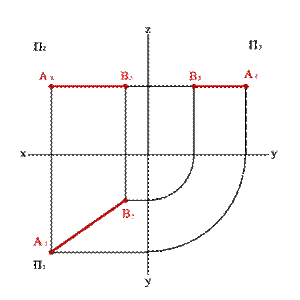
а) модель	б) эпюр
Рисунок 3.5. Горизонтальная прямая //

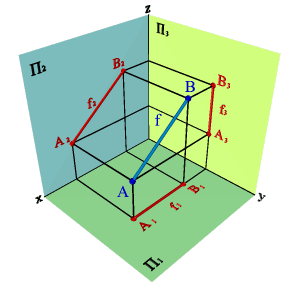
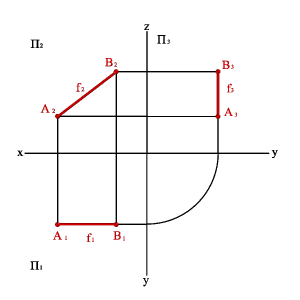
2.2. Прямые параллельные фронтальной плоскости проекций называютсяфронтальнымиили фронталями(рис.3.6).

y_Ay=_BÞ A₁B₁,x A₃B₃z Þ x_Ax–_B,# y_Ay–_B,= z_Az–_B.#

а) модель	б) эпюр
Рисунок 3.6. Фронтальная прямая

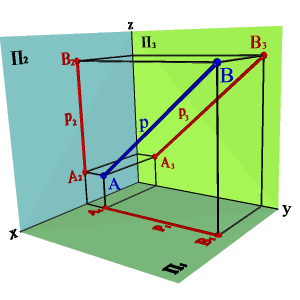
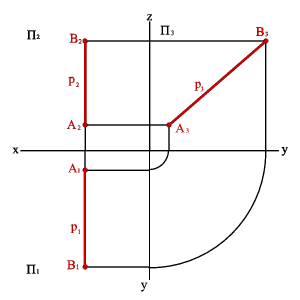
2.3. Прямые параллельные профильной плоскости проекций называются профильными (рис. 3.7).

x_A=x_BÞ A₁B₁,y A₂B₂z Þ x_Ax–_B,= y_Ay–_B,# z_Az–_B.#

Различают восходящую и нисходящуюпрофильные прямые. Первая по мере удаления от зрителя поднимается, вторая - понижается.

а) модель	б) эпюр
Рисунок 3.7. Профильная прямая

3. Прямые перпендикулярные плоскостям проекций, называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим. В зависимости от того, какой плоскости проекций перпендикулярна исследуемая прямая, различают:

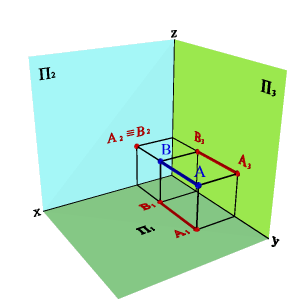
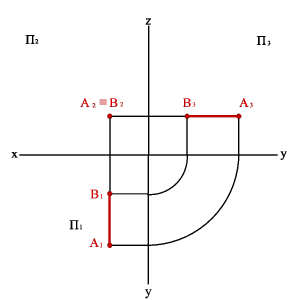
3.1. Фронтально проецирующая прямая - АВ.сир( 8.3)

x_Ax–_B=ü

y_Ay–_B#ý

z_Az–_B=þ,

а) модель	б) эпюр
Рисунок 3.8. Фронтально проецирующая прямая

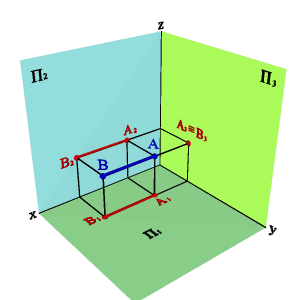
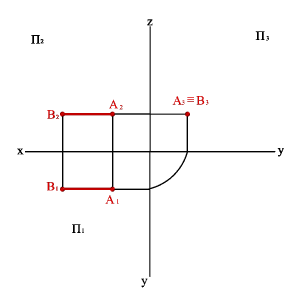
3.2.Профильно- проецирующая прямая - АВ (рис.3.9)

x_Аx–_B#ü

y_Аy–_B=ý

z_Аz–_B=þ,

а) модель	б) эпюр
Рисунок 3.9. Профильно-проецирующая прямая

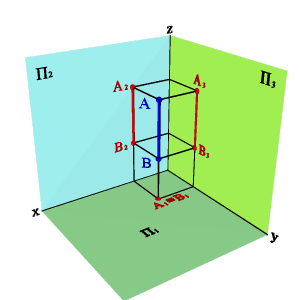
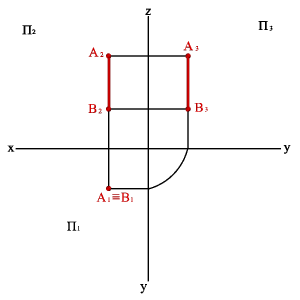
3.3. Горизонтально- проецирующая прямая - АВ (рис.3.10)

x_Аx–_В=ü

y_Аy–_В=ý

ZАz–В#þ.

а) модель	б) эпюр
Рисунок 3.10. Горизонтально-проецирующая прямая

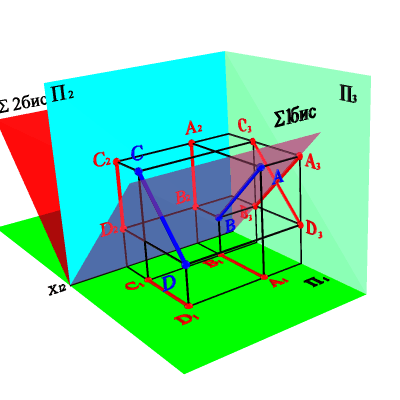
4. Прямые параллельные биссекторным плоскостям (рис. 3.11)

АВ 1Sбис Þ x_Ax–_B=; z_Bz–_Ay=_By–_A; СDS2бис Þ x_Сx–_D=; z_Dz–_Cy=_Cy–_D.

Биссекторной плоскостью называется плоскость проходящая через ось 0х и делящая двухгранный угол между плоскостями проекций П₁ и П₂пополам. Биссекторная плоскость проходящая через 1 и 3 четверти называется первой биссекторной плоскостью (1Sбис) ,а через 2 и 4 четверти - второй (S2бис).

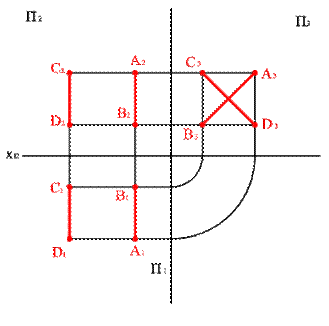
5. Прямые перпендикулярные биссекторным плоскостям (рис. 3.11)

АВS^2бис Þ x_Ax–_B=; z_Bz–_Ay=_Вy–_А;_. СDS^1бис Þ x_Сx–_D=;z_Dz–_Cy=_Cy–_D

а) модель	б) эпюр
Рисунок 3.11. Прямые параллельные и перпендикулярные биссекторным плоскостям

Лекция №3-3

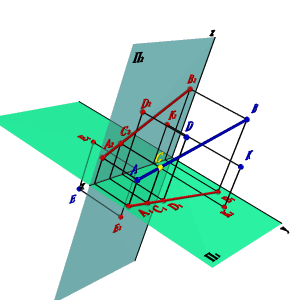
Если точка принадлежит прямой, то её проекции должны принадлежать одноименным проекциям этой прямой (аксиома принадлежности точки прямой). Из четырех предложенных на рисунке 3.14 точек, только одна точка С лежит на прямой АВ.

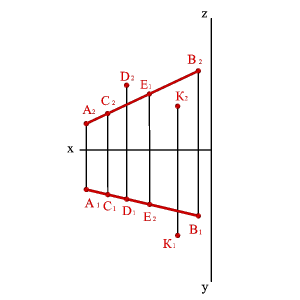
а) эпюр	б) модель
Рисунок 3.14. Взаимное расположение точки и прямой

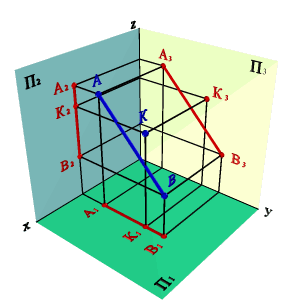
В тех случаях когда точка и прямая лежат в плоскости уровня (параллельной какой-либо из плоскостей проекций П₁, П₂ и П₃), то вопрос о взаимном расположении прямой и точки решается при построении проекций на плоскость соответственно П₁, П₂ или П₃. Например, прямая АВ и точка К лежат в плоскости параллельной профильной плоскости проекций (рис.3.15).

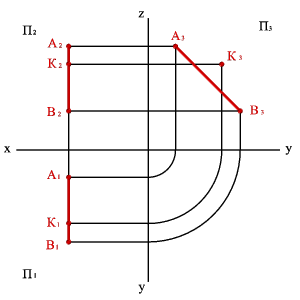
а) эпюр	б) модель
Рисунок 3.15 Точка и прямая, расположенные в профильной плоскости уровня

Лекция № 3-4

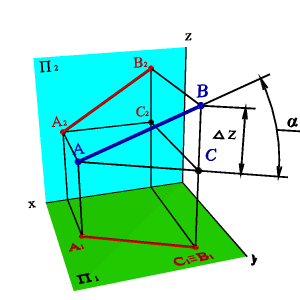
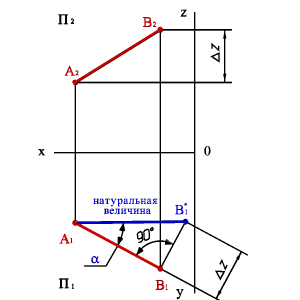
Длину отрезка АВ можно определить из прямоугольного треугольника АВС |AС|=|A₁B₁|, |СB=|ZD, угол a-угол наклона отрезка к плоскости П₁, b-угол наклона отрезка к плоскости П₂. Для этогона эпюре (рис.3.17) из точки B₁ под углом 90⁰ проводим отрезок |B₁B₁* ZD=|,полученныйв результате построений отрезокA₁B₁*и будет натуральной величиной отрезка АВ, а угол B₁A₁B₁* =α. Рассмотренный метод называется методом прямоугольного треугольника. Однако все построения можно объяснить, как вращение треугольникаАВСвокруг стороны AС до тех пор, пока он не станет параллелен плоскости П₁, в этом случае треугольник проецируется на плоскость проекций без искажения. Подробнее вращение вокруг оси параллельной плоскости проекций рассмотрены в разделе «Методы преобразования ортогональных проекций»

а) модель	б) эпюр
Рисунок 3.17. Определение натуральной величины отрезка и угла его наклона к горизонтальной плоскости проекций

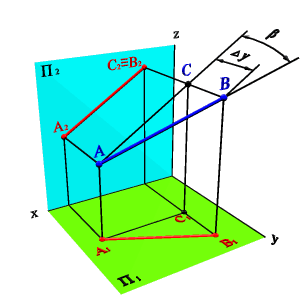
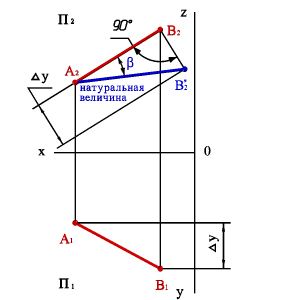
Для определения b-угол наклона отрезка к плоскости П₂ построения аналогичные (рис.3.18). Только в треугольнике АВВ* сторона B|В*=|UDи треугольниксовмещается с плоскостью П₂.

а) модель	б) эпюр
Рисунок 3.18. Определение натуральной величины отрезка и угла его наклона к фронтальной плоскости проекций

Лекция №3-5