Наращенная величина р-срочной ренты
Предположим, что вложение средств и капитализация процентов осуществляются чаще,чем один раз в год.
Пусть 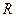 - размер годового платежа;
- размер годового платежа;
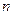 - срок финансовой операции (лет);
- срок финансовой операции (лет);
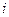 - годовая процентная ставка;
- годовая процентная ставка;
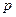 – число платежей в год;
– число платежей в год;
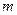 – количество начислений процентов.
– количество начислений процентов.
Тогда платеж за период 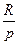
Число процентных периодов 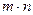 , по ставке
, по ставке  .
.
Наращенные платежи представляют собой геометрическую прогрессию с первым членом 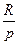 и знаменателем прогрессии
и знаменателем прогрессии 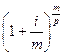 .
.
Количество членов ренты равно р·n. Найдем ее сумму:
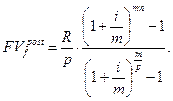 (6.4)
(6.4)
Для ренты пренумерандо: 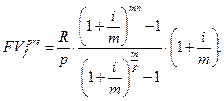 (6.5)
(6.5)
Пример. Страховая компания принимает платежи по полугодиям равными частями по 250 тыс. руб. в течение 3 лет. Банк, обслуживающий компанию, начисляет проценты ежеквартально из расчета 10% годовых. Определить, какую сумму получит страховая компания по истечению срока договора.
Решение: 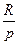 =250 тыс. руб.,
=250 тыс. руб., 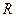 =500 тыс. руб.; i=0,1; p=2 раза; m=4 раза; n=3 года.
=500 тыс. руб.; i=0,1; p=2 раза; m=4 раза; n=3 года.

Пример. Для обеспечения некоторых будущих расходов создается фонд средств. В фонд поступают платежи в виде постоянной годовой ренты постнумерандо в течение 5 лет. Размер разового платежа 4 млн. руб. На поступившие взносы начисляются проценты по ставке 18,5% годовых.
Найти величину фонда на конец срока, если
1). Проценты начисляются, и платежи выплачиваются один раз в год.( 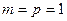 ).
).
R = 4 млн.руб.; i = 18,5% годовых; n=5 лет.
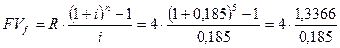 =28,90 млн. руб.
=28,90 млн. руб.
2). Проценты начисляются поквартально, платежи осуществляются один раз в год ( 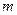 = 4,
= 4, 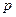 =1),
=1),

Переход от годового начисления процентов к поквартальному несколько увеличил наращенную сумму.
3). Допустим, проценты начисляются раз в год, платежи выплачиваются поквартально. ( 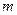 = 1,
= 1, 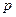 = 4);
= 4);
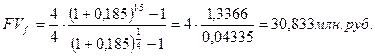
4). Пусть платежи и начисление процентов производятся поквартально. (m = p = 4);
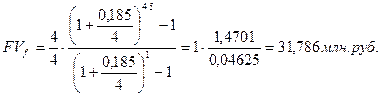
5). Пусть платежи производятся поквартально, а начисление процентов производится ежемесячно ( 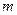 = 12,
= 12, 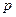 = 4).
= 4).
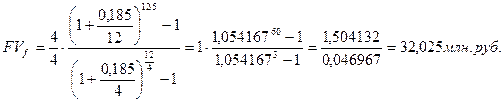
Дата добавления: 2015-10-26; просмотров: 7712;
