Коэффициент запаса усталостной прочности и его определение

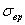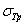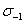Построим диаграмму усталостной прочности и нанесем на ней рабочую точку цикла. Диаграмма строится, как это было показано выше, на основе заданных механических характеристик материала , и , а рабочая точка определяется по номинальным значениям напряжений цикла 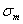и 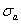. С учетом поправки на концентрацию напряжений, на поверхностный и масштабный факторы координаты рабочей точки примут значения 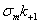и 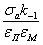(рис. 9).

Условимся под запасом усталостной прочности понимать отношение отрезка ОВ к отрезку ОА (см. рис. 9)

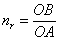
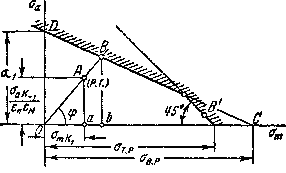
Рис.9. Диаграмма усталостной прочности.

Это отношение характеризует степень близости рабочих условий к предельным для данного материала. В частном случае, когда напряжения не меняются во времени ( 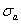= 0), данное определение запаса прочности совпадает с обычным.

При подсчете запаса прочности можно прибегать к графическому построению диаграммы усталостной прочности и глазомерной оценке соотношения между отрезками. Точность такого определения остается в пределах точности определения исходных величин и последующих поправок.

В большинстве случаев для определения n предпочитают пользоваться расчетными формулами. Они получаются из геометрических соотношений отрезков, показанных на рис. 9.

Уравнения прямых СD и ОB будут:

,

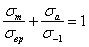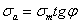
Исключая из этих уравнений 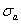, находим абсциссу точки B, те.— отрезок Оb,

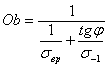
Искомый запас усталостной прочности:

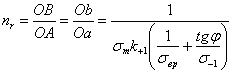
Так как:

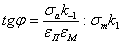
то

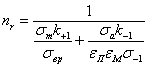
Если точка В находится на прямой, ограничивающей цикл по пределу текучести (точка В' на диаграмме рис. 9), расчет на усталостную прочность заменяется обычным расчетом по пределу текучести.

Все рассмотренные до сих пор вопросы усталостной прочности относились к случаю одноосного напряженного состояния. Совершенно аналогичным образом могут быть получены соотношения усталостной прочности для чистого сдвига (кручения). В случаях более общего напряженного состояния задача существенно усложняется.

Известны многие попытки создания гипотез усталостной прочности в сложном напряженном состоянии. Все они сводились в основном к обобщению известных гипотез предельных состояний на случай циклических напряжений. Такой путь, однако, до сих пор не дал положительных результатов, и в настоящее время приходится пользоваться в основном экспериментально установленными зависимостями.

Для наиболее часто встречающегося на практике расчета при двухосном напряженном состоянии 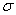, 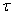общепринятой в настоящее время является эмпирическая формула Гафа и Полларда

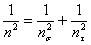
где n — искомый запас усталостной прочности; — запас усталостной прочности в предположении, что касательные напряжения 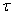отсутствуют; 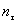— запас по касательным напряжениям, установленный в предположении, что .

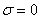Приведенная формула применима не только в случае синфазного изменения 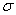и 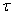, но и при таких циклах, когда максимумы 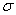и 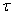достигаются не одновременно.