Расчет бесконечно длинной балки на упругом основании, загруженной одной силой Р.

Расчет балки на упругом основании.

Общие понятия.

К числу статически неопределимых балок может быть отнесена балка на упругом основании. Так называется балка, опирающаяся по всей своей длине (Рис.1) на упругое основание, оказывающее в каждой точке на балку реакцию, пропорциональную у — прогибу балки в этой точке. Коэффициент пропорциональности обозначается буквой k.

Введение предположения о пропорциональности реакций прогибу является приближением, хотя и достаточно близким к действительным условиям.

Рис.1. Расчетная схема балки на упругом основании.

Предложение ввести в расчет коэффициент пропорциональности к, именуемый «коэффициентом постели», было впервые сделано русским академиком Николаем Ивановичем Фуссом в 1801 году. Принимая это предположение, получаем, что интенсивность реакции основания в каждой точке сила равна ky и измеряется в единицах силы и длины; размерность коэффициента k при этом будет сила и квадрат длины. Будем считать, что основание оказывает реакцию при прогибах балки как вниз, так и вверх.

На практике задачи о расчете балки на упругом основании встречаются в железнодорожном деле (рельс, шпала), в строительстве — фундаменты различных сооружений, передающие нагрузку на грунт.

Статически неопределимой такая балка будет потому, что условие статики— сумма нагрузок равна всей реакции основания — не дает возможности установить распределение этой реакции по длине балки, а значит, вычислить изгибающие моменты и поперечные силы.

Интенсивность реакции в каждой точке связана с прогибами балки. Поэтому для решения задачи необходимо найти сначала уравнение изогнутой оси , а уже затем формулы для вычисления изгибающего момента и поперечной силы. Ход решения оказывается обратным обычному.

Найдем уравнение изогнутой оси для балки постоянного сечения, лежащей на упругом основании и нагруженной сосредоточенными силами 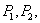... (Рис.1). Начало координат возьмем в любой точке, ось х направим вправо, ось у вертикально вверх. Направление нагрузок вверх будем считать положительным. Напишем обычное дифференциальное уравнение изгиба

Так как М(х) нам неизвестен, то постараемся связать прогибы непосредственно с нагрузкой, для этого дифференцируем дважды предыдущее уравнение:

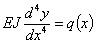
(1)

где q(x)—интенсивность сплошной нагрузки, действующей на балку в сечении с абсциссой х.

Сплошной нагрузкой для нашей балки является лишь реакция упругого основания. Интенсивность ей пропорциональна прогибам; эта нагрузка направлена вверх, т. е. положительна, когда прогибы идут вниз, т. е. отрицательны, и наоборот. Таким образом, эта нагрузка имеет знак, обратный знаку прогибов:

Тогда

	(2)
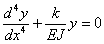
	(3)

Если обозначить , то общий интеграл уравнения (25.3) имеет вид: 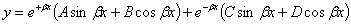(25.4)

Постоянные А, В, С, D должны быть определены в каждом частном случае нагрузки и длины балки. Величина 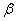имеет измерение обратное длине.

Расчет бесконечно длинной балки на упругом основании, загруженной одной силой Р.

Наиболее просто решается задача об изгибе бесконечно длинной балки, нагруженной одной сосредоточенной силой (Рис.2). Помимо непосредственного практического значения решение этой задачи позволит путем последовательных приближений рассчитывать и балки конечной длины.

Рис.2. Расчетная схема балки бесконечной длины.

Начало координат расположим в точке приложения силы Р. Определим постоянные А, В, С и D. Так как вся реакция основания, равная силе Р должна быть конечной величиной, то прогибы балки в точках, бесконечно удаленных от точки приложения силы, должны обращаться в нуль:

(5)

При бесконечно больших значениях х два вторых слагаемых в правой части формулы (4) обращаются в нуль благодаря множителю 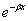, два же первых могут обратиться в нуль лишь пр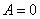и

и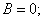

таким образом,

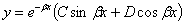
(6)

Далее, по симметрии нагрузки и реакции основания, касательная к изогнутой оси в точке приложения силы должна идти параллельно оси абсцисс:

Дифференцируя (6), получаем:

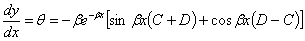
Подставляя в это выражение и приравнивая результат нулю, находим:

D — С = 0 и C=D;

таким образом, уравнения будут:

	(7)
	(8)

Для определения последней постоянной С имеем еще одно уравнение: нам известна величина поперечной силы в начале координат.

Разрезав балку сечением в точке О справа от силы Р и рассматривая правую часть балки, видим, что поперечная сита в этом сечении равна реакции основания, действующей на правую половину балки со знаком минус; так как реакция направлена вверх (для правой половины) и вся реакция основания равна Р, значит, поперечная сила в сечении при х = 0 равна

Но, с другой стороны

(9)

Таким образом,

(10)

Вычисляем, пользуясь (8), и :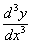

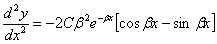
	(11)
	(12)

Подставляя (12) в (10) и приравнивая х нулю, получаем:

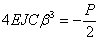и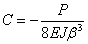

Теперь значения у и ее производных получают вид

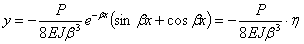
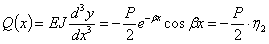
Таким образом, напряженное состояние и деформации балки на упругом основании всецело определяются нагрузкой и коэффициентом 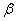, зависящим от соотношения жесткостей балки и упругого основания.