Раздел VIII. Динамические звенья

Тема 15 Типовые динамические звенья

Основные понятия и определения

Любую систему автоматики можно рассматривать с двух точек зрения:

- качественной;

- количественной.

При качественном анализе автоматической системы мы рассматриваем ее как совокупность взаимодействующих между собой функциональных элементов (датчики, усилители, задающее устройство, объект регулирования и т.п.), которые различаются между собой по конструкции и по принципу действия.

Для количественного анализа процессов, происходящих в системе (т.е. математического ее описания), систему разделяют не на функциональные, а на динамические элементы – звенья.

Динамическим звеном называется часть системы, описываемая дифференциальным уравнением определенного вида. Например, зубчатая передача, делитель напряжения – имеют одинаковое математическое описание (формулу работы). Динамическим звеном может быть функциональный элемент, его часть, несколько функциональных элементов или даже вся система автоматики в целом.

В зависимости от характера протекания переходного процесса, различают следующие типовые динамические звенья:

- усилительное;

- дифференцирующее;

- интегрирующее;

- апериодическое;

- колебательное

Усилительным (безинерционным, пропорциональным) звеном называют такое динамическое звено, у которого выходная величина в каждый момент времени пропорциональная входной величине, т.е. выходная величина воспроизводит без искажений и запаздываний входную величину. (Примеры усилительного звена: потенциометр, система рычагов, усилители, зубчатая передача и т.п.)

Дифференцирующим звеном называется такое звено, в котором выходная величина пропорциональна производной во времени входной величине, т.е. выходная величина пропорциональна скорости изменения входной величине. (Примеры дифференцирующего звена: тахометр, спидометр, цепи RC и RL, трансформаторы) .

Интегрирующее звено – такое звено, у которого выходная величина пропорциональна интегралу во времени входной величины. После прекращения действия сигнала на входе, выходной сигнал остается на том же уровне, на котором он был в момент исчезновения входного сигнала, т.е. это звено обладает памятью (Примеры интегрирующего звена: электродвигатель постоянного тока с независимым возбуждением, конденсатор, поршневой гидродвигатель и т.п.)

Апериодическое (инерционное) – звено, в котором при подаче на вход скачкообразного сигнала , выходная величина апериодически (по экспоненте) стремиться к новому установившемуся значению. Выходной сигнал всегда запаздывает по отношению к входному (Примеры апериодического звена: цепи LR и LC, термопары, термостаты, магнитные усилители).

Колебательное звено – звено, у которого при ступенчатом (скачкообразном) изменении входной величины, выходная величина стремиться к новому установившемуся значению, совершая при этом затухающие и незатухающие колебания (Примеры: контур RLC, масса, подвешенная на пружине, маятник, поплавковый уровнемер).

У каждого динамического звена может быть только одна входная и одна выходная величина. Причем выходная величина не должна оказывать на это звено обратного влияния, т.е. при соединении звеньев любое воздействие распространяется только от входа к выходу. Это свойство динамических звеньев называется свойством однонаправленности.

Кроме того, подключение каждого последующего звена не должно влиять на процессы, происходящие в предыдущем звене. Это свойство динамического звена называется независимостью звеньев.

Любое динамическое звено математически может быть изображено следующим образом:

Х_вх (x) Х_вых (y)

Рисунок 15.1. Математическое изображение динамического звена

где W(p) – передаточная функция – отношение изменения во времени сигнала на выходе звена Х_вых(t) к изменению сигнала на входе того же звена Х_вх(t) при нулевом начальном условии.

Для суммирующих элементов используют специальное обозначение – круг, разбитый на сектора. Если сектор залит чёрным цветом, поступающий в него сигнал вычитается, а не складывается с другими. Разветвление сигнала обозначается точкой, как и в радиотехнике.

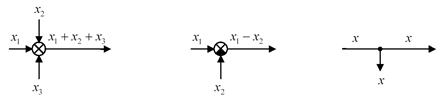
Рисунок 15.2.Геометрическое изображение суммирующего элемента

Математически звенья описываются линейными дифференциальными уравнениями первого или второго порядка:

(15.1)

(15.2)

где d – дифференциал;

Для удобства расчетов введем оператор дифференцирования (D) или

Тогда передаточная функция звена будет иметь вид:

(15.3)

Это выражение и вписывается в прямоугольник для каждого конкретного звена.

Например, если звено описывается дифференциальным уравнением

T(dXвых/dt) +Xвых = K Xвх, (15.4)

а оператор p = d/dt, то в операторной форме это уравнение будет иметь вид:

(Tp + 1) Xвых(p) = KXвх (p); (15.5)

Передаточная функция такого звена будет иметь вид:

W(p) = (Tp + 1) / K. (15.6)