Основные формы, области применения и основные расчёты

К пространственным деревянным конструкциям или, как их часто принято называть, к покрытиям-оболочкам относят покрытия с изогнутой поверхностью, в которых все составляющие элементы работают совместно как единое целое. Оболочки благодаря такой поверхности менее материалоёмки, чем плоские конструкции и являются совмещённым видом покрытия, т.к. способны выполнять одновременно несущую и ограждающую функции. Они могут иметь многообразные формы различного функционального назначения.

К основным конструктивным типам пространственных деревянных конструкций относятся:

1)распорные своды при прямоугольном плане и опирании на

продольные стены;

2)складки и своды оболочки, опёртые в основном только на поперечные торцевые стены, а также оболочки двоякой положительной или отрицательной кривизны;

3)купола, опёртые по контуру круглого или многоугольного здания.

Указанные типы деревянных конструкций могут быть выполнены в виде:

· тонкостенных оболочек;

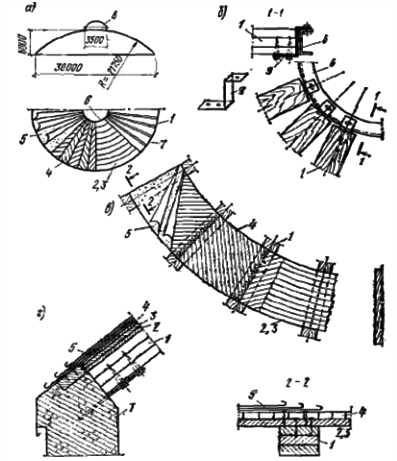
Рисунок 12.1 – Тонкостенный купол-оболочка:

а – поперечный разрез и план; б – примыкание к верхнему опорному кольцу; в – детали покрытия; г – примыкание к нижнему опорному кольцу; 1 – дощатые ребра; 2 – нижний слой кольцевого настила; 3 – верхний слой кольцевого настила; 4 – косой настил; 5 – кровля; 6 – верхнее опорное кольцо; 7 – нижнее железобетонное опорное кольцо; 8 – фонарь;

9 – металлическая деталь крепления ребер

· ребристых складок и оболочек, в которых для увеличения жёсткости тонкостенные элементы усилены рёбрами

Рисунок 12.2 – Клеефанерный свод из криволинейных ребристых панелей

· сетчатых систем.

Рисунок 12.3 – Кружально-сетчатый свод

Применение перечисленных пространственных деревянных конструкций целесообразно в следующих случаях:

· когда необходимо использовать внутренний габарит при малой строительной высоте конструкций (область применения сводов-оболочек и куполов);

· если в продольных стенах необходимы большие проёмы для ворот (например, в ангарах) и опирание должно осуществляться на торцевые стены (это область применения сводов-оболочек и складок);

· в покрытиях над круглыми, овальными, квадратными и многоугольными в плане помещениями (область применения куполов).

Пространственные деревянные конструкции используются для покрытий различных промышленных, общественных и сельскохозяйственных зданий: спортивных залов, зерноскладов, выставочных павильонов, театральных и концертных залов, крытых рынков и т.п.

Наша страна обладает приоритетом в области пространственных деревянных конструкций, у нас разработаны многие их современные виды.

Длительная эксплуатация пространственных конструкций как у нас в стране, так и за рубежом свидетельствует об их надёжности и долговечности. Построенные в нашей стране свыше трех десятков лет назад деревянные своды и купола продолжают эксплуатироваться и находятся в хорошем состоянии. За рубежом пространственные деревянные конструкции всё шире применяют для перекрытия уникальных по размерам пролётов.

Рассмотрим основные типы пространственных деревянных конструкций, придерживаясь их классификации.

Распорные своды

Оболочки в виде сводов имеют цилиндрическую форму поверхности и опираются по сторонам, параллельным образующим. Существует два основных вида распорных сводов:

· тонкостенный клеефанерный свод стрельчатого или кругового очертания с затяжкой или с передачей распора непосредственно опорам

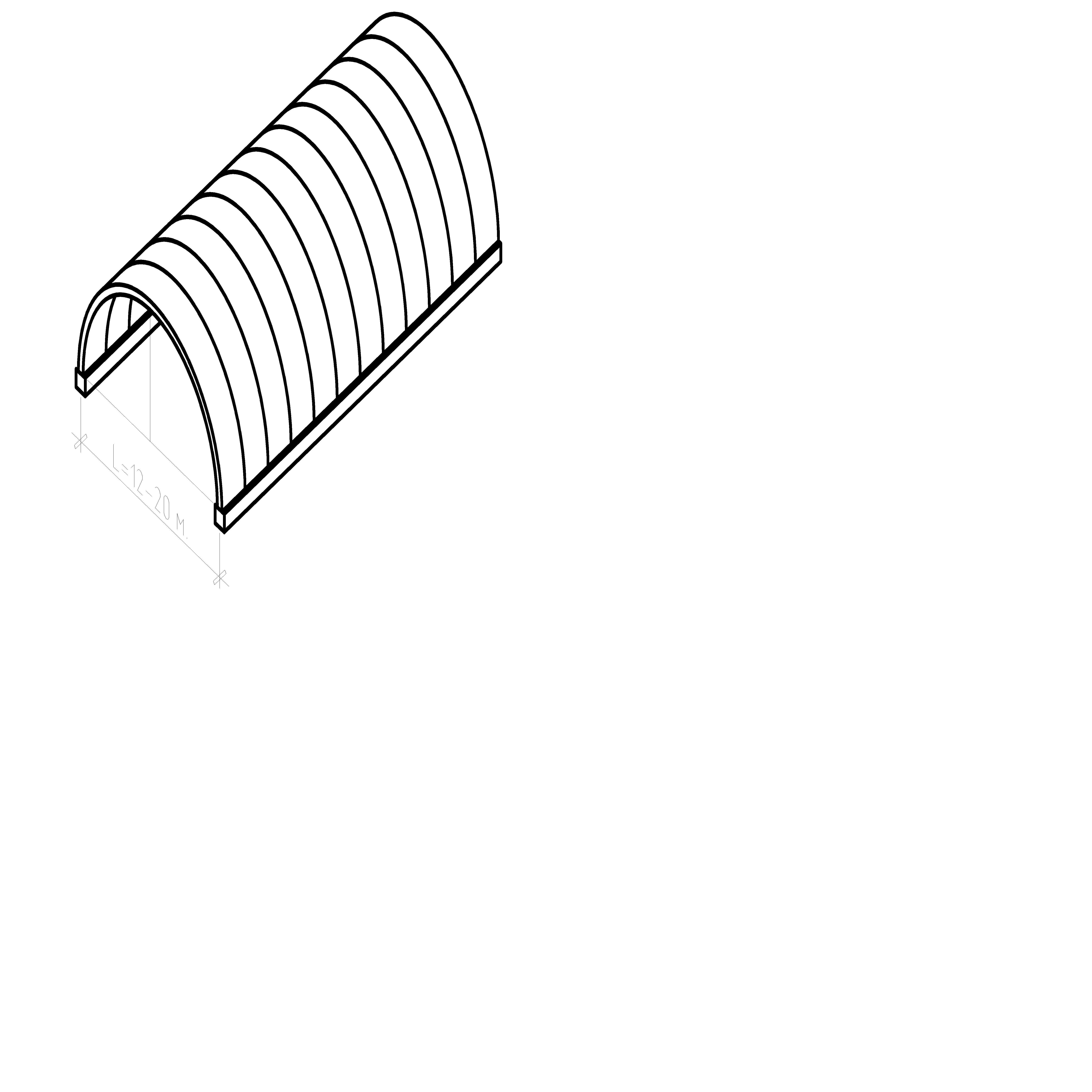
Рисунок 12.4 – Тонкостенный клеефанерный свод кругового очертания с затяжкой сборной конструкции

· кружально-сетчатый свод кругового или стрельчатого очертания с затяжкой или с передачей распора на стены

Рисунок 12.5 – Кружально-сетчатый свод кругового очертания с передачей распора на стены

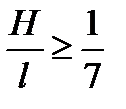– для сводов круговых;

– для стрельчатых сводов.

Кружально-сетчатые своды являются наиболее распространёнными пространственными конструкциями. Состоят они из косяков (цельных или клеефанерных). Пролёт сводов из цельных косяков l=12-20 м, из клеефанерных l=20-100 м.

Основные узлы сетки образуются из трёх косяков, один из которых является сквозным и проходит через узел не прерываясь, а два других набегающих косяка примыкают к сквозному.

В зависимости от конструкции косяков и их соединения между собой различают:

· безметальные кружально-сетчатые своды системы архитектора С.И.Песельника;

· кружально-сетчатые своды с узлами на болтах системы Цолльбау;

· своды из составных клеефанерных косяков.

Своды системы Песельника изготовляются из косяков цельного сечения, имеющих на концах шипы, а посередине сквозное гнездо.

В каждом узле сетки сопрягаются три косяка, из которых два набегающих входят с двух сторон своими шипами в гнездо сквозного косяка. Верхняя кромка косяка может быть криволинейной, либо с одним или двумя переломами, шаг сетки свода с = 0,8–1,5 м, тогда длина косяков оказывается порядка 2 м.

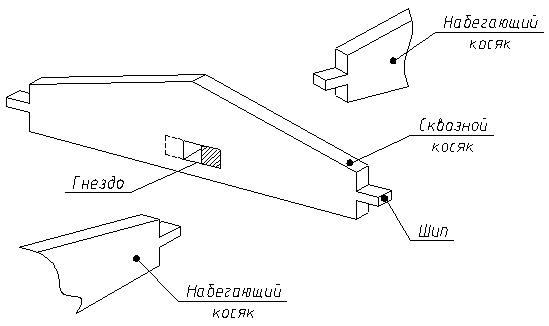
Рисунок 12.6 – Косяки безметального свода с узлами на шипах

В безметальном кружально-сетчатом своде применяется сетка как прямоугольная, так и косоугольная с углом φ = 45°.

Узловое соединение может быть нецентрированное, когда оси набегающих косяков не совпадают и центрированное, когда оси совпадают. В последнем случае шип имеет клиновидную форму.

а)

б)

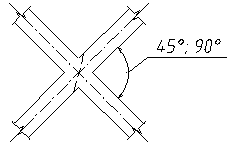
Рисунок 12.7 – Узлы безметального свода с узлами на шипах:

а – нецентрированный; б – центрированный

Кружально-сетчатые своды с узлами на болтах (системы Цолльбау) имеют косяки с круглыми отверстиями на концах (под болты) и овальными отверстиями посередине косяка.

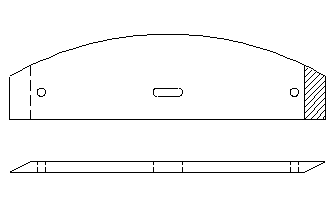
Рисунок 12.8 – Косяк свода с узлами на болтах

В узлах соединения косяков набегающие косяки путём натяжения болта плотно прижимаются к косяку.

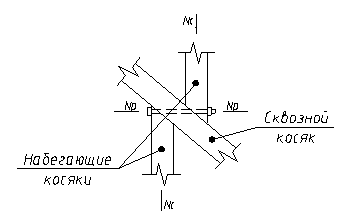
Рисунок 12.9 – Основной (средний) узел свода системы Цолльбау

Своды из клеефанерных косяков могут выполняться в безметальном и метальном вариантах. В первом случае косяки соединяются в узлах на врубках подобно тому, как это делается в сводах Песельника. Косяки имеют коробчатую форму сечения.

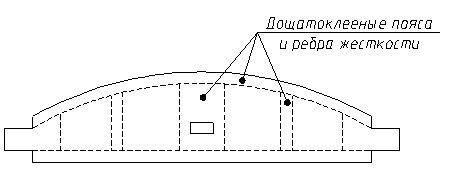
Рисунок 12.10 – Клеефанерный косяк безметалльного свода

Конструкция и расчёт составных косяков аналогичны конструкции и расчёту клеефанерных балок.

Все ранее рассмотренные соединения косяков сетки кружально-сетчатых сводов являются шарнирными. Изгибающий момент в узлах сеток воспринимается только сквозными косяками.

В метальном варианте свода из клеефанерных косяков устраивают бесшарнирное соединение косяков, когда изгибающий момент в узле воспринимается не только сквозным, но и набегающими косяками.

Это достигается путём соединения набегающих косяков по верхним и нижним граням с помощью вклеенных металлических стержней.

Расчёт сетчатого свода. При расчете выделяют расчётную полосу свода, соответствующую шагу решётки. Затем определяют продольные силы N_a и изгибающие моменты M_a, как в арке постоянной жёсткости с соответствующей схемой опирания.

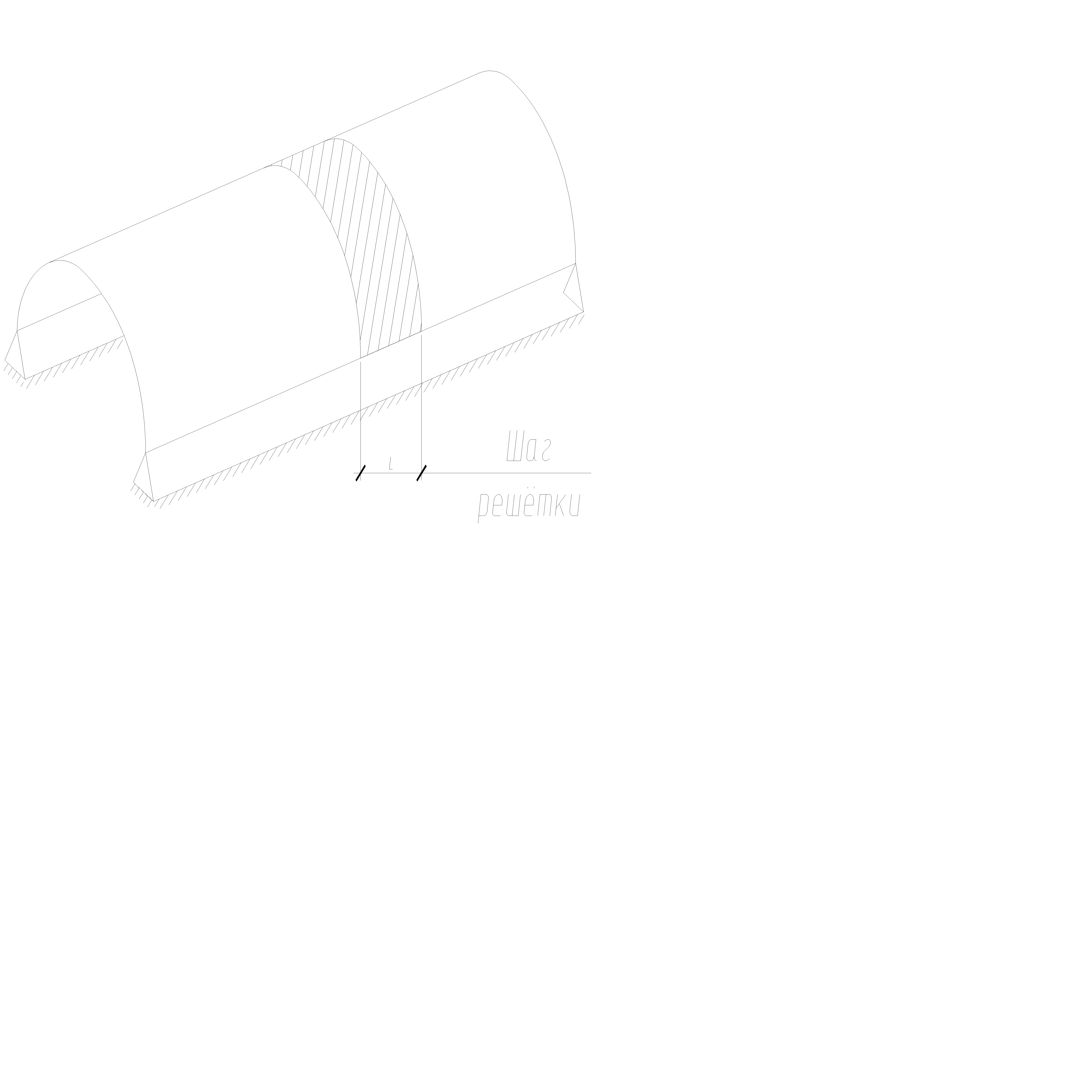
Рисунок 12.11 – Выделение из свода расчетной полосы

Если угол между образующей свода и сквозным косяком – α, то изгибающий момент, воспринимаемый косяком при шарнирном соединении косяков, когда момент воспринимается только одним сквозным косяком, будет

,

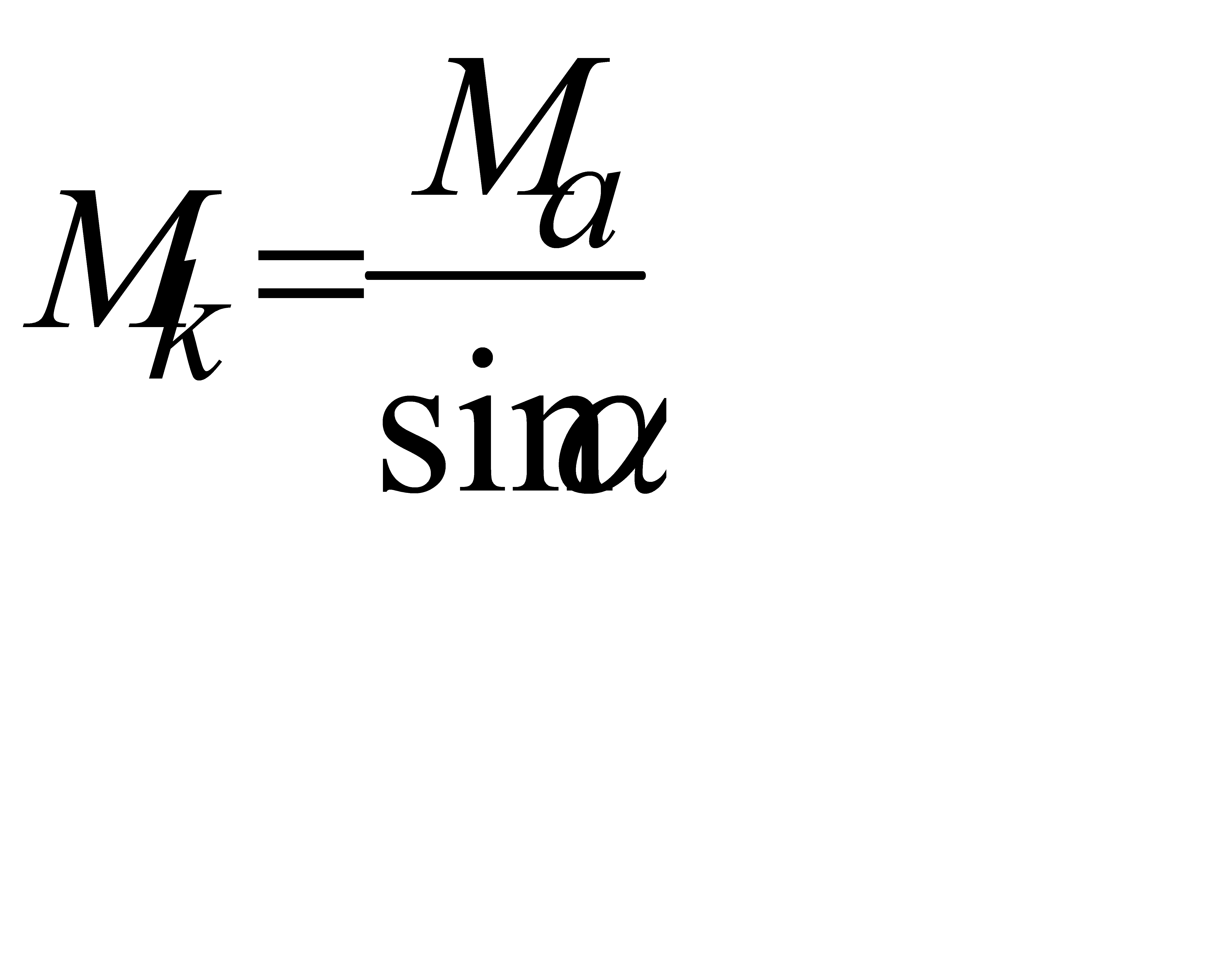а для косяков сводов с бесшарнирными узлами, когда набегающий косяк тоже воспринимает изгибающий момент

.

Сжимающее усилие, приходящееся на один косяк, определяется аналогично

.

Проверку прочности косяка производят как сжато-изгибаемого элемента по формуле

,

где К_ф – коэффициент фронтонов, увеличивающий жёсткость покрытия, берётся по таблице IX.1 [1].

Своды-оболочки и складки. Традиционный свод-оболочка представляет собой покрытие цилиндрической формы, опёртое на торцевые стены.

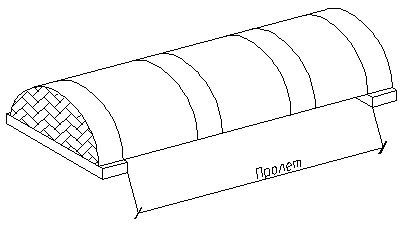
Рисунок 12.12 – Свод-оболочка с опиранием на торцовые стены

В сводах-оболочках отсутствует распор, свойственный сводам, опёртым по продольным сторонам, поэтому нет необходимости устраивать в них затяжки или контрфорсы.

По статической схеме и характеру работы к сводам-оболочкам близки призматические складки, поверхность которых образована наклонными плоскими гранями.

Своды-оболочки и складки выполняют в однорядном и многорядном вариантах.

Рисунок 12.13 – Призматическая однорядная складка треугольного очертания

Многорядные складки и оболочки. Могут быть трех видов: тонкостенные, ребристые и трехслойные. В первом случае сечение покрытия может быть сплошным (склеенные между собой дощатые настилы) или каркасным (к каркасу из брусьев высотой до 15 см на гвоздях и клею с одной стороны или двух сторон крепятся обшивки из фанеры, древесностружечных плит или досок).

Рисунок 12.14 – Многорядные: призматическая складка треугольного очертания и свод-оболочка

Во втором варианте, в настоящее время устаревшем, жёсткие рёбра располагают в поперечном направлении с шагом 2-6 м, а по ним укладывают продольный настил (для восприятия продольных усилий) и два косых настила под углом друг к другу (для восприятия сдвигающих усилий), иногда по рёбрам вместо настилов укладывают листы фанеры, обеспечивающие восприятие продольных и сдвигающих усилий.

Трехслойные элементы изготавливают чаще всего из пластмасс – с обшивками из стеклопластика или жесткого пливинилхлорида со средним слоем из пенопласта. Вместо стеклопластика могут быть применены обшивки из фанеры.

Расчёт свода оболочки или призматической складки при соотношении пролёта l₁ к длине волны l₂ 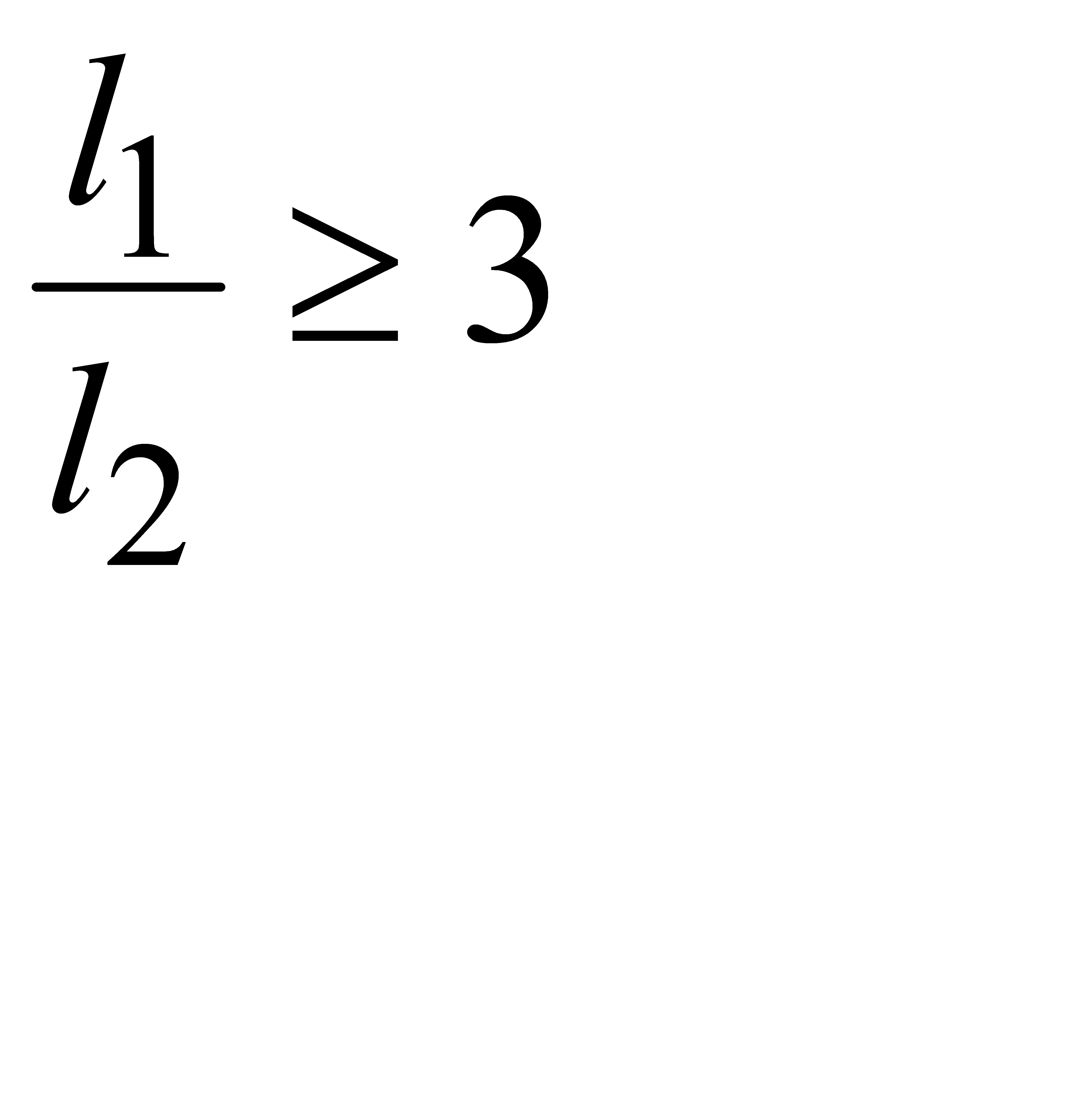(длинная оболочка) в продольном направлении на симметричную нагрузку можно выполнять как для балки корытообразного сечения.

В такой балке для вычисления напряжения можно использовать формулы сопротивления материалов. При расчёте вычисляют нормальные продольные и сдвигающие усилия, а также изгибающие моменты от собственного веса, снега и ветра. Далее проверяют прочность и устойчивость по элементам.

Принимается следующее распределение внутренних усилий между элементами оболочки: нормальные продольные усилия N₁ воспринимаются продольным настилом и усиленными (в поясах ) частями его, сдвигающие усилия Т₁ воспринимаются двойным косым настилом, изгибающие моменты М₁ и М₂ воспринимаются рёбрами жёсткости и поперечным настилом.

Такой расчёт является приближённым, точный расчёт оболочек выполняют по теории оболочек Власова.

В зарубежной практике нашли применение деревянные тонкостенные своды-оболочки: двоякой положительной и отрицательной кривизны, воронкообразные, бочарные оболочки и оболочки в виде гиперболических параболоидов (покрытия типа гипар).

Рисунок 12.15 – Воронкообразное покрытие-оболочка

Покрытие типа гипар. Гипар – это покрытие, состоящее из пролетного строения и бортовых элементов (рисунок 12.16). Оболочка выполняется в зависимости от величины пролета из двух-четырех рядов шпунтованных досок или брусков, склеенных между собой или соединённых гвоздями. Слои располагаются под углом 45⁰ относительно один другого.

Оболочки могут выполняться из фанерных полос, укладываемых в два или три слоя.

Оболочки двоякой кривизны являются оболочками построечного изготовления. Возводят их с помощью сплошных лесов или подмостей, по которым укладывают кружала и с которых ведут сборку отдельных слоёв оболочки. Покрытие типа гипар может выполняться и в сборном варианте из прямоугольных панелей, склеенных из трёх слоёв досок.

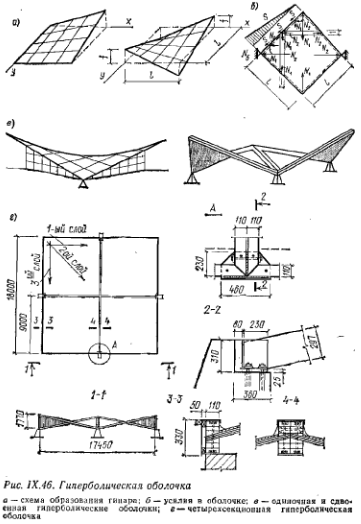
Рисунок 12.16 – Гиперболическая оболочка:

а – схема образования гипара; б – усилия в оболочке; в – однорядная и сдвоенная гиперболические оболочки

Купола. В зависимости от конструктивного решения купола могут быть тонкостенными, ребристыми и сетчатыми. Для пролётов от 12 до 35 м применяют тонкостенные сетчатые купола. При пролётах от 35 до 120 м и более в целях увеличения жёсткости применяют рёбристые купола-оболочки.

Ребристые купола могут быть сферическими, многогранными или складчатыми.

Рисунок 12.17 – Сферический купол

Рисунок 12.18 – Многогранный купол

Рисунок 12.19 – Складчатый купол

Состоят ребристые купола из радиально расположенных рёбер, опирающихся на нижние и верхние опорные кольца.

Шаг рёбер от 3 до 6 м по нижнему поясу. В ребристых куполах по аркам идут прогоны, по прогонам укладывается в два слоя настил из досок – продольный и косой под углом 45° к прогонам.

Нижнее опорное кольцо работает на растяжение и выполняется железобетонным. Верхнее кольцо работает на сжатие и может быть деревянным. Соединения полуарок с кольцами рекомендуется выполнять шарнирными. В расчёте арок жёсткость прогонов и настила не учитывается.

Расчёт ребристого купола ведётся путём расчленения на арки с соответствующей грузовой площадью. В остальном порядок расчёта полностью совпадает с расчётом дощатоклееных трёхшарнирных арок.

Пространственная неизменяемость и устойчивость плоской формы изгиба рёбер обеспечивается установкой связей (горизонтальных и вертикальных).

Кружально-сетчатые купола могут быть сферическими или из сомкнутых сводов

Рисунок 12.20 – Сетчатый купол и кружально-сетчатый купол из сомкнутых сводов

Сетка может быть ромбической и прямоугольной, узлы решены на врубках или болтах. При числе граней шесть и менее сектор купола рассчитывается по аналогии с сетчатым сводом, а при числе граней более шести – по приближённой безмоментной теории расчета сферических куполов-оболочек.

Представляет интерес конструкция сомкнутого свода, разработанная в США для пролёта 257 м (самый крупный в мире из перекрываемых пролётов). Проект этого свода предусматривает использование его для покрытия стадионов в четырёх городах США.

Гурты (рёбра на стыках граней свода) клееные переменного коробчатого сечения. Максимальная высота сечения 334 см.

Рисунок 12.21 – Сомкнутый сетчатый свод пролетом 257 м (проект):

а – схема купола; б – сечение гурта

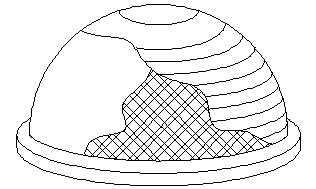
Тонкостенные купола-оболочки. Деревянные тонкостенные купола-оболочки состоят из меридианных ребер (арочек), кольцевого и косого настилов, верхнего кружального и нижнего опорного кольца.

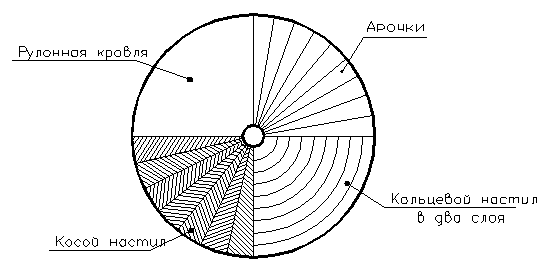
Рисунок 12.22 – План тонкостенного купола-оболочки

Расстояние между осями арочек по опорному кольцу назначается от 0,8 до 1,5 м. Высота арочек h для придания куполу достаточной жёсткости должна составлять не менее 1/250 его пролёта. На арочки гвоздями прибивают оба слоя кольцевого настила, а затем косой настил в «ёлочку» под углом ~ 45°.

Расчёт куполов-оболочек с достаточной точностью ведётся по безмоментной теории оболочек

Рисунок 12.23 – Геометрическая и расчетная схемы купола-оболочки

При расчёте принимается, что меридианные элементы и рёбра куполов воспринимают меридиональные усилия Т₁, кольцевые настилы – кольцевые усилия Т₂, а косые настилы – сдвигающие усилия S.

Усилия Т₁, Т₂ и S находят при трёх схемах загружения:

· 1 схема – собственный вес купола (рисунок 12.23). Усилия в рёбрах Т₁ в точке А определится по формуле

,

где: Q_φ – вес всей вышележащей части купола;

m – число рёбер.

Усилия Т₂ в кольцевом настиле на единицу ширины определится по формуле:

,

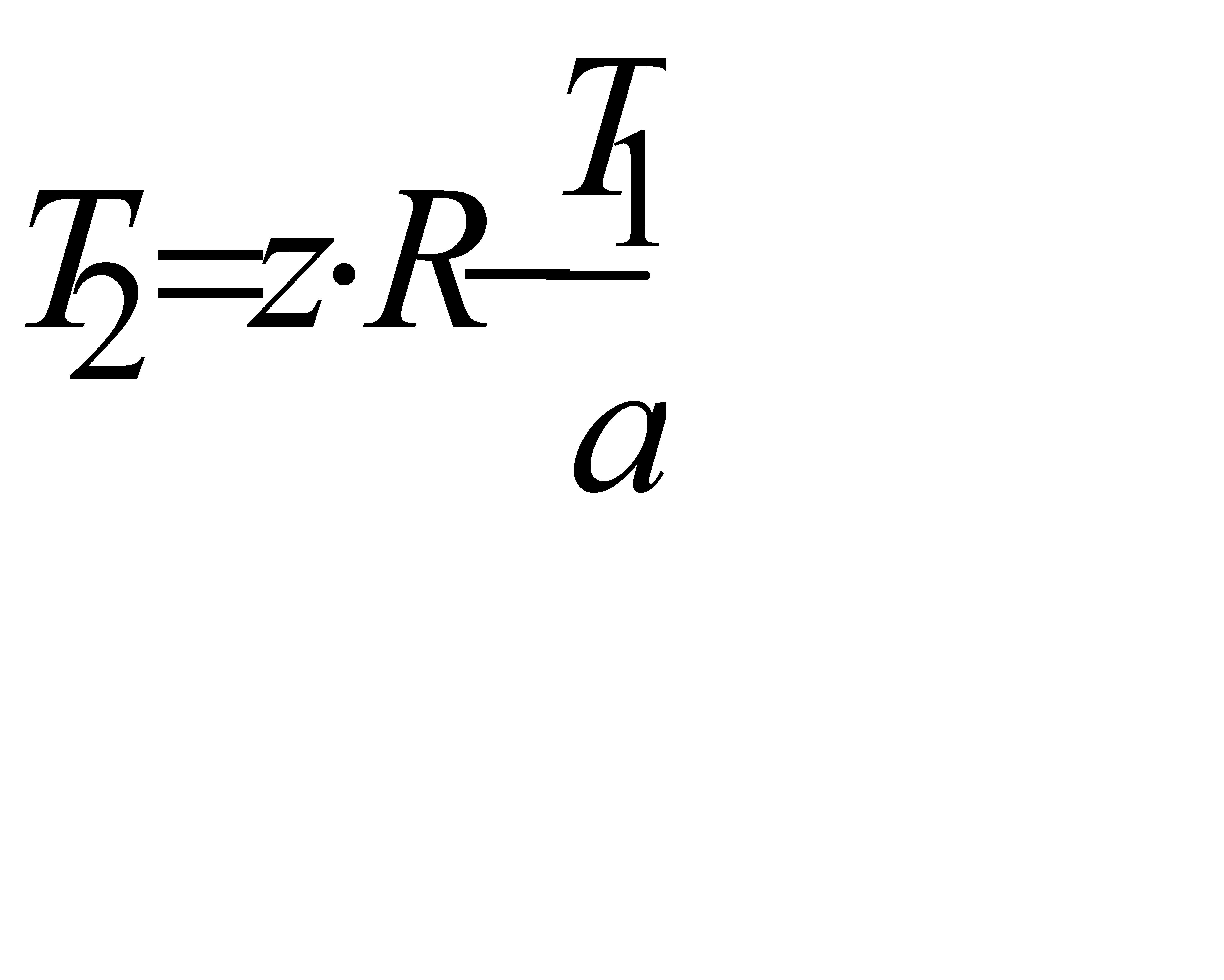где z – проекция на нормаль равномерно распределённой нагрузки (кровля, косой и кольцевой настилы) и веса рёбер;

R – радиус сферы купола;

Т₁ – меридиональное усилие в рассматриваемой точке А;

а – расстояние между рёбрами.

Сдвигающее усилие S при симметричной нагрузке равно нулю (S=0).

· 2 схема – снеговая нагрузка на всём пролёте (рисунок 12.23). Она принимается с учётом изменения интенсивности по поверхности купола по закону косинуса, что даёт равномерную нагрузку по плану интенсивностью р₀. Меридианные усилия:

,

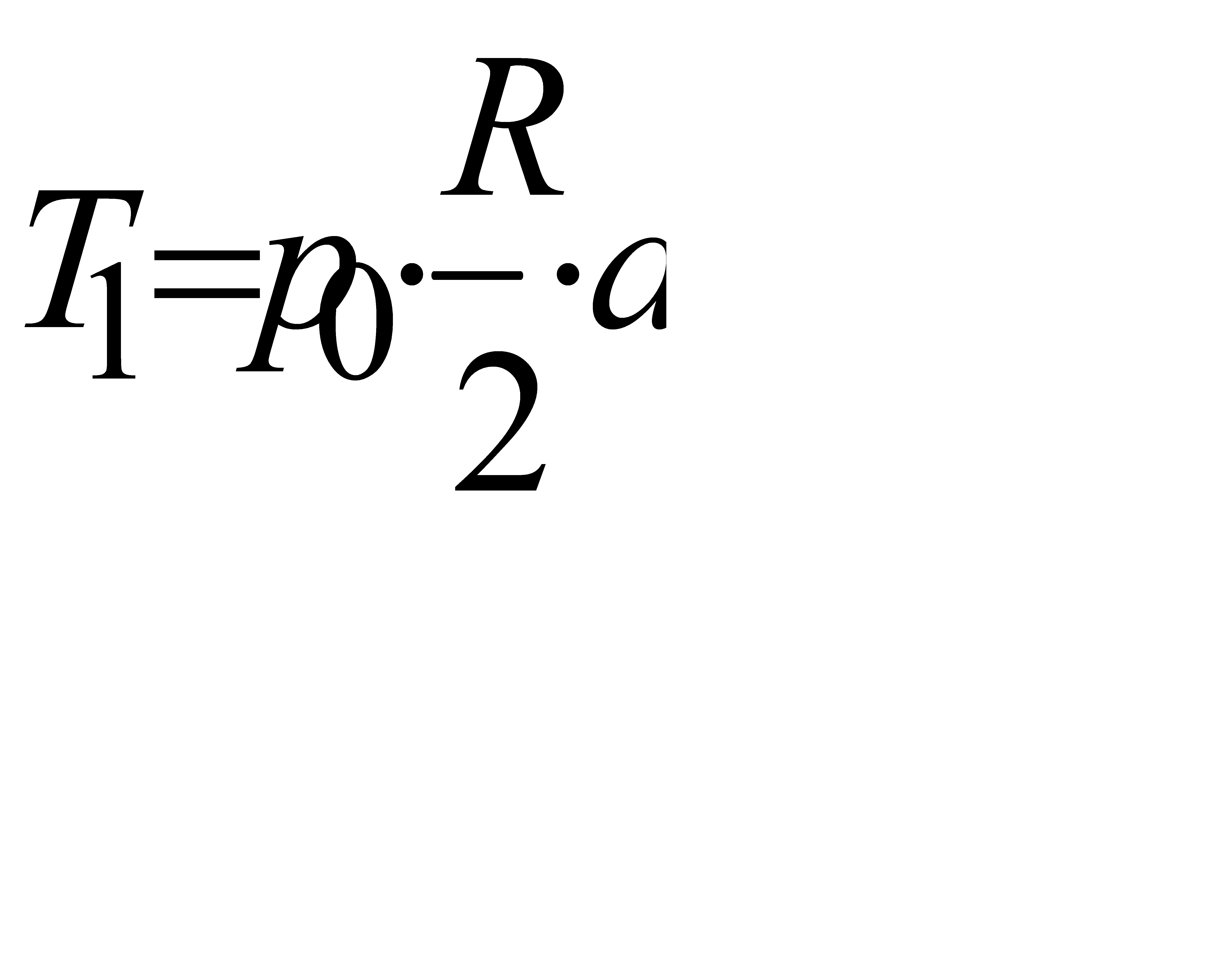Кольцевые усилия:

,

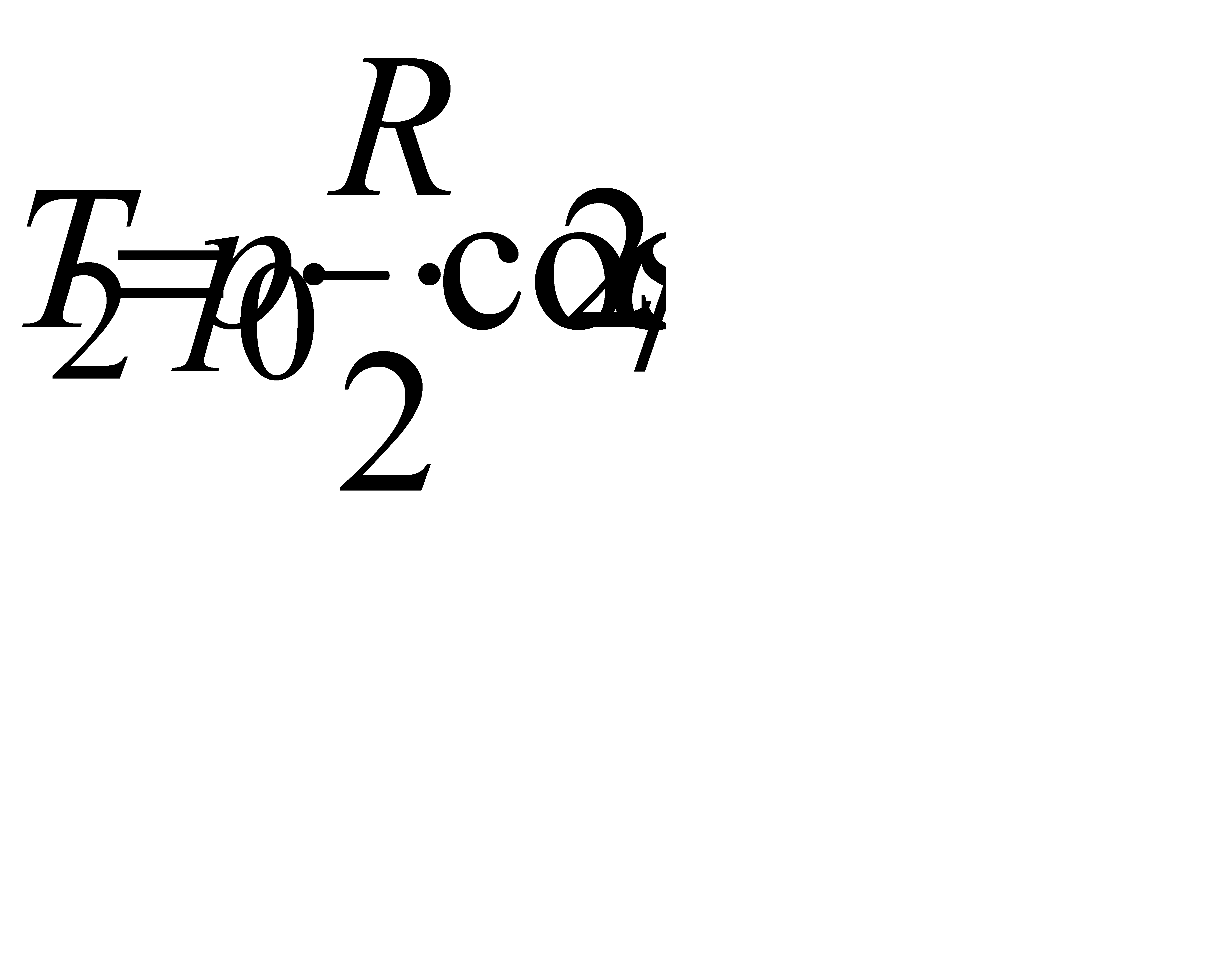Сдвигающие усилия:

.

· 3 схема – ветровая нагрузка (рисунок 12.24). Действительная эпюра давления ветра заменяется более простыми эпюрами: симметричной и кососимметричной.

Рисунок 12.24 – Эпюра ветрового давления на купол в поперечном сечении

Усилия от симметричной эпюры определяются по следующим формулам:

меридиональные усилия:

,

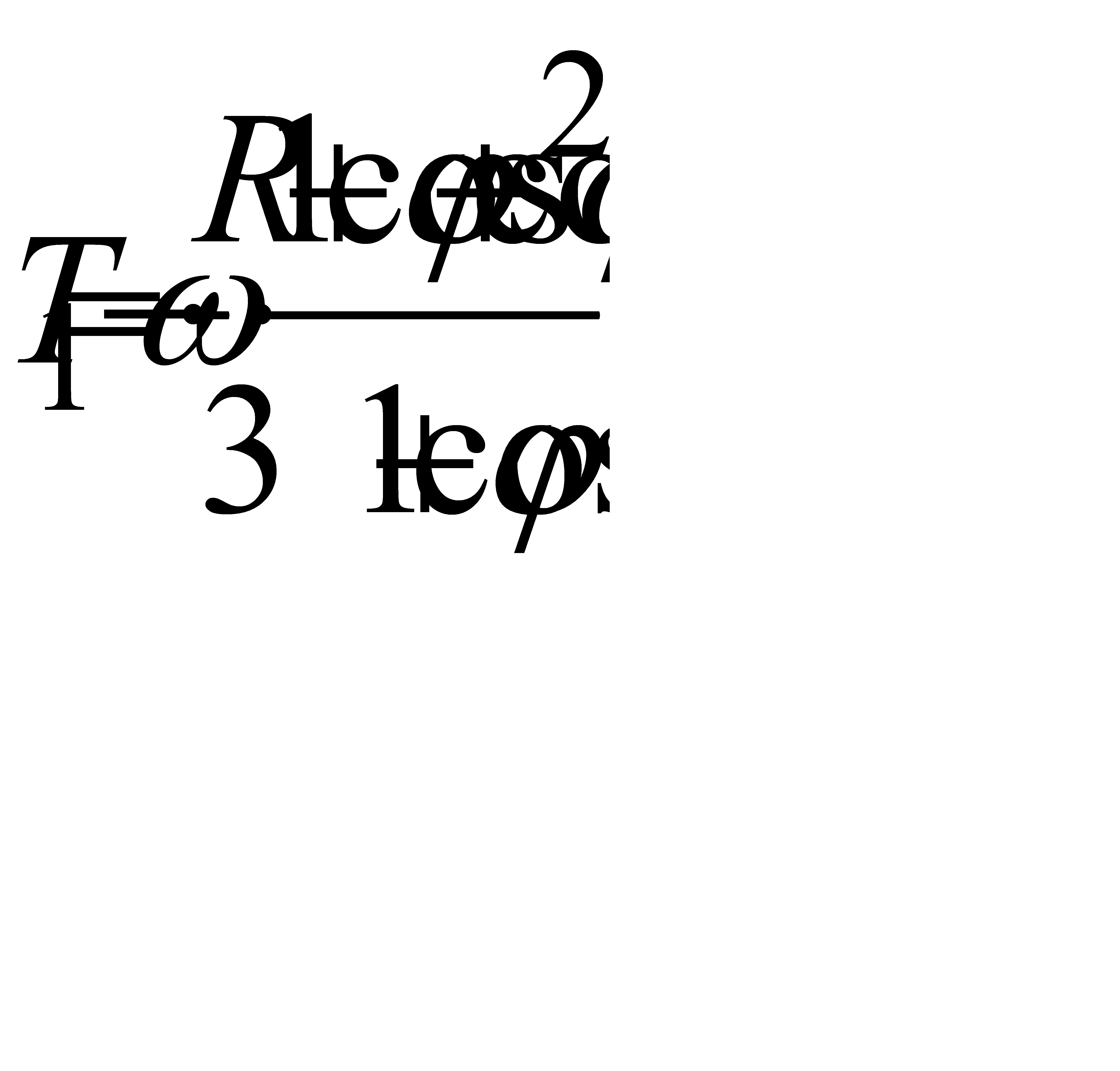кольцевые усилия:

,

сдвигающие усилия:

Усилия от кососимметричной эпюры можно определить по таблицам книги Дишингера «Оболочки, тонкостенные железобетонные купола и своды», М. 1971 г.

Кососимметрическая нагрузка даёт сдвигающие усилия, на который рассчитывается косой настил.

Проверка сечений элементов

· Определив расчётное значение Т₁ на одно ребро (как максимальное при различных сочетаниях усилий при трёх перечисленных схемах загружения), ребро проверяют на сжатие и смятие торцов в опорных кольцах.

· Кольцевой настил проверяют на смятие (в сжатой зоне) по полной площади. В растянутой зоне проверка на растяжение ведётся по площади

F_нт= 0,5∙F_бр.

· Сдвигающие усилия S вызывают в косом настиле сжатие или растяжение. По этим усилиям подбирают сечение досок и связи (гвозди, шурупы, клей).

· Верхнее кружальное кольцо проверяют на сжатие и смятие в стыке

N₁= T₁∙r₁,

где: Т₁ – сжимающее усилие в ребре;

r₁ – радиус кольца.

· Нижнее опорное кольцо проверяют на растяжение на усилие

N_р= H₁∙r₂,

где: Н₁ – распор купола на единицу длины опорного кольца;

r₂ – радиус опорного кольца.