Растянутые элементы

На растяжение работают нижние пояса и отдельные раскосы ферм, затяжки арок и других сквозных конструкций. Растягивающее усилие N действует вдоль оси элемента и во всех точках его поперечного сечения возникают растягивающие напряжения σ, которые с достаточной точностью считаются одинаковыми по величине.

Древесина на растяжение работает почти упруго и показывает высокую прочность. Разрушение происходит хрупко в виде почти мгновенного разрыва. Стандартные образцы при испытаниях на растяжение имеют вид «восьмерки».

Как видно из диаграммы растяжения древесины без пороков, зависимость деформаций от напряжений близка к линейной, а прочность достигает

100 МПа.

Однако прочность реальной древесины при растяжении, учитывая ее значительные колебания, большое влияние пороков и длительности нагружения значительно ниже: так для неклееной древесины 1 сорта R_р=10 МПа, для клееной древесины влияние пороков уменьшается, поэтому R_р=12 МПа. Проверочный расчет растянутых элементов производится по формуле:

σ ,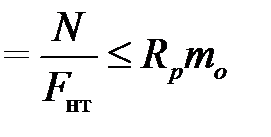

где

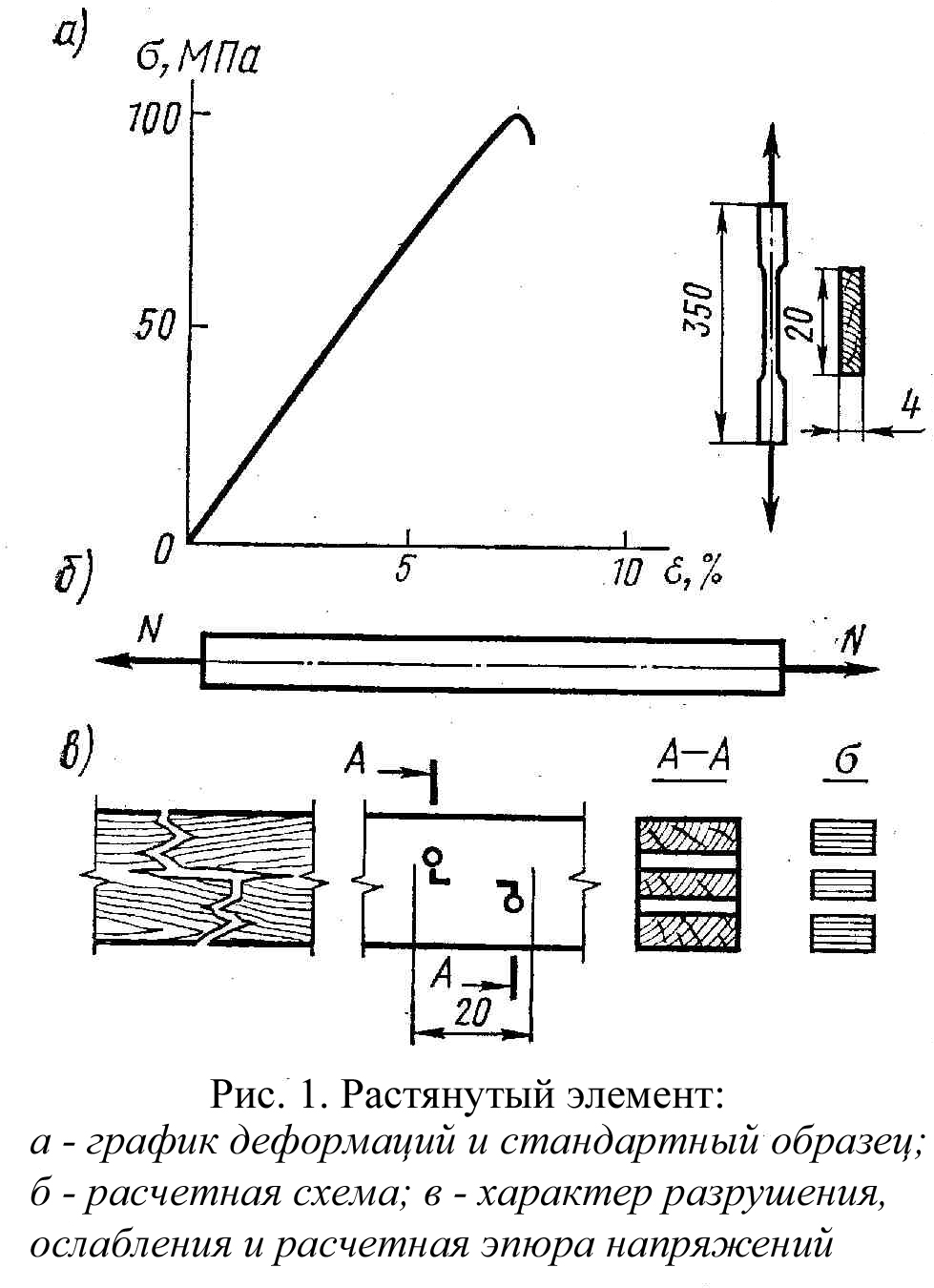Рисунок 2.1 – Растянутый элемент: а – график деформаций и стандартный образец; б – расчетная схема; в – характер разрушения, ослабления и расчетная эпюра напряжений

F_нт.– площадь рассматриваемого поперечного сечения, причем ослабления, расположенные на участке длиной

20 см считаются совмещенными в одном сечении. Для подбора сечений пользуются этой же формулой, но относительно искомой (требуемой) площади F_тр. Прочность растянутых элементов в тех местах, где есть ослабления, снижается в результате концентрации напряжений у их краев. Это учитывается коэффициентом условия работы m₀=0,8.

Сжатые элементы

На сжатие работают стойки, подкосы, верхние пояса и отдельные стержни ферм. В сечениях элемента от сжимающего усилия N, действующего вдоль его оси, возникают почти одинаковые по величине сжимающие напряжения σ (эпюра прямоугольная).

Стандартные образцы при испытании на сжатие имеют вид прямоугольной призмы с размерами, указанными на рисунке 2.2.

Древесина работает на сжатие надежно, но не вполне упруго. Примерно до половины предела прочности рост деформаций происходит по закону близкому к линейному, и древесина работает почти упруго. При росте нагрузки увеличение деформаций все более опережает рост напряжений, указывая на упруго-пластический характер работы древесины.

Разрушение образцов без пороков происходит при напряжениях, достигающих 44 МПа, пластично, в результате потери устойчивости ряда волокон, о чем свидетельствует характерная складка. Пороки меньше снижают прочность древесины, чем при растяжении, поэтому расчетное сопротивление реальной древесины при сжатии выше и составляет для древесины 1 сорта

R_с=14÷16 МПа, а для 2 и 3 сортов эти величины немного ниже.

Расчет на прочность сжатых элементов производится по формуле

,

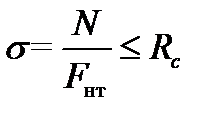где

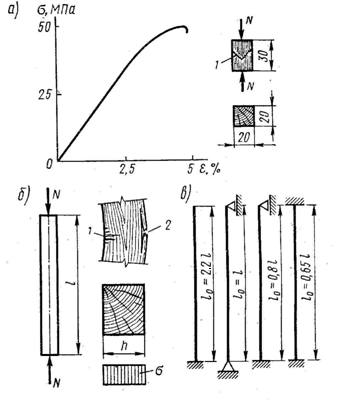Рисунок 2.2 – Сжатый элемент: а – график деформаций и стандартный образец; б – расчетная схема, характер разрушения и эпюра напряжений; в – типы закреплений концов и расчетные длины

R_с – расчетное сопротивление сжатию.

Аналогичным образом рассчитываются и сминаемые по всей поверхности элементы. Сжатые стержни, имеющие большую длину и незакрепленные в поперечном направлении должны быть, помимо расчета на прочность, рассчитаны на продольный изгиб. Явление продольного изгиба заключается в том, что гибкий центрально-сжатый прямой стержень теряет свою прямолинейную форму (теряет устойчивость) и начинает выпучиваться при напряжениях, значительно меньших предела прочности. Проверку сжатого элемента с учетом его устойчивости производят по формуле

σ ,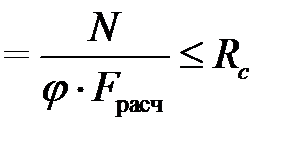

где

F_расч – расчетная площадь поперечного сечения,

φ – коэффициент продольного изгиба.

F_расч принимается равной:

1. При отсутствии ослаблений F_расч = F_бр,

2. При ослаблениях, не выходящих на кромки, если площадь ослаблений не превышает 25% F_бр, F_расч = F_бр,

3. То же, если площадь ослаблений превышает 25% F_бр, F_расч = 4/3F_нт,

4. При симметричных ослаблениях, выходящих на кромки F_расч = F_нт.

При несимметричных ослаблениях, выходящих на кромку, элементы рассчитывают как внецентренно-сжатые.

Коэффициент продольного изгиба φ всегда меньше 1 и определяется в зависимости от расчетной длины элемента l₀, ирадиуса инерции сечения r и его гибкости λ. Гибкость элемента λ равна отношению расчетной длины l₀ к радиусу инерции сечения элемента

; .

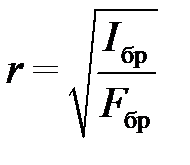Расчетную длину элемента l₀ следует определять умножением его свободной длины l на коэффициент μ₀

l₀=l μ₀, где

коэффициент μ₀ принимается в зависимости от типа закрепления концов элемента:

- при шарнирно закрепленных концах μ₀=1;

- при одном шарнирно закрепленном, а другом защемленном μ₀=0,8;

- при одном защемленном, а другом свободном нагруженном конце μ₀=2,2;

- при обоих защемленных концах μ₀=0,65.

Гибкость сжатых элементов ограничивается с тем, чтобы они не получились недопустимо гибкими и недостаточно надежными. Отдельные элементы конструкций (колонны, сжатые пояса, опорные раскосы и опорные стойки ферм) должны иметь гибкость не более 120. Прочие сжатые элементы основных сквозных конструкций – не более 150, сжатые элементы связей – 200.

При гибкости более 70 (λ>70) сжатый элемент теряет устойчивость, когда напряжения сжатия в древесине еще невелики, и она работает упруго.

Коэффициент продольного изгиба (или коэффициент устойчивости), равный отношению напряжения в момент потери устойчивости σ_кр к пределу прочности при сжатии R_пр, определяют по формуле Эйлера с учетом постоянного отношения модуля упругости древесины к пределу прочности:

,

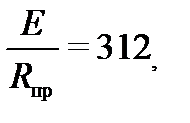
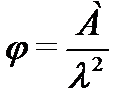где А=3000 – для древесины,

А=2500 – для фанеры.

При гибкостях, равных и меньших 70 (λ≤70) элемент теряет устойчивость, когда напряжения сжатия достигают упругопластической стадии и модуль упругости древесины понижается. Коэффициент продольного изгиба при этом определяют с учетом переменного модуля упругости по упрощенной теоретической формуле

,

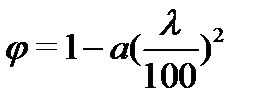где a=0,8 – коэффициент для древесины;

a=1 – коэффициент для фанеры.

При подборе сечения используют формулу расчета на устойчивость, предварительно задаваясь величиной λ и φ.