Решение. Рассмотрим равновесие балки АВ, к которой приложены как заданные, так и искомые силы
Рассмотрим равновесие балки АВ, к которой приложены как заданные, так и искомые силы. Освобождаем балку от связей и заменяем их действие реакциями (рис. 1.14,6). Получили плоскую систему сил.
Выбираем систему координат (см. рис. 1.14,6).
Составляем три уравненияравновесия:
 |
Решая второе и третье уравнения, получаем:
 |
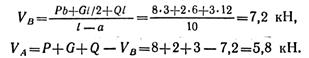
Составим проверочное уравнение
следовательно, опорные реакции определены верно.
Пример 7. Для заданной балки (рис. 1.15, а) определить опорные реакции.
Решение
Рассмотрим равновесие балки АВ, к которой приложены все заданные и искомые силы. Освободим балку от связей и заменим их действие реакциями (рис. 1.15, б). Получили плоскую систему произвольно расположенных сил.
Выбираем систему координат (см. рис. 1.15, 6). Для полученной системы сил в рассматриваемом примере целесообразно составить следующие три уравнения равновесия:
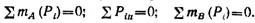
В этом случае в каждое уравнение равновесия войдет только одна искомая реакция:
 |
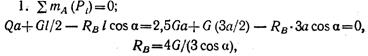
где l cos α — плечо силы RB относительно точки А. Подставляя числовые значения, находим
При определении опорных реакций не было использовано уравнение равновесия ΣPiv = 0. Если реакции определены верно, то сумма проекций на ось v всех сил, действующих на балку, должна быть равна нулю. Проектируя все силы на ось v, получаем
следовательно, реакции определены верно.
Пример 8. Для плоской рамы (рис. 1.16,а) определить опорные реакции.
Дата добавления: 2015-09-07; просмотров: 841;