Проекции и их свойства
1. Предмет и метод инженерной графики. Задачи курса.
2. Центральная проекция и её свойства.
3. Параллельная проекция и её свойства.
4. Аксонометрическая проекция.
5. Комплексный чертёж (Метод Монжа): общие представления.
Комплексный чертёж точки.
1. Предмет и метод инженерной графики. Задачи курса
Учебная дисциплина «Начертательная геометрия и инженерная графика» даёт студентам знания, которые необходимы им для общения с техническими специалистами на специальном графическом языке. Дисциплина включает следующие разделы: начертательную геометрию, машиностроительное черчение, основы компьютерной графики.
В первом семестре мы будем с вами изучать начертательную геометрию, представляющую собой раздел геометрии, в котором пространственные формы предметов действительного мира и соответствующие геометрические закономерности изучаются при помощи изображений на плоскости - чертежей.
Чертёж при этом является инструментом, с помощью которого изучаются геометрические формы предметов, и выполняется решение пространственных задач. Не всякое изображение предмета на листе бумаги позволяет точно определить его геометрическую фигуру.
Для того чтобы чертёж был геометрически равноценным изображаемому предмету, он должен быть построен при помощи метода проецирования (от латинского слова projecere – бросать вперёд). Поэтому чертежи, применяемые в инженерной графике, носят название проекционных чертежей.
Средитребований, предъявляемых к чертежам, наиболее существенными являются:
1) наглядность чертежа (давать пространственное представление изображаемого предмета);
2) обратимость чертежа (по нему можно однозначно воспроизвести форму и размеры изображаемого предмета).
Перед НГ стоят следующие основные задачи:
1) разработка способов построения чертежей пространственных предметов на плоскости;
2) изучение способов решения и исследования пространственных задач при помощи чертежей;
3) развитие пространственного воображения.
В настоящее время чертежи используются практически во всех областях науки и техники. Ни одна, даже самая простая деталь не изготавливается без чертежа. «Чертёж является языком техники», - говорил один из создателей начертательной геометрии французский учёный и инженер Гаспар Монж (11746-1818). Причём этот язык является интернациональным, он понятен любому технически грамотному специалисту, независимо от того, на каком языке он говорит. Дополняя высказывание Монжа, профессор В.И. Курдюмов (1853-1904) – автор классического русского учебника начертательной геометрии - писал: «Если чертёж является языком техники, то начертательная геометрия служит грамматикой этого языка, так как она учит нас правильно читать чужие и излагать наши собственные мысли, пользуясь в качестве слов одними только линиями и точками, как элементами всякого изображения.
2. Центральная проекция и её свойства

 Пусть дана некоторая плоскость П/, которую назовём плоскостью проекций, и вне её т.S, называемая центром проекций (Рис. 1). Для построения проекций некоторой т.А проводят через неё и центр проекций S прямую SA, называемую проецирующей прямой, а затем находят точку пересечения этой прямой с плоскостью П/ - точку A/. Эта точка и называется центральной проекцией точки А на плоскость П/.
Пусть дана некоторая плоскость П/, которую назовём плоскостью проекций, и вне её т.S, называемая центром проекций (Рис. 1). Для построения проекций некоторой т.А проводят через неё и центр проекций S прямую SA, называемую проецирующей прямой, а затем находят точку пересечения этой прямой с плоскостью П/ - точку A/. Эта точка и называется центральной проекцией точки А на плоскость П/.
SA – проецирующая прямая (луч),
A/ - центральная проекция т.А.
Проецирование можно выполнить для любой точки пространства, за исключением точек, лежащих в плоскости, проходящей через центр проекций S и параллельной плоскости проекций П/. За проекции таких точек принято считать бесконечно удалённые точки плоскости П/, которые называются несобственными точками плоскости. И только для центра проекций S проекцию построить нельзя, т.к. проецирующая прямая при этом становится неопределённой.
Если задана какая-либо геометрическая фигура, то проекцией этой фигуры будет являться совокупность проекций всех её точек.
Свойства центрального проецирования:
1) проекцией точки является точка;
2) проекцией прямой линии является прямая линия;
3) проекцией точки, лежащей на некоторой прямой, является точка, лежащая на проекции данной прямой.
Метод центрального проецирования слишком сложен и в значительной степени искажает форму и размеры оригинала, т.к. не сохраняет параллельности прямых и отношения отрезков. Поэтому в технике этот метод не применяется, а используется лишь художниками при написании картин – метод перспективы (глаз человека устроен по принципу центральной проекции).
3. Параллельная проекция и её свойства
Параллельная проекция является частным случаем центральной, когда центр проекций S удалён в бесконечность. В этом случае задаётся направление проецирования, //-но которому проводятся проецирующие лучи.
Пусть дана плоскость проекций П/ и точка А (Рис. 2). Для построения проекции точки проведём через т.А проецирующую прямую // заданному направлению проецирования S. Затем определим точку пересечения этой прямой с плоскостью П/.
 Рис. 2
Рис. 2
| A/ - параллельная проекция т.А. |
Поскольку // проекция является частным случаем центральной, то 3 её свойства распространяются и на //-ую проекцию,
+ свои свойства:
4) проекциями //-ых прямых являются //-ые прямые;
5) отношение проекций отрезков, лежащих на //-ых прямых или на одной и той же прямой, равны отношению самих отрезков;
6) проекция фигуры не меняется при //-ном переносе плоскости проекций.
Эти свойства параллельной проекции обеспечивают более простое построение чертежа, меньше искажающего форму и размеры оригинала по сравнению с центральной проекцией. Так, в связи с сохранением параллельности прямых параллельной проекцией параллелограмма является параллелограмм, а трапеции – тоже трапеция, в то время как в центральной проекции эти фигуры проецируются в четырёхугольники произвольного вида.
В зависимости от величины угла, образованного направлением проецирования S и плоскостью проекций П/ , //-ное проецирование делится на:
1) ортогональное или прямоугольное (90о);
2) косоугольное проецирование.
Ортогональная проекция получила наибольшее распространение в технических чертежах, т.к. она позволяет наиболее легко судить о размерах изображаемых предметов.
Рассмотренные выше методы проецирования однозначно решают прямую задачу – по данному оригиналу построить его проекционный чертёж. Однако обратная задача – по данному проекционному чертежу воспроизвести (реконструировать) оригинал – не решается однозначно. Эта задача допускает бесчисленное множество решений, т.к. точку A/, например, можно считать проекцией любой точки проецирующей прямой, проходящей через т.А. Таким образом, рассмотренные проекционные чертежи не обладают свойством обратимости. Для получения обратимых чертежей нужно дополнить проекционный чертёж необходимыми данными. Существуют различные методы такого дополнения. В данном курсе мы будем рассматривать два вида обратимых чертежей, а именно, аксонометрические и комплексные чертежи в ортогональных проекциях.
4. Аксонометрическая проекция
Название аксонометрическая происходит от древнегреческих слов аксон – ось и метрио - измеряю. Метод аксонометрического проецирования состоит в том, что данная фигура вместе с осями прямоугольной системы координат, которым она отнесена в пространстве, проецируется на некоторую плоскость проекций, называемую аксонометрической плоскостью проекцийиликартинной плоскостью.
В зависимости от вида проецирования аксонометрическая проекция называется:
1) центральной , когда используется центральное проецирование;
2) параллельной, когда используется параллельное проецирование.
Причём в последнем случае аксонометрическая проекция может быть:
а) косоугольной (при косоугольном проецировании);
б) ортогональной (при ортогональном проецировании).
Центральная аксонометрия в нашем курсе не рассматривается и всё, что мы будем говорить далее, касается лишь параллельной и ортогональной проекций.
На Рис. 3 показана схема проецирования т.А на некоторую аксонометрическую плоскость проекций По по направлению проецирования S.
 Рис. 3 Рис. 3
|
OXYZ - натуральная система координат,
OX, OY, OZ - оси натуральной системы координат,
OoXoYoZo - аксонометрическая система координат,
OXo,OYo, OZo - оси аксонометрической системы координат,
ОАхА1А - натуральная координатная ломаная, определяет положение т. А относительно натуральной системы координат OXYZ. Звенья этой ломаной являются отрезками координат.
Длины отрезков координат т.А, измеренные установленной натуральной масштабной единицей е:
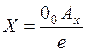
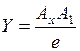
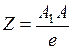 - натуральные координаты т.А
- натуральные координаты т.А
е – натуральная масштабная единица
А0 - аксонометрическая проекция т. А,
00 Ах0 А10 А0 - аксонометрическая координатная ломаная,
ex,ey,ez - аксонометрические масштабные единицы по соответствующим осям координат,
Т.к. при параллельном проецировании сохраняется простое отношение трёх точек, получим:
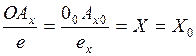
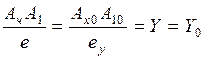
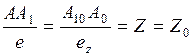
Мы получилиосновное свойство аксонометрических проекций:
Аксонометрические координаты точек, измеренные аксонометрическими масштабами, численно равны натуральным. Таким образом, особенностью рассматриваемого метода аксонометрии заключается в том, что это есть координатный метод построения наглядного однокартинного чертежа, обладающего свойством обратимости.
Для удобства построения аксонометрических чертежей используют показатели искажения – отношения аксонометрического масштаба к соответствующему натуральному масштабу:
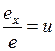 (k);
(k); 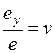 (m);
(m); 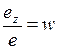 (n).
(n).
В зависимости от величины коэффициентов искажения аксонометрические проекции делятся на:
1) изометрические - u = v = w,
2) диметрические - 2 равны, 3-ий не равен им,
3) триметрические - все 3 коэффициента разные.
Приведём теорему, которая даёт ответ на вопрос, как можно выбрать на чертеже аксонометрические оси и аксонометрические масштабы:
Теорема Польке – Шварца:
3 отрезка произвольной длины, лежащие в одной плоскости и выходящие из одной точки под произвольными углами друг к другу, представляют собой //-ую проекцию 3-х равных отрезков, отложенных на осях прямоугольной системы координат от её начала.
Стандартизовано 5 видов аксонометрических проекций. ГОСТ 2.317-69.
5. Комплексный чертёж (Метод Монжа): общие представления.
Дата добавления: 2015-10-26; просмотров: 2905;
