Следствие.
Теоретические предпосылки определения скоростей и ускорений
Основные формулы для определения скоростей и ускорений точек звеньев механизмов приведены в таблице 3.1.
Планы скоростей и ускорений
Планом скоростей (ускорений) называется диаграмма, на которой от некоторого центра (полюса) в масштабе отложены векторы скоростей (ускорений) точек тела.
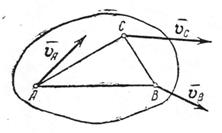
Рассмотрим тело, совершающее плоскопараллельное движение (рис.3.1).
Для плоскопараллельного движения скорости точек определяются по формулам:
, 
, 
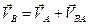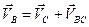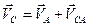(3.1)
где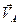 
, 
, 
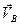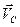- абсолютные скорости точек А, В, С;
, 
, 
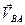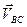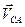- относительные скорости.
План скоростей получим, если в выбранном масштабе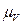 
( 
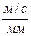) отложим от полюса 
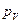отрезк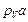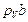и 
, 
и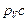 
, параллельные векторам скоростей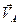 
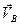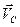, , . Отрезки находятся по формулам: 
, 
, 
.
|
|
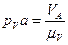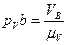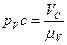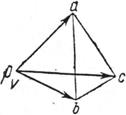
В результате построения плана скоростей получен треугольник авс (рис.3.2),который подобен треугольнику АВС. Относительных скоросте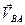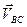й , и 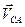находятся по формулам: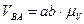 
, 
.
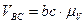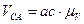Рис.3.1 Рис.3.2
Сформулируем принцип подобия в плане скоростей:
В плане скоростей векторы относительных скоростей точек жесткого звена образуют фигуру, подобную звену, повернутую на угол 90° в сторону угловой скорости звена.
Следствие.
Пользуясь принципом подобия, достаточно на плане скоростей построить векторы скоростей только двух точек жесткого звена. Скорость же любой третьей точки определится путем построения фигуры или линии подобной данному звену.
Аналогично формулируется принцип подобия в плане ускорений.
Дата добавления: 2015-10-21; просмотров: 434;