Решение. Момент инерции сечения вычисляем как раз­ность моментов инерции большого и малого прямоуголь­ников

Момент инерции сечения вычисляем как раз­ность моментов инерции большого и малого прямоуголь­ников

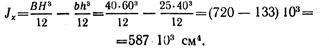
Осевоймомент сопротивления

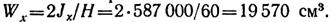
Допускаемый изгибающий момент определяем из расчета по наибольшим растягивающим напряжениям

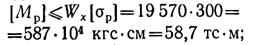
то же, по наибольшим сжимаю­щим напряжениям

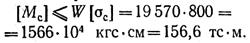
Меньший из вычисленных моментов [М_р] = 58,7 тс-м опре­деляет допускаемую нагрузку балки.

Таким образом, в чугунной балке симметричного сече­ния допускаемая нагрузка ограничивается прочностью растянутых волокон. Чтобы для чугунной балки допускае­мая нагрузка была одинакова по условиям прочности растянутых и сжатых волокон, сечение ее должно быть несимметричным относительно нейтральной оси. Расстоя­ния от нейтральной оси до крайних волокон растянутой зоны у_р и сжатой у_с должны удовлетворять отношению

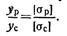
Этого можно добиться, в частности, применив несимметричный двутавр, у которого горизонтальная полка, находящаяся в растянутой зоне, толще, чем полка, расположенная в сжатой зоне.

Контрольные вопросы и задания

1. Напишите формулу для определения нормального напряже­ния при изгибе в любой точке поперечного сечения.

2. Нормальное напряжение в точке В поперечного сечения 120МПа. Определите напряжение в точке С (рис. 32.11).

3. В каком случае (рис. 32.12) балка выдержит большую нагрузку?

4. Напишите формулы для определения момента инерции и мо­мента сопротивления для прямоугольника. Что характеризуют эти величины? Укажите единицы измерения этих величин.

5. Напишите условие прочности при изгибе.

6. Определите изгибающий момент в точке В (рис. 32.13), ис­пользуя метод характерных точек.