Преобразования Галилея
Инерциальные системы отсчета. Принцип относительности Галилея.
Рассмотренные ранее переходы от декартовой к сферической, цилиндрической или другой системе координат относятся к одной и той же системе отсчета. Это простые геометрические преобразования.
Связь систем отсчета, находящихся в движении относительно друг друга, это физическая задача.
Система отсчета, движущаяся поступательно равномерно и прямолинейно, называется инерциальной системой отсчета. В инерциальных системах отсчета выполняются законы инерции Ньютона.
Из многочисленных экспериментов известно, что в инерциальных системах координат все механические явления протекают одинаково – это постулат относительности Галилея (Галилео Галилей, 1564 – 1642, Италия).
Это постулат, т.к.:
- подтверждается физическими экспериментами, которые являются точными;
- «все» явления еще не открыты;
Преобразования Галилея

В момент t=0 начала систем отсчета совпадают, а в момент t K’ находится в точке 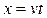
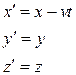
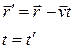 преобразования Галилея
преобразования Галилея
Пусть не штрихованная система движется относительно штрихованной системы со скоростью 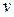 . Тогда:
. Тогда:
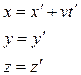
Величины, численные значения которых не изменяются при преобразованиях – инварианты. При преобразованиях изменяются варианты (скорость, импульс, координаты).
Рассмотрим, как ведет себя длина тел при преобразованиях Галилея.
Пусть в штрихованной системе находится стержень с координатами
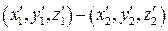
Его длина в неподвижной системе отсчета:
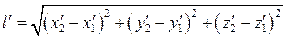
В движущейся системе отсчета: засекли концы движущегося стержня одновременно. Длина движущегося стержня:
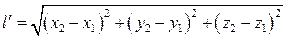
Воспользуемся формулами преобразования Галилея:
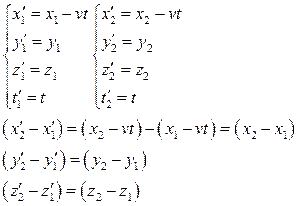
- Поскольку
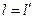 , то длина тела – инвариант.
, то длина тела – инвариант. - При выводе преобразований Галилея считаем, что время абсолютно и неизменно для всех систем отсчета. Это интуитивное предположение примем без доказательства. В классической механике оно считалось естественным, само собой разумеющимся.
- Одновременность двух событий имеет абсолютный характер, независимый от системы отсчета. Отсюда вытекает инвариант времени:
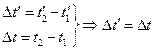
Дата добавления: 2015-10-21; просмотров: 1069;
