Доверительные интервалы для оценки среднего квадратичного отклонения нормальной случайной величины

Асимметрия характеризует несимметричность плотности (или закона распределения) случайной величины X относительно ее математического ожидания

Эксцессом случайной величины X называется число

.

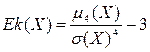Можно доказать, что асимметрия и эксцесс нормальной случайной величины равны нулю. Асимметрия и эксцесс характеризуют общие свойства графика плотности и не меняются при прибавлении к величине X постоянной или умножении Х на постоянную.

Рассмотрим теперь оценки указанных выше теоретических моментов, асимметрии и эксцесса.

Начальным эмпирическим моментом k-го порядка полученным по результатом выборки ( 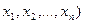случайной величины Х называется следующая оценка ее соответствующего начального момента

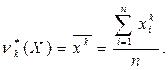
Центральным эмпирическим моментом k-го порядка называется оценка соответствующего центрального момента величины Х

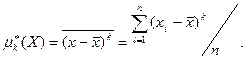
Связь между этими начальными и центральными моментами аналогична соотношениям между соответствующими теоретическими величинами:

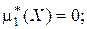
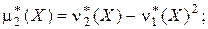
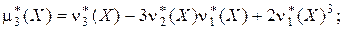
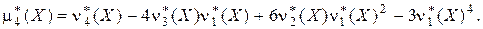
Эмпирической асимметрией называется оценка

.

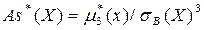Эмпирическим эксцессом называется оценка

.

Можно доказать, что при больших объемах выборки n все эти оценки можно считать несмещенными и эффективными, оценки состоятельны.

Выводы. По данной теме нами были рассмотрены точечные оценки параметров случайных величин, требования к оценкам, выборочная средняя, выборочная дисперсия и исправленная выборочная дисперсия. Рассмотрены также моменты и выборочные моменты случайной величины, асимметрия и эксцесс.

Лекция №21-22. Метод моментов для оценки параметров случайной величины. Метод максимального правдоподобия. Доверительные интервалы.

План. Метод моментов для оценки параметров случайных величин. Метод максимального правдоподобия для оценки параметров случайных величин. Интервальные оценки, точность и надежность. Доверительные интервалы для оценок математического ожидания и дисперсии нормальной случайной величины.

3.5. Метод моментов для оценки параметров случайных величин

Рассмотрим теперь один из методов, позволяющий получать оценки неизвестных параметров плотности (или закона распределения) случайной величины Х. Пусть известен общий вид плотности Х 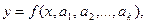где - неизвестные значения параметров и пусть - выборка этой величины. Найдем первый начальный и центральные моменты величины Х до k-го порядка включительно:

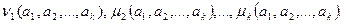
Эти величины являются функциями от k параметров. По результатам выборки вычислим оценки этих моментов и приравняем их к соответствующим теоретическим моментам, получим систему из k уравнений с k неизвестными:

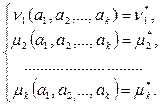
Решение этой системы - числа 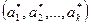и будут являться оценками соответствующих параметров.

3.6. Метод максимального правдоподобия для оценки параметров случайных величин

Рассмотрим еще один метод, позволяющий находить оценки параметров 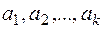плотности непрерывной случайной величины Х по результатам ее выборки объема n: 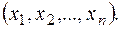С помощью этого метода можно находить также оценки параметров 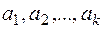вероятностей 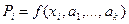дискретной величины Х по результатам ее выборки объема n: 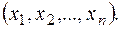Функцией правдоподобия для указанных случайных величин и выборок называется следующая функция k переменных

.

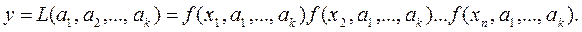В этом методе в качестве оценки параметров 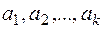берутся значения 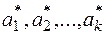при которых функция 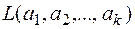достигает своего максимума. Эта оценка и называется оценкой максимального правдоподобия.

Часто вместо нахождения максимума функции L находят максимум ее логарифма - функции 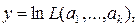поскольку эти две функции достигают своих экстремумов в одних и тех же точках. Практически для нахождения указанного экстремума необходимо решить систему и k уравнений с k неизвестными

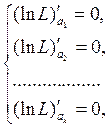
а затем исследовать полученное решение с помощью достаточного условия экстремума.

§4. Интервальные оценки параметров случайных величин

Точечные оценки параметров случайных величин не вполне полноценны, поскольку они не содержат информацию о погрешности такой оценки. Более логично пользоваться оценкой в виде интервала, в который с определенной вероятностью может попадать оцениваемая величина. Пусть A - неизвестный параметр случайной величины X и пусть 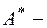некоторая его точечная оценка. Доверительным интервалом называется интервал вида 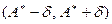с центром в точке 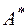. Число δ здесь называется точностью (или погрешностью) этой оценки. Вероятность того, что параметр A попадает в свой доверительный интервал, называется надежностью этой оценки:

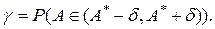
Требования к качеству точности δ и надежности γ противоречивы, т.е. при повышении надежности ухудшается (увеличивается) точность. Практически число 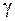задается заранее исходя из поставленной задачи, а затем по нему определяется число δ.

4.1. Доверительные интервалы для оценки математического ожидания нормальной случайной величины при известном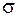

Пусть имеется выборка объема n нормальной случайной величины X с неизвестным математическим ожиданием и известным СКО , надежность задана. Выборочное среднее является точечной оценкой математическое ожидания а, поэтому является центром искомого интервала.

Теорема. Доверительный интервал для оценки математического ожидания нормальной случайной величины по её выборке объёма n при известном 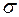и заданной 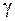имеет вид 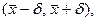где 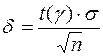. Здесь есть решение уравнения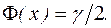

Последнее уравнение можно приближенно решить с помощью таблицы интегральной функции Лапласа .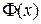

С помощью таких интервалов оценивается истинное значения измеряемой величины а по результатам n ее измерений прибором, средняя погрешность 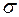которого известна.

4.2. Доверительные интервалы для оценки математического ожидания нормальной случайной величин при неизвестном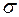

Для решения этой задачи используется следующая случайная величина. Пусть и 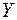независимые нормированные нормальные случайные величины. Распределением Стьюдента с k степенями свободы называется случайная величина

.

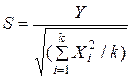Плотность этой величины четная функция; при 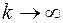стьюдентовская величина S стремится к нормированной нормальной величине.

Известно, что если 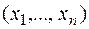есть выборка некоторой нормальной случайной величины с математическим ожиданием а по результатам которой вычислены 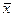и исправленная СКО s, то величина 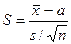является распределением Стьюдента с 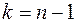степенями свободы.

Теорема. Доверительный интервал для оценки математического ожидания нормальной случайной величины по её выборке объёма n для заданной надежности 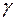имеет вид 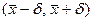, где

Здесь s – исправленное СКО, 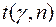- решение уравнения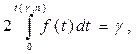 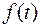- плотность Стьюдентовской величины с 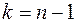степенями свободы. Значения 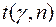можно получить из таблицы.

Такие доверительные интервалы применяются для оценки истинного значения измеряемой величины 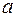при неизвестной точности прибора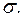

Замечание. При больших 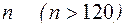можно воспользоваться предыдущим методом п. 3.7.1, считая, что 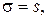поскольку при этих n распределение Стьюдента мало отличается от нормированной нормальной случайной величины.

Доверительные интервалы для оценки среднего квадратичного отклонения нормальной случайной величины

Такой доверительный интервал может быть записан в виде 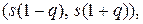где s - исправленное выборочное СКО найденное по результатам выборки объема n, а q в зависимости от 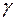и n находится таблице.

Заметим, что поскольку СКО всегда положительно, то при 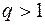в качестве левой границы интервала берется 0.

Эти интервалы используются для оценки неизвестной точности прибора 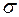по результатам n измерений некоторой величины этим прибором.

Выводы.По данной теме нами были рассмотрены метод моментов для оценки параметров случайных величин и метод максимального правдоподобия для оценки параметров случайных величин. Введены понятия интервальной оценки параметров случайных величин, точности и надежности. Рассмотрены доверительные интервалы для оценок математического ожидания и дисперсии случайной величины.