Полный факторный эксперимент.
Исходные данные (пример):
1. Диапазон количества вагонов в составе 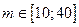 .
.
2. Диапазон длины полурейса 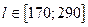 .
.
3. Нормативы времени при длине полурейса (табл. 5.1):
Таблиця 5.1
| от | до | a | b |
| 0,90 | 0,018 | ||
| 1,00 | 0,020 | ||
| 1,10 | 0,022 |
Определить:функцию отклика 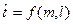 .
.
Решение:
Для того, чтобы установить зависимость функции отклика от двух факторов 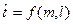 (фактор 1 – количество вагонов (
(фактор 1 – количество вагонов (  ), фактор 2 – длина полурейса (
), фактор 2 – длина полурейса ( 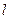 )) необходимо рассмотреть влияние каждого фактора на двух уровнях, то есть выполнить N=22=4 опыта.
)) необходимо рассмотреть влияние каждого фактора на двух уровнях, то есть выполнить N=22=4 опыта.
Общий вид функции отклика, зависящей от двух факторов приведен ниже:
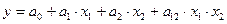 , (5.1)
, (5.1)
или, для условия данной задачи
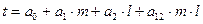
Функция отклика в зависимости от уровней значений факторов имеет следующий вид:
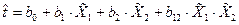 , (5.2)
, (5.2)
Рассчитаем значение функции 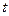 при разных уровнях значений каждого фактора.
при разных уровнях значений каждого фактора.
Найдем значение 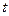 за формулой:
за формулой:
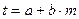 , (5.3)
, (5.3)
Значения факторов, а также расчетное значение 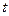 в каждом опыте приведены ниже:
в каждом опыте приведены ниже:
Опыт 1: фактор 1, нижний уровень –  = 10 ваг,
= 10 ваг,
фактор 2, нижний уровень – 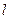 = 170 м.
= 170 м.
По длине полурейса определяем коэффициенты 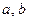 и, подставив их в выражение 5.3, получим:
и, подставив их в выражение 5.3, получим:
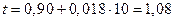 хв
хв
Опыт 2: фактор 1, нижний уровень –  = 10 ваг,
= 10 ваг,
фактор 2, верхний уровень – 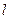 = 290 м.
= 290 м.
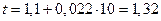 хв
хв
Опыт 3: фактор 1, верхний уровень –  = 40 ваг,
= 40 ваг,
фактор 2, нижний уровень – 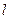 = 170 м.
= 170 м.
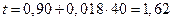 хв
хв
Опыт 4: фактор 1, верхний уровень –  = 40 ваг,
= 40 ваг,
фактор 2, верхний уровень – 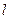 = 290 м.
= 290 м.
 хв
хв
Выполним расчеты в табличной форме (табл. 5.2) для поиска коэффициентов уравнения 5.2:
Таблица 5.2
| Опыт | 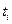
| 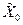
| 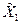
| 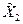
| 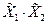
| 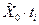
| 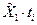
| 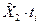
| 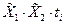
| 
|
| 1.08 | +1 | –1 | –1 | +1 | +1.08 | –1.08 | –1.08 | +1.08 | 1.08 | |
| 1.32 | +1 | –1 | +1 | –1 | +1.32 | –1.32 | +1.32 | –1.32 | 1.32 | |
| 1.62 | +1 | +1 | –1 | –1 | +1.62 | +1.62 | –1.62 | –1.62 | 1.62 | |
| 1.98 | +1 | +1 | +1 | +1 | +1.98 | +1.98 | +1.98 | +1.98 | 1.98 | |
| Итого | 6.00 | 1.20 | 0.60 | 0.12 |
В этой таблице 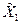 та
та 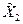 определяют уровни, соответственно, первого и второго факторов, причем, при нижнем уровне значения фактора
определяют уровни, соответственно, первого и второго факторов, причем, при нижнем уровне значения фактора 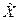 = –1, а при верхнем уровне
= –1, а при верхнем уровне 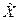 = +1.
= +1.
Исходя из таблицы, определяем коэффициенты уравнения (проведено N=4 опыта):
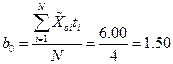 ,
,
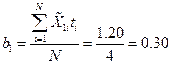 ,
,
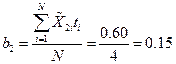 ,
,
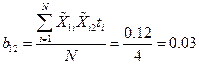 .
.
С учетом найденных коэффициентов уравнение функции отклика приобретет следующий вид:
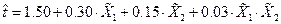 (5.4)
(5.4)
Проверим адекватность полученной зависимости. Для этого найдем значения факторов на среднем уровне:
 ваг,
ваг,
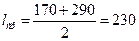 м,
м,
Рассчитаем продолжительность полурейса среднего состава на среднее расстояние:
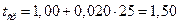 хв
хв
Функция отклика при нулевых уровнях двух факторов будет равна:
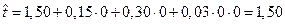 хв
хв
Сравнивая полученные результаты (1,50=1,50), делаем вывод об адекватности зависимости (5.2).
Для получения аналитической зависимости между функцией отклика и действительными значениями указанных факторов выполним некоторые преобразования:
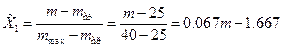 , (5.5)
, (5.5)
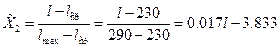 . (5.6)
. (5.6)
Тогда функция отклика будет иметь следующий вид
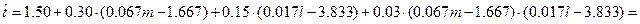

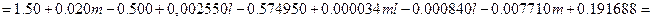

Таким образом
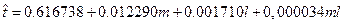 , (5.7)
, (5.7)
Выводы:
1. Поскольку коэффициенты 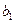 и
и 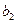 положительные, следовательно между функцией отклика и двумя факторами прямопропорциональная связь, то есть, увеличение какого-либо из факторов приведет к увеличению и функции отклика
положительные, следовательно между функцией отклика и двумя факторами прямопропорциональная связь, то есть, увеличение какого-либо из факторов приведет к увеличению и функции отклика  .
.
2. Сравнивая рассчитанные коэффициенты 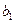 и
и 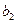 друг с другом, можно отметить, что коэффициент
друг с другом, можно отметить, что коэффициент 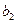 =0.15 в два раза меньше коэффициента
=0.15 в два раза меньше коэффициента 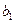 =0.30, из чего следует, что большее влияние на функцию отклика имеет первый фактор, то есть число вагонов.
=0.30, из чего следует, что большее влияние на функцию отклика имеет первый фактор, то есть число вагонов.
3. Следует обратить внимание на незначительное влияние двух факторов вместе, о чем говорит коэффициент 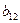 =0.03.
=0.03.
4. Проведенная выше проверка функции отклика позволяет, согласно полученным результатам, говорить о ее полной адекватности.
5. Выражение 5.6 для функции типа  позволяет, подставляя действительные значения факторов (из указанных в задании диапазонов), получить значения функции отклика.
позволяет, подставляя действительные значения факторов (из указанных в задании диапазонов), получить значения функции отклика.
| <== предыдущая лекция | | | следующая лекция ==> |
| Гиповитаминоз фолиевой кислоты (Hypovitaminosis Вс), (гипофолиоз, Hypoacidofoliosus) | | | Система животного мира. 1 страница |
Дата добавления: 2015-10-19; просмотров: 669;
