Критерий устойчивости Михайлова
Так как для устойчивой САУ число правых корней m = 0, то угол поворота вектора D(j  ) составит
) составит
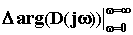 = n
= n  /2.
/2.
То есть САУ будет устойчива, если вектор D(j  ) при изменении частоты
) при изменении частоты  от 0 до +
от 0 до + 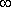 повернется на угол n
повернется на угол n  /2.
/2.
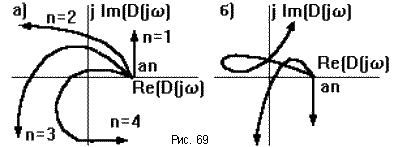
При этом конец вектора опишет кривую, называемую годографом Михайлова. Она начинается на положительной полуоси, так как D(0) = an, и последовательно проходит против часовой стрелки n квадрантов комплексной плоскости, уход в бесконечность в n - ом квадранте (рис.69а).
Если это правило нарушается (например, число проходимых кривой квадрантов не равно n, или нарушается последовательность прохождения квадрантов (рис.69б)), то такая САУ неустойчива - это и есть необходимое и достаточное условие критерия Михайлова.
Достоинства. Этот критерий удобен своей наглядностью. Так, если кривая проходит вблизи начала координат, то САУ находится вблизи границы устойчивости и наоборот. Этим критерием удобно пользоваться, если известно уравнение замкнутой САУ.
Для облегчения построения годографа Михайлова выражение для D(j  ) представляют суммой вещественной и мнимой составляющих:
) представляют суммой вещественной и мнимой составляющих:
D(j  ) = a0(j
) = a0(j  - p1)(j
- p1)(j  - p2)...(j
- p2)...(j  - pn) = a0(j
- pn) = a0(j  )n + a1(j
)n + a1(j  )n - 1 + ... + an = ReD(j
)n - 1 + ... + an = ReD(j  ) + jImD(j
) + jImD(j  ),
),
где
ReD(j  ) = an - an - 2
) = an - an - 2  2 + an- 4
2 + an- 4  4 - ...,
4 - ...,
ImD(j  ) = an - 1
) = an - 1  - an - 3
- an - 3  3 + an- 5
3 + an- 5  5 - ....
5 - ....
Меняя  от 0 до
от 0 до 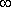 по этим формулам находят координаты точек годографа, которые соединяют плавной линией.
по этим формулам находят координаты точек годографа, которые соединяют плавной линией.
Дата добавления: 2015-10-19; просмотров: 602;
