ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ

Если обкладки заряженного конденсатора замкнуть металлической про­волокой, то в ней возникает электрический ток, а конденсатор разрядится. Электрический ток разряда конденсатора выделяет в проволоке определённое количество тепла, а это значит, что заряженный конденсатор обладает энергией.

Вычислим энергию заряженного конденсатора С. Для этого обозначим через U мгновенное значение напряжения на обкладках конденсатора в процессе разряда. Если малое количество заряда dq проходит в процессе разряда с одной обкладки на другую, то работа электрических сил dА будет

dА =U dq.

Выражая в этой формуле заряд обкладок qчерез напряжение

Q = CU, получим

dA = CU dU.

Полную работу, совершаемую электрическими силами за все время разряда, равную энергии кон­денсатора W, мы получим, интегрируя это выражение между значениями напряжения U (начало разряда) и 0 (конец разряда). Это дает:

A= - W = C 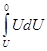= - CU²/2. (1)

Можно (1) переписать:

W = CU²/2 = q²/2C = qU/2. (2)

А где именно, т.е. в каком месте в конденсаторе локализована эта энергия? - На об­кладках конденсатора, т.е. на электрических зарядах, или в его электрическом поле, т.е. в пространстве между обкладками. В дальнейшем мы сможем ответить на этот вопрос, что энергия сосредоточена в электрическом поле.Дальнейшее развитие теории и эксперимента показало, что переменные во времени электрические и магнитные поля могут существовать обособленно, независимо от возбудивших их зарядов, и распространяются в пространстве в виде электромагнитных волн, способных переносить энергию.

Учитывая это, мы можем преобразовать (2) т.о., чтобы в него входила характеристи­ка поля - его напряженность.

Рассмотрим вначале однородное поле и применим формулу (1) к плоскому конденсатору. Мы получим

W = ee₀SU²/2d = ee₀(U/d)²Sd/2, но

U/d=E, a Sd - объём, занимаемый полем.

Мы видим, что энергия однородного электрического поля пропорциональна объёму, занимаемому полем. Поэтому целесообразно говорить об энергии каждой единицы объёма, или об объёмной плотности энергии электрического поля.Она равна

W₁ = ee₀E²/2 = ED/2, т.к. V = Sd = 1.

Последнее выражение справедливо только для изотропного диэлектрика.

Если электрическое поле неоднородно, то его можно разбить на элементарные объемы dV и считать, что в пределах бесконечно малого объема это поле однородно. Поэтому энергия, заключенная в объеме поля dV, будет W₁dV, а полная энергия любого электрического поля может быть представлена в виде

W = (e₀/2) dV,

Причем интегрирование проводится по всему объему V, где имеется электрическое поле.