СИЛЫ ТРЕНИЯ.

Опыт показывает, что всякое тело, движущееся по горизонтальной поверхности другого тела и предоставленное самому себе, с течением времени замедляет свое движение и наконец останавливается. Это значит, что на него со стороны другого тела, по поверхности которого оно движется, действует сила, направленная противоположно его скорости и наз. силой трения.О наличии сил трения свидетельствует и тот факт, что для приведения в движение тела, лежащего на поверхности другого тела, к нему необходимо приложить конечную силу, направленную в сторону движения и превышающую некоторую определенную минимальную величину. Эта сила необходима для преодоления силы трения покоя, препятствующей движению.

`F_тр

FFF

Рис.1

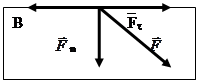
Силу `F, действующую со стороны тела А на соприкасающееся с ним тело В, можно разложить на составляющие `F_n и `F_t (рис.1):

`F = `F_t + `F_n (1).

Составляющая `F_t лежит в плоскости соприкасающихся тел и зависит от состояния и свойств соприкасающихся поверхностей. Эта составляющая и вызывает силу трения.

Т.о., силы трения – это силы, действующие между телами вдоль их соприкасающихся поверхностей как при покое, так и при относительном движении тел и зависящие от состояния и свойств поверхностей соприкосновения, а также от их относительной V.При этом сила трения, действующая на тело, всегда направлена противоположно его скорости по отношению к другому телу, соприкасающемуся с ним. Силы трения возникают при действии на соприкасающиеся тела внешних сил, имеющих составляющие, направленные вдоль поверхности соприкосновения, а также при движении этих тел относительно друг друга.

Силы трения действуют на оба соприкасающихся тела, будучи равными по величине и противоположно направленными, причем их направления противоположны относительным скоростям тел. Так, пусть тело А (Рис.2) движется со скоростью `V_A по

j _А `V_A

`j_В

Рис.2.

поверхности другого тела В, скорость которого `V<sub>B</sub>, направлена в ту же сторону, но |V<sub>B</sub>| < |V<sub>A</sub>|. Относительная скорость тела А (по отношению к условно неподвижному телу В) равна `V_A - `V<sub>В</sub> и направлена, как и `V_A. Поэтому сила трения j_А, действующая на него со стороны тела В, будет направлена противоположно его относительной скорости (влево). Относительная же скорость тела В равна `V<sub>B</sub> - `V_A и направлена в сторону противоположную `V<sub>A</sub> (т.к. V<sub>B</sub> < V<sub>A</sub>). Поэтому сила трения j<sub>В</sub> будет действовать на тело В в направлении его скорости `V_B (вправо).

Силы трения, действуя на тело, как и всякие другие силы, влияют на характер движения, поэтому их тоже необходтмо учитывать. В частности, чтобы поддерживать скорость движущегося тела `V неизменной, на него необходимо все время действовать с силой `F, направленной в сторону движения и по величине равной силе трения `j,препятствующей движению. Тогда эти две силы уравновесят др. др. и ускорение тела

d`V/dt = (`F + `j)/m = 0 , т.к. `F + `j = 0.

В действительности тела движутся равномерно и прямолинейно не тогда, когда на них никакие силы не действуют (это невозможно осуществить в земных условиях), а когда силы трения уравновешиваются другими, противоположно направленными силами, приложенными к телу извне.

Чтобы измерить силу трения `j, действующую на некоторое тело массы m , к нему прилагают известную (измеримую непосредственно) движущую силу `F, подобрав ее величину такой, чтобы тело двигалось без ускорения. Тогда по 2-му закю Ньтона:

`F +`j =md`V/dt = 0 ® `j =`F.

В частности, для измерения силы трения `j применяется такой метод, рис. 3.

`T <sup>¢</sup> m `j

`T

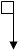M

M`g Рис.3.

Груз M подбирают таким, чтобы тело двигалось без ускорения. В этом случае j = Т = Mg.

Прибор для измерения сил трения называется трибометром.

Силы трения, действуют между соприкасающимися твердыми телами, наз. силами сухого трения. Они действуют и при движении соприкасающихся тел и при их относительном покое. Характерной особенностью, отличающей их от трения в жидкостях и газах, является то, что по мере уменьшения относительной скорости соприкасающихся тел вплоть до нуля силы сухого трения, действующие между ними, не обращаются в нуль, а стремятся к определенной величине, наз.трением покоя.Рассказать о силе трения покоя по рис.3.

При стремлении сдвинуть одно тело по поверхности другого в плоскости соприкосновения тел возникает сила трения покоя, величина которой может меняться от 0 до j_пред, называется предельной силой трения. Сила трения покоя – неоднозначная величина: с изменением внешней силы соотв. изменяется и сила трения покоя так, чтобы уравновесить внешнюю силу. Когда внешняя сила окажется по величине больше `j_пред, то возникнет скольжение данного тела по поверхности соприкасающегося с ним другого тела.

Опыт показывает, что силы трения зависят от относительной скорости скольжения. Вначале с возрастанием относительной скорости величина j несколько уменьшается, а затем при дальнейшем увеличении скорости, величина j медленно начинает возрастать. Но эти изменения слабые, так что часто считают, что j не зависит от скорости. j зависит от материала, от состояния соприкасающихся поверхностей (от их шероховатости), а также от величины силы нормального давления одного из данных тел на другое.Кулон исследовал силы трения и установил закон Кулона :

Величина сил тренияj, действующих между двумя данными телами, не зависит от площади их соприкасающихся поверхностей и пропорциональна силе нормального давленияN:

j = kN , где

к – коэф. трения скольжения, N – сила нормального давления.

j_пред = к₀ N, где

к₀ – коэф. трения покоя. k > k₀. Коэф. трения в таблицах.

Силы трения действуют и при качении тела по поверхности другого тела. В этом случае

j = SN/R, где

R – радиус катящегося тела, S – коэффициент трения качения.

Обычно S/R <<k ! ® замена скольжения тела его качением.Для уменьшения трения между трущимися поверхностями твердых тел помещают смазку, т.к. внутренее трение жидкости меньше трения скольжения.

8.СИЛЫ УПРУГОСТИ. ЗАКОН ГУКА.

Силы упругости – это силы, возникающие только при деформации тел. Действующая на тело сила может деформировать тело, составляющие его частицы смещаются друг относительно друга. При этом в соответствии с 3-м законом Ньютона внутри деформированного тела возникает противодействующая сила, равная по модулю деформирующей силе и называемая силой упругости. При прекращении деформации силы упругости исчезают.

Пример: растяжение пружины или резинки.

Заметим, что хотя силы упругости появляются только при деформациях, но не всегда деформация приводит к появлению сил упругости. Силы упругости возникают в телах, которые восстанавливают свою форму или объем после прекращения действия сил, вызывающих деформацию. Именно такие силы называются упругими.

Деформация называется упругой,если после прекращения внешнего воздействия тело полностью восстанавливает свою форму и размеры. При пластической деформацииизменения размеров и формы тела полностью не исчезают после прекращения действия силы. Мы будем рассматривать только упругую деформацию.

Существует несколько видов деформации тел: одностороннее растяжение или сжатие, всестороннее растяжение или сжатие, кручение, сдвиг, изгиб. Каждый вид деформации вызывает появление соответствующие силы упругости.

Английский физик Роберт Гук установил экспериментальную зависимость между силой упругости и величиной деформации: сила упругости `F, возникающая при малых деформациях любого вида, пропорциональна деформации DX(закон Гука)

`F = - k D`X.

При больших смещениях DX возникает остаточная деформация –тело не восстанавливает полностью свои форму и размер. При значительных деформациях может даже произойти разрушение тела (рис.) Этот закон легко установить, наблюдая растяжение пружины под действием силы `F, приложенной к ее концу.

`F

DХ

Рис.1.

Легко установить, что |F_упр| = k |DX|. Коэф. k –наз. коэф. упругостиили жесткостью пружины. Коэффициент k различных тел зависит от формы и материала вещества, в котором возникают силы упругости.

При растяжении и сжатии стержней из стали, чугуна и т.д. уменьшение или увеличение их длины также пропорционально приложенной силе. Величина k для стержней зависит не только от материала стержня, но и от его начальной длины l₀ и площади поперечного сечения S. Эта зависимость отражается следующей формулой:

K = SE/l₀,

где Е – называется модулем упругости материала или модулем Юнга, он характеризует упругие свойства вещества стержня и не зависит от размеров тела. Сила же упругости для стержня будет F_упр = SEDl /l₀ ,

откуда при Dl = l₀ и S = 1 получим Е = F_упр, т.е