Получение синусоидальной ЭДС. . Основные характеристики синусоидального тока

Основным преимуществом синусоидальных токов является то, что они позволяют наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Целесообразность их использования обусловлена тем, что коэффициент полезного действия генераторов, электрических двигателей, трансформаторов и линий электропередач в этом случае оказывается наивысшим.

Для получения в линейных цепях синусоидально изменяющихся токов необходимо, чтобы э. д. с. также изменялись по синусоидальному закону. Рассмотрим процесс возникновения синусоидальной ЭДС. Простейшим генератором синусоидальной ЭДС может служить прямоугольная катушка (рамка), равномерно вращающаяся в однородном магнитном поле с угловой скоростью ω (рис. 2.1, б).

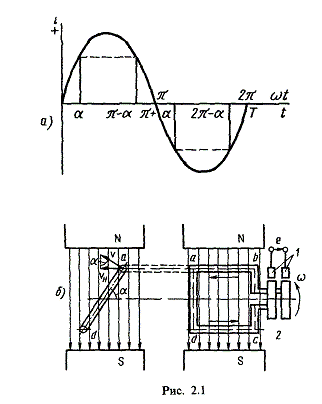
Пронизывающий катушку магнитный поток во время вращения катушки abcd наводит (индуцирует) в ней на основании закона электромагнитной индукции ЭДС е. Нагрузку подключают к генератору с помощью щеток 1, прижимающихся к двум контактным кольцам 2, которые, в свою очередь, соединены с катушкой. Значение наведенной в катушке abcd э. д. с. в каждый момент времени пропорционально магнитной индукции В, размеру активной части катушки l = ab + dc и нормальной составляющей скорости перемещения ее относительно поля v_н:

e = Blv_н (2.1)

где В и l - постоянные величины, a v_н - переменная, зависящая от угла α. Выразив скорость v_н через линейную скорость катушки v, получим

e = Blv·sinα (2.2)

В выражении (2.2) произведение Blv = const. Следовательно, э. д. с., индуцируемая в катушке, вращающейся в магнитном поле, является синусоидальной функцией угла α.

Если угол α = π/2, то произведение Blv в формуле (2.2) есть максимальное (амплитудное) значение наведенной э. д. с. E_m = Blv. Поэтому выражение (2.2) можно записать в виде

e = E_msinα (2.3)

Так как α есть угол поворота за время t, то, выразив его через угловую скорость ω, можно записать α = ωt, a формулу (2.3) переписать в виде

e = E_msinωt (2.4)

где е - мгновенное значение э. д. с. в катушке; α = ωt - фаза, характеризующая значение э. д. с. в данный момент времени.

Необходимо отметить, что мгновенную э. д. с. в течение бесконечно малого промежутка времени можно считать величиной постоянной, поэтому для мгновенных значений э. д. с. е, напряжений и и токов i справедливы законы постоянного тока.

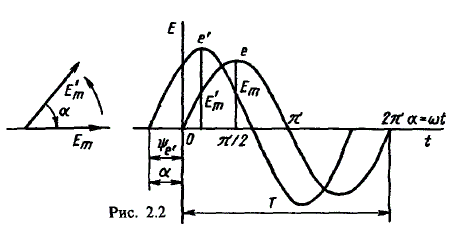
Синусоидальные величины можно графически изображать синусоидами и вращающимися векторами. При изображении их синусоидами на ординате в определенном масштабе откладывают мгновенные значения величин, на абсциссе - время. Если синусоидальную величину изображают вращающимися векторами, то длина вектора в масштабе отражает амплитуду синусоиды, угол, образованный с положительным направлением оси абсцисс, в начальный момент времени равен начальной фазе, а скорость вращения вектора равна угловой частоте. Мгновенные значения синусоидальных величин есть проекции вращающегося вектора на ось ординат. Необходимо отметить, что за положительное направление вращения радиус-вектора принято считать направление вращения против часовой стрелки. На рис. 2.2 построены графики мгновенных значений э. д. с. е и е'.

Если число пар полюсов магнитов p ≠ 1, то за один оборот катушки (см. рис. 2.1) происходит p полных циклов изменения э. д. с. Если угловая частота катушки (ротора) n оборотов в минуту, то период уменьшится в pn раз. Тогда частота э. д. с., т. е. число периодов в секунду,

f = Pn / 60

Из рис. 2.2 видно, что ωТ = 2π, откуда

ω = 2π / T = 2πf (2.5)

Величину ω, пропорциональную частоте f и равную угловой скорости вращения радиус-вектора, называют угловой частотой. Угловую частоту выражают в радианах в секунду (рад/с) или в 1 / с.

Графически изображенные на рис. 2.2 э. д. с. е и е' можно описать выражениями

e = E_msinωt; e' = E'_msin(ωt + ψ_e').

Здесь ωt и ωt + ψ_e' - фазы, характеризующие значения э. д. с. e и e' в заданный момент времени; ψ_e' - начальная фаза, определяющая значение э. д. с. е' при t = 0. Для э. д. с. е начальная фаза равна нулю (ψ_e = 0). Угол ψ всегда отсчитывают от нулевого значения синусоидальной величины при переходе ее от отрицательных значений к положительным до начала координат (t = 0). При этом положительную начальную фазу ψ (рис. 2.2) откладывают влево от начала координат (в сторону отрицательных значений ωt), а отрицательную фазу - вправо.

Если у двух или нескольких синусоидальных величин, изменяющихся с одинаковой частотой, начала синусоид не совпадают по времени, то они сдвинуты друг относительно друга по фазе, т. е. не совпадают по фазе.

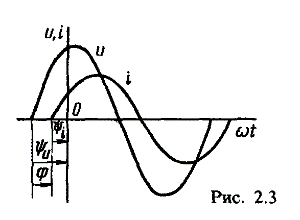
Разность углов φ, равная разности начальных фаз, называют углом сдвига фаз. Сдвиг фаз между одноименными синусоидальными величинами, например между двумя э. д. с. или двумя токами, обозначают α. Угол сдвига фаз между синусоидами тока и напряжения или их максимальными векторами обозначают буквой φ (рис. 2.3).

Когда для синусоидальных величин разность фаз равна ±π, то они противоположны по фазе, если же разность фаз равна ±π/2, то говорят, что они находятся в квадратуре. Если для синусоидальных величин одной частоты начальные фазы одинаковы, то это означает, что они совпадают по фазе.

Синусоидальные напряжение и ток, графики которых представлены на рис. 2.3, описываются следующим образом:

u = U_msin(ωt + ψ_u); i = I_msin(ωt + ψ_i), (2.6)

причем угол сдвига фаз между током и напряжением (см. рис. 2.3) в этом случае φ = ψ_u - ψ_i.

Уравнения (2.6) можно записать иначе:

u = U_msin(ωt + ψ_i + φ); i = I_msin(ωt + ψ_u - φ),

поскольку ψ_u = ψ_i + φ и ψ_i = ψ_u - φ.

Из этих выражений следует, что напряжение опережает по фазе ток на угол φ (или ток отстает по фазе от напряжения на угол φ).