Х — значения переменной величины; р — частость; распределение: 1 — симметричное, 2 — левоасимметричное, 3 — правоасимметричное, 4 — крайнеасимметричное, 5 — гиперболоподобное
среднее квадратическое отклонение
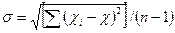 (V.26)
(V.26)
коэффициент вариации
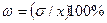 (V.27)
(V.27)
среднее абсолютное отклонение
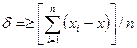 (V.28)
(V.28)
вероятное отклонение
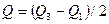 (V.29)
(V.29)
энтропия
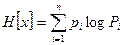 (V.30)
(V.30)
где xt — i-e значение признака; х — среднее арифметическое значение признака; Q1 — первый или нижний квартиль, т.е. значение признака, меньше которого в данной совокупности 1/4 всех значений; Q3 — верхний квартиль, т.е. значение признака, меньше которого 3/4 всех значений; п — общее число значений признака; Pi — вероятность (или частность, доля) значения xi.
Необходимо четко представлять, что энтропия и остальные числовые характеристики отражают разные стороны неоднородности. Покажем это на следующем условном примере.
Допустим, что имеются три совокупности образцов карбонатных пород. В 1-ю совокупность входят образцы с открытой пористостью 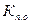 , имеющей только два различных значения, во 2-ю — образцы с пористостью, принимающей четыре разных значения, и в 3-ю — шесть разных значений.
, имеющей только два различных значения, во 2-ю — образцы с пористостью, принимающей четыре разных значения, и в 3-ю — шесть разных значений.
Примем, что в каждой совокупности количество образцов с одинаковыми значениями пористости равно, т.е. равны относительные частоты таких образцов. Пусть также во всех трех совокупностях будут одни и те же интервалы изменения
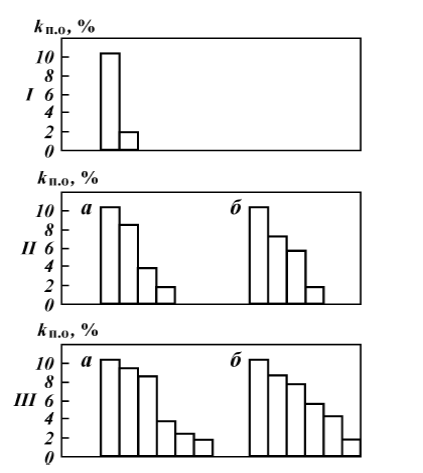
Рис. 31. Соотношение значений пористости 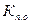 образцов трех совокупностей:
образцов трех совокупностей:
/, II, III — совокупности соответственно с двумя, четырьмя и шестью значениями пористости: а и б — варианты соотношения пористости во 2-й и 3-й совокупностях
пористости (т.е. размах R) и среднее значение 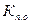 ; R = 8;
; R = 8; 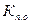 = 6. Характеристики всех трех совокупностей с возможными вариантами (а и б) приведены на рис. 31 ив табл. 3.
= 6. Характеристики всех трех совокупностей с возможными вариантами (а и б) приведены на рис. 31 ив табл. 3.
От 1-й совокупности к 3-й σ 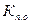 и ω
и ω 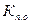 убывают, а Н(
убывают, а Н( 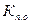 ) возрастает.
) возрастает.
Таблица 3
Дата добавления: 2015-10-19; просмотров: 1037;
