Реляционная модель данных. Реляционная модель данных (РМД) – это способ рассмотрения данных, при котором данные воспринимаются пользователем как взаимосвязанные таблицы и в распоряжении
Реляционная модель данных (РМД) – это способ рассмотрения данных, при котором данные воспринимаются пользователем как взаимосвязанные таблицы и в распоряжении пользователя имеются некоторые операторы, которые генерируют новые таблицы из старых.
Основной структурой данных в РМД является отношение (от англ. relation – отношение). Под отношениями (таблицами) здесь понимается структура данных, состоящая из строк (кортежей) и столбцов. В этой структуре каждый столбец содержит данные только одного типа, каждая строка состоит из набора значений составляющих ее столбцов.
Символическое отношение записывается в виде R(А1, А2,..., Аk).
Пример информационного отношения R (ФИО, Адрес, Телефон):
| ФИО | Адрес | Телефон |
| Иванов А.А. | ул. Некрасова,12 | 12-23-34 |
| Петров В.В. | ул. Гончарова, 4 | 23-45-56 |
| Сидоров М.М. | ул. Островского, 24 | 56-89-45 |
Т. о.реляционная модель данных характеризуется следующими компонентами:
· информационной конструкцией – отношением с двухуровневой структурой;
· допустимыми операциями над отношениями;
· ограничениями – функциональными зависимостями между атрибутами отношения.
Рассмотрим операции, которые могут быть произведены над отношениями. Как правило, в перечень включаются следующие операции: объединение, пересечение, вычитание, проекция, произведение, ограничение, соединение, деление и выборка.
Объединение, пересечение и вычитание – бинарные операции, выполняемые над двумя отношениями - синонимами. Синонимами называются отношения R1 и R2 с одинаковым порядком n, если для атрибута Ai (i = 1…n) из отношения R1 найдется атрибут Вj (j = 1…n) из R2, такой, что значения Ai и Bj принадлежат общей области определения. Атрибуты Ai и Bj обладающиеэтим свойством, называются ролевыми.
Объединение T = R1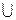 
R2 является отношением того же порядка, строки которого принадлежат или R1, или R2, или им обоим. Пересечение Т = R1 ∩ R2 состоит из строк, принадлежащих R1 и R2 одновременно. Вычитание Т= R1 \ R2 содержит строки из R1, отсутствующие в R2.
Проекцией называется операция, которая переносит в результирующее отношение столбцы исходного отношения, указанные в условии операции. Из результирующего отношения исключаются некоторые строки, чтобы соблюдалось условие о несовпадении значений строк. Алгебраическая запись проекции имеет вид:
T = R [L],
где R – исходное отношение;
T - результирующее отношение;
L – условие проекции (список атрибутов отношения Т).
Операция выборки. Для значений атрибутов отношения R формулируются условия вида
<имя атрибута>Q<значение атрибута>,
где Q= {=, ¹, >, <, ³, £}.
Эти условия могут связываться вместе с помощью логических операций Ù (и) Ú (или) в общее условие выборки. Операция выборки обозначается следующим образом:
Т = R [условие выборки]
где Т –результат выборки. Отношение Т содержит такие строки из R, которые удовлетворяют условию выборки.
Произведение двух отношений R и S в реляционной алгебре определяется следующим образом. Строки отношения Т=R Ä S образуются путем сцепления во всех возможных сочетаниях строк первого отношения ri со строками второго sj. Сцепление означает, что строка ri из n элементов и строка sj из m элементов образуют новую строку длиной n+m, в которой сначала располагаются элементы из ri, а затем - из sj.
Операция ограничения определена на одном отношении R. В этом отношении должны быть выделены два непересекающихся списка атрибутов одинаковой длины M1 =(А1, À2,…., Ak) и М2 = (В1, В2,..., Bk). M1 и М2 должны являться синонимами. Между кортежами таблиц r1(M1) и r2(M2) устанавливается бинарное отношение Q = {=, ¹, >, <., £, ³}. Если i-я строка из r1 и i-я строка из r2 удовлетворяют отношению Q, то i-я строка отношения R остается в нем после выполнения операции ограничения. Это условие проверяется для всех строк.
Алгебраическая запись ограничения имеет вид:
Т = R [M1 Q M2],
где Т - имя отношения, получаемогов результате ограничения.
Операция соединения представляет собой связку операций произведения и ограничения и определяется с помощью тождества:
Т = R [M1 Q M2] S = (R Ä S) [M1 Q M2],
где M1 - список атрибутов из R,
М2 - синонимичный список атрибутов из S.
Частным случаем операции соединения является натуральное соединение (или эквисоединение). Для эквисоединения Т = R><S в качестве отношения Q используется только равенство, множества имен атрибутов М1 и М2 должны содержать все пары ролевых атрибутов, принадлежащие R и S соответственно, в результате эквисоединения столбцы с именами из М2 подавляются.
Операция деления рассматривает произвольное отношение R (делитель) как бинарное. Для этого все атрибуты разделяются на два непересекающихся подмножества М и М'. Для каждой строки ri таблицы r(М) вводится операция «образ», результатом которой являются строки rj Î r(М'), такие, что пара (ri, rj,) принадлежит отношению R. Операция «образ» обозначается как im(ri)={rj1',rj2¢, .... rjk'}.
Отношение-делитель S должно быть синонимом для r(М). Операция деления сводится к вычислению образов всех строк делителя S и формированию пересечения этих образов. Результат деления является подмножеством строк таблицы r(М).
Алгебраическая запись деления имеет вид:
Т = R[М¸N] S,
где N - список атрибутов отношения S.
Дата добавления: 2015-10-19; просмотров: 776;